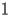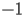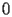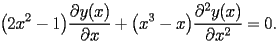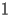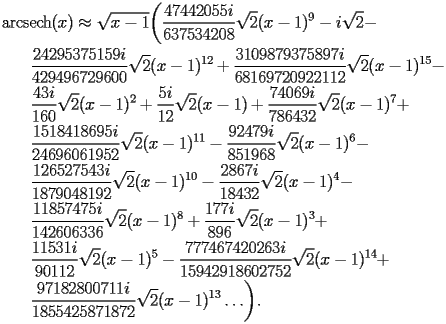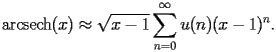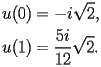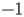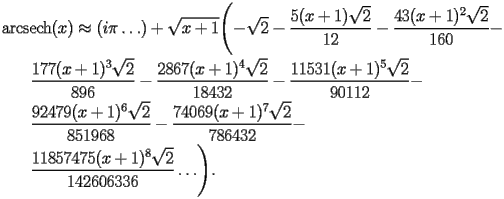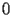HASC Inverse Hyperbolic Secant

HASC.1 Introduction

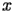Let $x$ be a complex variable of 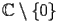$\mathbb{C} \setminus \{0\}$ .The function Inverse Hyperbolic Secant (noted 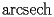$\operatorname{arcsech}$ ) is defined by the following second order differential equation

$\begin{equation*} \begin{split} \bigl(2 x^{2} - 1\bigr) \frac{\partial y (x)}{\partial x} + \bigl(x^{3} - x\bigr) \frac{\partial^{2} y (x)}{\partial x^{2}}& =0. \end{split} \end{equation*}$

HASC.1.1

The initial conditions of HASC.1.1 at 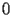$0$ are not simple to state, since 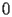$0$ is a (regular) singular point.

Related functions: Inverse Secant,Inverse Cosecant

HASC.2 Series and asymptotic expansions

top up back next into bottom

HASC.2.1 Asymptotic expansion at

top up back next into bottom

HASC.2.1.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{arcsech} (x)\approx \sqrt{x - 1} \biggl(\frac{47442055 i}{637534208} \sqrt{2} (x - 1)^{9} - i \sqrt{2} - \\ & \quad{}\quad{}\frac{24295375159 i}{429496729600} \sqrt{2} (x - 1)^{12} + \frac{3109879375897 i}{68169720922112} \sqrt{2} (x - 1)^{15} - \\ & \quad{}\quad{}\frac{43 i}{160} \sqrt{2} (x - 1)^{2} + \frac{5 i}{12} \sqrt{2} (x - 1) + \frac{74069 i}{786432} \sqrt{2} (x - 1)^{7} + \\ & \quad{}\quad{}\frac{1518418695 i}{24696061952} \sqrt{2} (x - 1)^{11} - \frac{92479 i}{851968} \sqrt{2} (x - 1)^{6} - \\ & \quad{}\quad{}\frac{126527543 i}{1879048192} \sqrt{2} (x - 1)^{10} - \frac{2867 i}{18432} \sqrt{2} (x - 1)^{4} - \\ & \quad{}\quad{}\frac{11857475 i}{142606336} \sqrt{2} (x - 1)^{8} + \frac{177 i}{896} \sqrt{2} (x - 1)^{3} + \\ & \quad{}\quad{}\frac{11531 i}{90112} \sqrt{2} (x - 1)^{5} - \frac{777467420263 i}{15942918602752} \sqrt{2} (x - 1)^{14} + \\ & \quad{}\quad{}\frac{97182800711 i}{1855425871872} \sqrt{2} (x - 1)^{13}\ldots\biggr). \end{split} \end{equation*}$

HASC.2.1.1.1

HASC.2.1.2 General form

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{arcsech} (x)\approx \sqrt{x - 1} \sum_{n = 0}^{\infty} u (n) (x - 1)^{n}. \end{split} \end{equation*}$

HASC.2.1.2.1

The coefficients $u (n)$

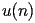satisfy the recurrence

$\begin{equation*} \begin{split} & 2 u (n) \biggl(\frac{1}{2} + n\biggr) n + u (n - 1) \biggl(-\frac{1}{2} + n\biggr) \biggl(-\frac{1}{2} + 3 n\biggr) + u (n - 2) \biggl(-\frac{3}{2} + n\biggr) \biggl(-\frac{1}{2} + n\biggr) \\ & \quad{}\quad{}=0. \end{split} \end{equation*}$

HASC.2.1.2.2

Initial conditions of HASC.2.1.2.2 are given by

$\begin{equation*} \begin{split} u (0)& =-i\sqrt{2}, \\ u (1)& =\frac{5 i}{12} \sqrt{2}. \end{split} \end{equation*}$

HASC.2.1.2.3

HASC.2.2 Asymptotic expansion at

top up back next into bottom

HASC.2.2.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{arcsech} (x)\approx (i \pi\ldots) + \sqrt{x + 1} \Biggl(-\sqrt{2} - \frac{5 (x + 1) \sqrt{2}}{12} - \frac{43 (x + 1)^{2} \sqrt{2}}{160} - \\ & \quad{}\quad{}\frac{177 (x + 1)^{3} \sqrt{2}}{896} - \frac{2867 (x + 1)^{4} \sqrt{2}}{18432} - \frac{11531 (x + 1)^{5} \sqrt{2}}{90112} - \\ & \quad{}\quad{}\frac{92479 (x + 1)^{6} \sqrt{2}}{851968} - \frac{74069 (x + 1)^{7} \sqrt{2}}{786432} - \\ & \quad{}\quad{}\frac{11857475 (x + 1)^{8} \sqrt{2}}{142606336}\ldots\Biggr). \end{split} \end{equation*}$