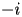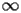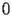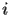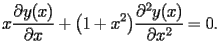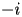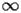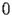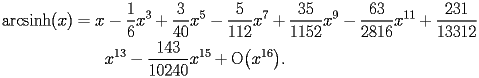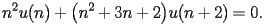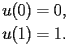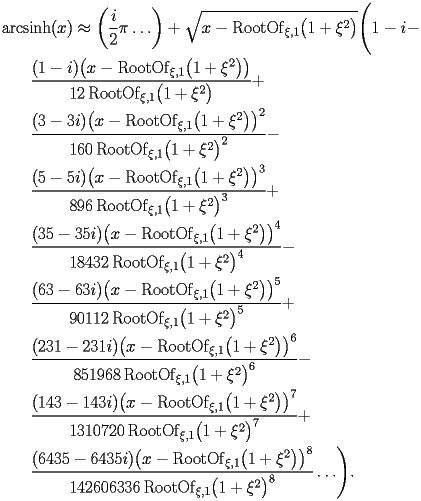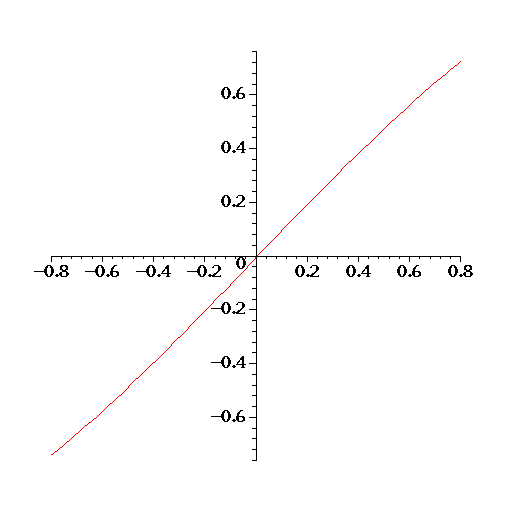HASN Inverse Hyperbolic Sine

HASN.1 Introduction

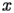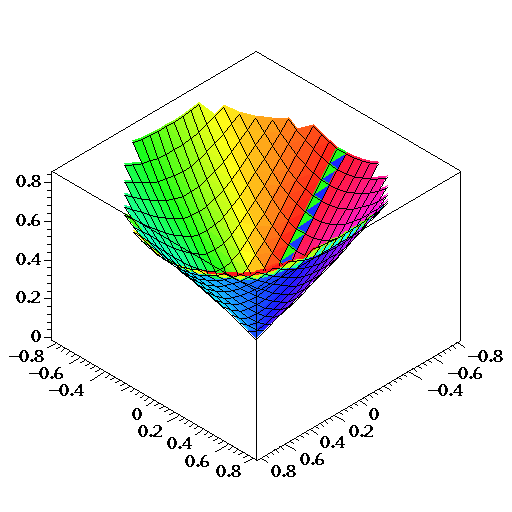
Let $x$ be a complex variable of 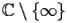$\mathbb{C} \setminus \{\infty\}$ .The function Inverse Hyperbolic Sine (noted 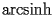$\operatorname{arcsinh}$ ) is defined by the following second order differential equation

$\begin{equation*} \begin{split} x \frac{\partial y (x)}{\partial x} + \bigl(1 + x^{2}\bigr) \frac{\partial^{2} y (x)}{\partial x^{2}}& =0. \end{split} \end{equation*}$

HASN.1.1

The initial conditions of HASN.1.1 are given at $0$ by

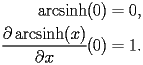
$\begin{equation*} \begin{split} \operatorname{arcsinh} (0)& =0, \\ \frac{\partial \operatorname{arcsinh} (x)}{\partial x} (0)& =1. \end{split} \end{equation*}$

HASN.1.2

HASN.2 Series and asymptotic expansions

top up back next into bottom

HASN.2.1 Asymptotic expansion at

top up back next into bottom

HASN.2.1.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{arcsinh} (x)\approx \biggl(-\frac{i}{2}\pi\ldots\biggr) + \sqrt{x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)} \Biggl(1 + i - \\ & \quad{}\quad{}\frac{(1 + i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)}{12 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)} + \\ & \quad{}\quad{}\frac{(3 + 3 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{2}}{160 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{2}} - \\ & \quad{}\quad{}\frac{(5 + 5 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{3}}{896 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{3}} + \\ & \quad{}\quad{}\frac{(35 + 35 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{4}}{18432 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{4}} - \\ & \quad{}\quad{}\frac{(63 + 63 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{5}}{90112 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{5}} + \\ & \quad{}\quad{}\frac{(231 + 231 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{6}}{851968 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{6}} - \\ & \quad{}\quad{}\frac{(143 + 143 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{7}}{1310720 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{7}} + \\ & \quad{}\quad{}\frac{(6435 + 6435 i) \bigl(x - \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)\bigr)^{8}}{142606336 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{8}}\ldots\Biggr). \end{split} \end{equation*}$

HASN.2.1.1.1

HASN.2.1.2 General form

top up back next into bottom

The general form of is not easy to state and requires to exhibit the basis of formal solutions of ?? (coming soon).

HASN.2.2 Asymptotic expansion at $\infty$

top up back next into bottom

HASN.2.2.1 First terms

top up back next into bottom

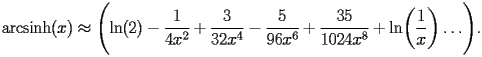
$\begin{equation*} \begin{split} & \operatorname{arcsinh} (x)\approx \Biggl(\operatorname{ln} (2) - \frac{1}{4 x^{2}} + \frac{3}{32 x^{4}} - \frac{5}{96 x^{6}} + \frac{35}{1024 x^{8}} + \operatorname{ln} \biggl(\frac{1}{x}\biggr)\ldots\Biggr). \end{split} \end{equation*}$

HASN.2.2.1.1

HASN.2.2.2 General form

top up back next into bottom

The general form of is not easy to state and requires to exhibit the basis of formal solutions of ?? (coming soon).

HASN.2.3 Taylor expansion at

top up back next into bottom

HASN.2.3.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} \operatorname{arcsinh} (x)& =x - \frac{1}{6} x^{3} + \frac{3}{40} x^{5} - \frac{5}{112} x^{7} + \frac{35}{1152} x^{9} - \frac{63}{2816} x^{11} + \frac{231}{13312} \\ & \quad{}\quad{}x^{13} - \frac{143}{10240} x^{15} + \operatorname{O} \bigl(x^{16}\bigr). \end{split} \end{equation*}$

HASN.2.3.1.1

HASN.2.3.2 General form

top up back next into bottom

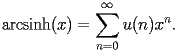
$\begin{equation*} \begin{split} \operatorname{arcsinh} (x)& =\sum_{n = 0}^{\infty} u (n) x^{n}. \end{split} \end{equation*}$

HASN.2.3.2.1

The coefficients $u (n)$

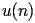satisfy the recurrence

$\begin{equation*} \begin{split} n^{2} u (n) + \bigl(n^{2} + 3 n + 2\bigr) u (n + 2)& =0. \end{split} \end{equation*}$

HASN.2.3.2.2

Initial conditions of HASN.2.3.2.2 are given by

$\begin{equation*} \begin{split} u (0)& =0, \\ u (1)& =1. \end{split} \end{equation*}$

HASN.2.3.2.3

HASN.2.4 Asymptotic expansion at

top up back next into bottom

HASN.2.4.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{arcsinh} (x)\approx \biggl(\frac{i}{2} \pi\ldots\biggr) + \sqrt{x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)} \Biggl(1 - i - \\ & \quad{}\quad{}\frac{(1 - i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)}{12 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)} + \\ & \quad{}\quad{}\frac{(3 - 3 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{2}}{160 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{2}} - \\ & \quad{}\quad{}\frac{(5 - 5 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{3}}{896 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{3}} + \\ & \quad{}\quad{}\frac{(35 - 35 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{4}}{18432 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{4}} - \\ & \quad{}\quad{}\frac{(63 - 63 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{5}}{90112 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{5}} + \\ & \quad{}\quad{}\frac{(231 - 231 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{6}}{851968 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{6}} - \\ & \quad{}\quad{}\frac{(143 - 143 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{7}}{1310720 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{7}} + \\ & \quad{}\quad{}\frac{(6435 - 6435 i) \bigl(x - \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)\bigr)^{8}}{142606336 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{8}}\ldots\Biggr). \end{split} \end{equation*}$

HASN.2.4.1.1

HASN.2.4.2 General form

top up back next into bottom

The general form of is not easy to state and requires to exhibit the basis of formal solutions of ?? (coming soon).

HASN.3 Graphs

top up back next into bottom

HASN.3.1 Real axis

top up back next into bottom

HASN.3.2 Complex plane

top up back next into bottom