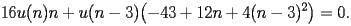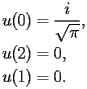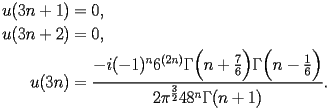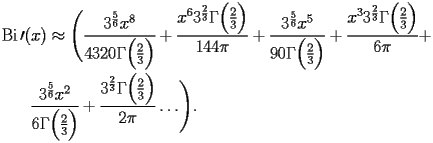DBI Derivative of Airy Bi

DBI.1 Introduction

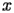Let $x$ be a complex variable of 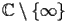$\mathbb{C} \setminus \{\infty\}$ .The function Derivative of Airy Bi (noted 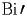$\operatorname{Bi} \prime$ ) is defined by the following second order differential equation

$\begin{equation*} \begin{split} -x^{2} y (x) - \frac{\partial y (x)}{\partial x} + x \frac{\partial^{2} y (x)}{\partial x^{2}}& =0. \end{split} \end{equation*}$

DBI.1.1

Although 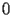$0$ is a singularity of DBI.1.1, the initial conditions can be given by

$\begin{equation*} \begin{split} [1] \operatorname{Bi} \prime (x)& =\frac{3^{\frac{2}{3}} \Gamma \Bigl(\frac{2}{3}\Bigr)}{2 \pi}, \\ \bigl[x^{2}\bigr] \operatorname{Bi} \prime (x)& =\frac{3^{\frac{5}{6}}}{6 \Gamma \Bigl(\frac{2}{3}\Bigr)}. \end{split} \end{equation*}$

DBI.1.2

Related function: Derivative of Airy Ai

DBI.2 Series and asymptotic expansions

top up back next into bottom

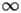
DBI.2.1 Asymptotic expansion at $\infty$

top up back next into bottom

DBI.2.1.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{Bi} \prime (x)\approx \frac{\operatorname{e} ^{\Bigl(\frac{-2}{3 \xi^{3}}\Bigr)} \biggl(\frac{i}{\sqrt{\pi}} + \frac{7 i \xi^{3}}{48 \sqrt{\pi}} + \ldots\biggr)}{\sqrt{\xi}} \end{split} \end{equation*}$

where $\xi = -\sqrt{\frac{1}{x}}$

DBI.2.1.2 General form

top up back next into bottom

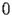
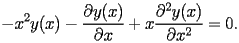
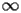
$\begin{equation*} \begin{split} & \operatorname{Bi} \prime (x)\approx \frac{\operatorname{e} ^{\Bigl(\frac{-2}{3 \xi^{3}}\Bigr)} \sum_{n = 0}^{\infty} u (n) \xi^{n}}{\sqrt{\xi}} \end{split} \end{equation*}$

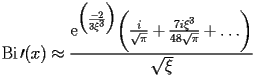
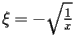
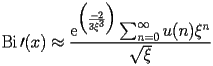
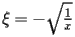where $\xi = -\sqrt{\frac{1}{x}}$ The coefficients $u (n)$

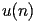satisfy the following recurrence

$\begin{equation*} \begin{split} 16 u (n) n + u (n - 3) \bigl(-43 + 12 n + 4 (n - 3)^{2}\bigr)& =0. \end{split} \end{equation*}$

whose initial conditions are given by

$\begin{equation*} \begin{split} u (0)& =\frac{i}{\sqrt{\pi}}, \\ u (2)& =0, \\ u (1)& =0. \end{split} \end{equation*}$

This recurrence has the closed form solution

$\begin{equation*} \begin{split} u (3 n + 1)& =0, \\ u (3 n + 2)& =0, \\ u (3 n)& =\frac{-i(-1)^{n} 6^{(2 n)} \Gamma \Bigl(n + \frac{7}{6}\Bigr) \Gamma \Bigl(n - \frac{1}{6}\Bigr)}{2 \pi^{\frac{3}{2}} 48^{n} \Gamma (n + 1)}. \end{split} \end{equation*}$

DBI.2.2 Asymptotic expansion at

top up back next into bottom

DBI.2.2.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{Bi} \prime (x)\approx \Biggl(\frac{3^{\frac{5}{6}} x^{8}}{4320 \Gamma \Bigl(\frac{2}{3}\Bigr)} + \frac{x^{6} 3^{\frac{2}{3}} \Gamma \Bigl(\frac{2}{3}\Bigr)}{144 \pi} + \frac{3^{\frac{5}{6}} x^{5}}{90 \Gamma \Bigl(\frac{2}{3}\Bigr)} + \frac{x^{3} 3^{\frac{2}{3}} \Gamma \Bigl(\frac{2}{3}\Bigr)}{6 \pi} + \\ & \quad{}\quad{}\frac{3^{\frac{5}{6}} x^{2}}{6 \Gamma \Bigl(\frac{2}{3}\Bigr)} + \frac{3^{\frac{2}{3}} \Gamma \Bigl(\frac{2}{3}\Bigr)}{2 \pi}\ldots\Biggr). \end{split} \end{equation*}$

DBI.2.2.1.1

DBI.2.2.2 General form

top up back next into bottom

The general form of is not easy to state and requires to exhibit the basis of formal solutions of ?? (coming soon).