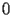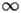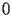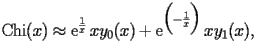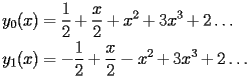CHI Hyperbolic Cosine Integral

CHI.1 Introduction

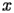Let $x$ be a complex variable of 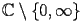$\mathbb{C} \setminus \{0,\infty\}$ .The function Hyperbolic Cosine Integral (noted 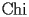$\operatorname{Chi}$ ) is defined by the following third order differential equation

$\begin{equation*} \begin{split} -x \frac{\partial y (x)}{\partial x} + 2 \frac{\partial^{2} y (x)}{\partial x^{2}} + x \frac{\partial^{3} y (x)}{\partial x^{3}}& =0. \end{split} \end{equation*}$

CHI.1.1

The initial conditions of CHI.1.1 at 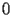$0$ are not simple to state, since 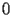$0$ is a (regular) singular point.

Related function: Hyperbolic Sine Integral

CHI.2 Series and asymptotic expansions

top up back next into bottom

CHI.2.1 Asymptotic expansion at

top up back next into bottom

CHI.2.1.1 First terms

top up back next into bottom

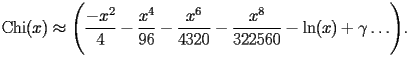
$\begin{equation*} \begin{split} & \operatorname{Chi} (x)\approx \Biggl(\frac{-x^{2}}{4} - \frac{x^{4}}{96} - \frac{x^{6}}{4320} - \frac{x^{8}}{322560} - \operatorname{ln} (x) + \gamma\ldots\Biggr). \end{split} \end{equation*}$

CHI.2.1.1.1

CHI.2.1.2 General form

top up back next into bottom

The general form of is not easy to state and requires to exhibit the basis of formal solutions of ?? (coming soon).

CHI.2.2 Asymptotic expansion at $\infty$

top up back next into bottom

CHI.2.2.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{Chi} (x)\approx \operatorname{e} ^{\frac{1}{x}} x y _{0} (x) + \operatorname{e} ^{\Bigl(-\frac{1}{x}\Bigr)} x y _{1} (x), \end{split} \end{equation*}$

where

$\begin{equation*} \begin{split} y _{0} (x)& =\frac{1}{2} + \frac{x}{2} + x^{2} + 3 x^{3} + 2 \ldots \\ y _{1} (x)& =-\frac{1}{2} + \frac{x}{2} - x^{2} + 3 x^{3} + 2 \ldots \end{split} \end{equation*}$

CHI.2.2.2 General form

top up back next into bottom

CHI.2.2.2.1 Auxiliary function $y _{0} (x)$

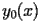
The coefficients $u (n)$

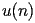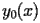of $y _{0} (x)$ satisfy the following recurrence

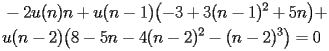
$\begin{equation*} \begin{split} & -2u (n) n + u (n - 1) \bigl(-3 + 3 (n - 1)^{2} + 5 n\bigr) + \\ & u (n - 2) \bigl(8 - 5 n - 4 (n - 2)^{2} - (n - 2)^{3}\bigr)=0 \end{split} \end{equation*}$

whose initial conditions are given by

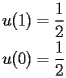
$\begin{equation*} \begin{split} u (1)& =\frac{1}{2} \\ u (0)& =\frac{1}{2} \end{split} \end{equation*}$

This recurrence has the closed form solution

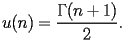
$\begin{equation*} \begin{split} u (n)& =\frac{\Gamma (n + 1)}{2}. \end{split} \end{equation*}$

CHI.2.2.2.2 Auxiliary function $y _{1} (x)$

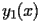
The coefficients $u (n)$

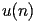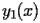of $y _{1} (x)$ satisfy the following recurrence

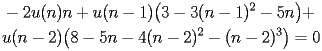
$\begin{equation*} \begin{split} & -2u (n) n + u (n - 1) \bigl(3 - 3 (n - 1)^{2} - 5 n\bigr) + \\ & u (n - 2) \bigl(8 - 5 n - 4 (n - 2)^{2} - (n - 2)^{3}\bigr)=0 \end{split} \end{equation*}$

whose initial conditions are given by

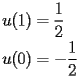
$\begin{equation*} \begin{split} u (1)& =\frac{1}{2} \\ u (0)& =-\frac{1}{2} \end{split} \end{equation*}$

This recurrence has the closed form solution

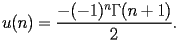
$\begin{equation*} \begin{split} u (n)& =\frac{-(-1)^{n} \Gamma (n + 1)}{2}. \end{split} \end{equation*}$