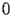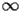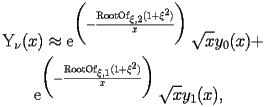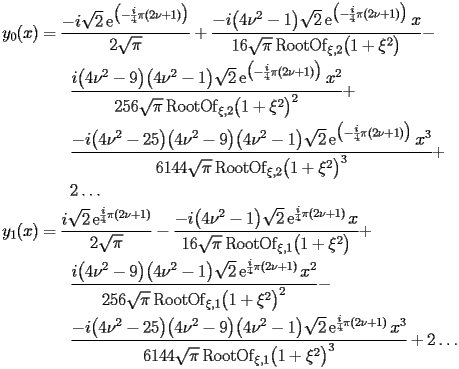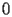BSY Bessel Y

BSY.1 Introduction

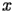Let $x$ be a complex variable of 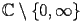$\mathbb{C} \setminus \{0,\infty\}$ and let 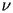$\nu$ denote a parameter (independent of 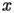$x$ ).The function Bessel Y (noted 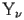$\operatorname{Y} _{\nu}$ ) is defined by the following second order differential equation

$\begin{equation*} \begin{split} \bigl(x^{2} - \nu^{2}\bigr) y (x) + x \frac{\partial y (x)}{\partial x} + x^{2} \frac{\partial^{2} y (x)}{\partial x^{2}}& =0. \end{split} \end{equation*}$

BSY.1.1

Although 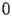$0$ is a singularity of BSY.1.1, the initial conditions can be given by

$\begin{equation*} \begin{split} \Bigl[x^{(-\nu)}\Bigr] \operatorname{Y} _{\nu} (x)& =-\frac{1}{\frac{\Gamma (-\nu + 1) \operatorname{sin} (\nu \pi)}{2^{\nu}}}, \\ \bigl[x^{\nu}\bigr] \operatorname{Y} _{\nu} (x)& =\frac{\operatorname{cos} (\nu \pi)}{\Gamma (\nu + 1) 2^{\nu} \operatorname{sin} (\nu \pi)}. \end{split} \end{equation*}$

BSY.1.2

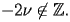
The formulae of this document are valid for $-2\nu \not\in \mathbb{Z} .$

Related functions: Hankel H1,Hankel H2,Bessel J

BSY.2 Series and asymptotic expansions

top up back next into bottom

BSY.2.1 Asymptotic expansion at $\infty$

top up back next into bottom

BSY.2.1.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{Y} _{\nu} (x)\approx \operatorname{e} ^{\biggl(-\frac{\operatorname{RootOf} _{\xi,2} (1 + \xi^{2})}{x}\biggr)} \sqrt{x} y _{0} (x) + \\ & \quad{}\quad{}\operatorname{e} ^{\biggl(-\frac{\operatorname{RootOf} _{\xi,1} (1 + \xi^{2})}{x}\biggr)} \sqrt{x} y _{1} (x), \end{split} \end{equation*}$

where

$\begin{equation*} \begin{split} y _{0} (x)& =\frac{-i\sqrt{2} \operatorname{e} ^{\bigl(-\frac{i}{4}\pi (2 \nu + 1)\bigr)}}{2 \sqrt{\pi}} + \frac{-i\bigl(4 \nu^{2} - 1\bigr) \sqrt{2} \operatorname{e} ^{\bigl(-\frac{i}{4}\pi (2 \nu + 1)\bigr)} x}{16 \sqrt{\pi} \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)} - \\ & \quad{}\quad{}\frac{i \bigl(4 \nu^{2} - 9\bigr) \bigl(4 \nu^{2} - 1\bigr) \sqrt{2} \operatorname{e} ^{\bigl(-\frac{i}{4}\pi (2 \nu + 1)\bigr)} x^{2}}{256 \sqrt{\pi} \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{2}} + \\ & \quad{}\quad{}\frac{-i\bigl(4 \nu^{2} - 25\bigr) \bigl(4 \nu^{2} - 9\bigr) \bigl(4 \nu^{2} - 1\bigr) \sqrt{2} \operatorname{e} ^{\bigl(-\frac{i}{4}\pi (2 \nu + 1)\bigr)} x^{3}}{6144 \sqrt{\pi} \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{3}} + \\ & \quad{}\quad{}2 \ldots \\ y _{1} (x)& =\frac{i \sqrt{2} \operatorname{e} ^{\frac{i}{4} \pi (2 \nu + 1)}}{2 \sqrt{\pi}} - \frac{-i\bigl(4 \nu^{2} - 1\bigr) \sqrt{2} \operatorname{e} ^{\frac{i}{4} \pi (2 \nu + 1)} x}{16 \sqrt{\pi} \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)} + \\ & \quad{}\quad{}\frac{i \bigl(4 \nu^{2} - 9\bigr) \bigl(4 \nu^{2} - 1\bigr) \sqrt{2} \operatorname{e} ^{\frac{i}{4} \pi (2 \nu + 1)} x^{2}}{256 \sqrt{\pi} \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{2}} - \\ & \quad{}\quad{}\frac{-i\bigl(4 \nu^{2} - 25\bigr) \bigl(4 \nu^{2} - 9\bigr) \bigl(4 \nu^{2} - 1\bigr) \sqrt{2} \operatorname{e} ^{\frac{i}{4} \pi (2 \nu + 1)} x^{3}}{6144 \sqrt{\pi} \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{3}} + 2 \ldots \end{split} \end{equation*}$

BSY.2.1.2 General form

top up back next into bottom

BSY.2.1.2.1 Auxiliary function $y _{0} (x)$

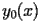
The coefficients $u (n)$

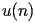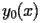of $y _{0} (x)$ satisfy the following recurrence

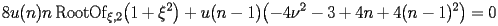
$\begin{equation*} \begin{split} & 8 u (n) n \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr) + u (n - 1) \bigl(-4\nu^{2} - 3 + 4 n + 4 (n - 1)^{2}\bigr)=0 \end{split} \end{equation*}$

whose initial conditions are given by

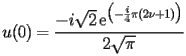
$\begin{equation*} \begin{split} u (0)& =\frac{-i\sqrt{2} \operatorname{e} ^{\bigl(-\frac{i}{4}\pi (2 \nu + 1)\bigr)}}{2 \sqrt{\pi}} \end{split} \end{equation*}$

This recurrence has the closed form solution

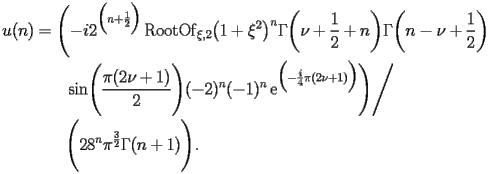
$\begin{equation*} \begin{split} u (n)& =\Biggl(-i2^{\Bigl(n + \frac{1}{2}\Bigr)} \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{n} \Gamma \biggl(\nu + \frac{1}{2} + n\biggr) \Gamma \biggl(n - \nu + \frac{1}{2}\biggr) \\ & \quad{}\quad{}\operatorname{sin} \Biggl(\frac{\pi (2 \nu + 1)}{2}\Biggr) (-2)^{n} (-1)^{n} \operatorname{e} ^{\Bigl(-\frac{i}{4}\pi (2 \nu + 1)\Bigr)}\Biggr)\Bigg/ \\ & \quad{}\quad{}\Biggl(2 8^{n} \pi^{\frac{3}{2}} \Gamma (n + 1)\Biggr). \end{split} \end{equation*}$

BSY.2.1.2.2 Auxiliary function $y _{1} (x)$

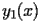
The coefficients $u (n)$

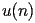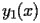of $y _{1} (x)$ satisfy the following recurrence

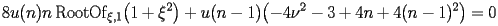
$\begin{equation*} \begin{split} & 8 u (n) n \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr) + u (n - 1) \bigl(-4\nu^{2} - 3 + 4 n + 4 (n - 1)^{2}\bigr)=0 \end{split} \end{equation*}$

whose initial conditions are given by

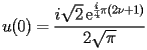
$\begin{equation*} \begin{split} u (0)& =\frac{i \sqrt{2} \operatorname{e} ^{\frac{i}{4} \pi (2 \nu + 1)}}{2 \sqrt{\pi}} \end{split} \end{equation*}$

This recurrence has the closed form solution

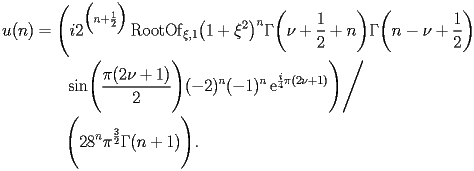
$\begin{equation*} \begin{split} u (n)& =\Biggl(i 2^{\Bigl(n + \frac{1}{2}\Bigr)} \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{n} \Gamma \biggl(\nu + \frac{1}{2} + n\biggr) \Gamma \biggl(n - \nu + \frac{1}{2}\biggr) \\ & \quad{}\quad{}\operatorname{sin} \Biggl(\frac{\pi (2 \nu + 1)}{2}\Biggr) (-2)^{n} (-1)^{n} \operatorname{e} ^{\frac{i}{4} \pi (2 \nu + 1)}\Biggr)\Bigg/ \\ & \quad{}\quad{}\Biggl(2 8^{n} \pi^{\frac{3}{2}} \Gamma (n + 1)\Biggr). \end{split} \end{equation*}$

BSY.2.2 Asymptotic expansion at

top up back next into bottom

BSY.2.2.1 First terms

top up back next into bottom

$\begin{equation*} \begin{split} & \operatorname{Y} _{\nu} (x)\approx \Biggl(-\frac{1}{\frac{\Gamma (-\nu + 1) \operatorname{sin} (\nu \pi)}{2^{\nu}}} - \frac{x^{2}}{\frac{4 (\nu - 1) \Gamma (-\nu + 1) \operatorname{sin} (\nu \pi)}{2^{\nu}}} - \\ & \quad{}\quad{}\frac{x^{4}}{\frac{32 (\nu - 1) (\nu - 2) \Gamma (-\nu + 1) \operatorname{sin} (\nu \pi)}{2^{\nu}}} - \\ & \quad{}\quad{}\frac{x^{6}}{\frac{384 (\nu - 1) (\nu - 2) (\nu - 3) \Gamma (-\nu + 1) \operatorname{sin} (\nu \pi)}{2^{\nu}}} - \\ & \quad{}\quad{}\frac{x^{8}}{\frac{6144 (\nu - 1) (\nu - 2) (\nu - 3) (\nu - 4) \Gamma (-\nu + 1) \operatorname{sin} (\nu \pi)}{2^{\nu}}}\ldots\Biggr)\Bigg/x^{\nu} + \\ & \quad{}\quad{}x^{\nu} \Biggl(\frac{\operatorname{cos} (\nu \pi)}{\Gamma (\nu + 1) 2^{\nu} \operatorname{sin} (\nu \pi)} - \frac{x^{2} \operatorname{cos} (\nu \pi)}{4 (\nu + 1) \Gamma (\nu + 1) 2^{\nu} \operatorname{sin} (\nu \pi)} \\ & \quad{}\quad{}+ \frac{x^{4} \operatorname{cos} (\nu \pi)}{32 (\nu + 1) (\nu + 2) \Gamma (\nu + 1) 2^{\nu} \operatorname{sin} (\nu \pi)} - \\ & \quad{}\quad{}\frac{x^{6} \operatorname{cos} (\nu \pi)}{384 (\nu + 1) (\nu + 2) (\nu + 3) \Gamma (\nu + 1) 2^{\nu} \operatorname{sin} (\nu \pi)} + \\ & \quad{}\quad{}\frac{x^{8} \operatorname{cos} (\nu \pi)}{6144 (\nu + 1) (\nu + 2) (\nu + 3) (\nu + 4) \Gamma (\nu + 1) 2^{\nu} \operatorname{sin} (\nu \pi)}\ldots\Biggr). \end{split} \end{equation*}$

BSY.2.2.1.1

BSY.2.2.2 General form

top up back next into bottom

The general form of is not easy to state and requires to exhibit the basis of formal solutions of ?? (coming soon).