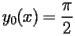SI Sine Integral
SI.1 Introduction |
top up back next into bottom |
Let
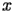 be a complex variable of
be a complex variable of
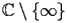 .The function Sine Integral (noted
.The function Sine Integral (noted
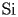 ) is defined by the following third order differential equation
) is defined by the following third order differential equation
| SI.1.1 |
Although
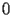 is a singularity of SI.1.1, the initial conditions can be given by
is a singularity of SI.1.1, the initial conditions can be given by
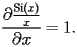
|
SI.1.2 |
Related function: Cosine Integral
SI.2 Series and asymptotic expansions |
top up back next into bottom |
SI.2.1 Asymptotic expansion at
|
top up back next into bottom |
SI.2.1.2 General form |
top up back next into bottom |
| SI.2.1.2.1 |
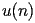 satisfy the recurrence
satisfy the recurrence
| SI.2.1.2.2 |
| SI.2.1.2.3 |
| SI.2.1.2.4 |
SI.2.2 Asymptotic expansion at
|
top up back next into bottom |
SI.2.2.2 General form |
top up back next into bottom |
SI.2.2.2.2 Auxiliary function
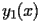
The coefficients
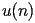 of
of
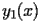 satisfy the following recurrence
satisfy the following recurrence

|
|
SI.2.2.2.3 Auxiliary function
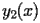
The coefficients
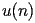 of
of
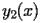 satisfy the following recurrence
satisfy the following recurrence
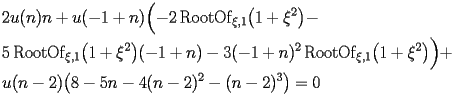
|
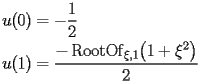
|
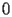
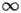
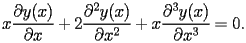

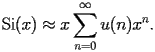
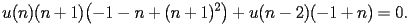
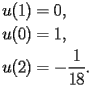
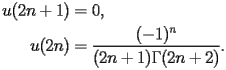
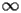
![\begin{equation*}
\begin{split}
& \operatorname{Si} (x)\approx ser _{\Bigl[1,1,\Bigl[\Bigl[0,\Bigl[\Bigl[0,\frac{\pi}{2}\Bigr]\Bigr]\Bigr]\Bigr]\Bigr]} + \operatorname{e} ^{\biggl(-\frac{\operatorname{RootOf} _{\xi,2} (1 + \xi^{2})}{x}\biggr)} x y _{1} (x) + \\
& \quad{}\quad{}\operatorname{e} ^{\biggl(-\frac{\operatorname{RootOf} _{\xi,1} (1 + \xi^{2})}{x}\biggr)} x y _{2} (x),
\end{split}
\end{equation*}](SI_17.gif)
![\begin{equation*}
\begin{split}
y _{0} (x)& =terms _{\Bigl[1,1,\Bigl[\Bigl[0,\Bigl[\Bigl[0,\frac{\pi}{2}\Bigr]\Bigr]\Bigr]\Bigr]\Bigr]} + \ldots \\
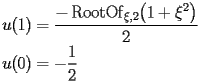
y _{1} (x)& =-\frac{1}{2} - \frac{\operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr) x}{2} - \\
& \quad{}\quad{}-\left(-\frac{1}{4} - \frac{5 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{2}}{4}\right) x^{2} - -\Biggl(-\operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr) + \\
& \quad{}\quad{}4 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr) \left(-\frac{1}{4} - \frac{5 \operatorname{RootOf} _{\xi,2} \bigl(1 + \xi^{2}\bigr)^{2}}{4}\right)\Biggr) x^{3} + 2 \ldots \\
y _{2} (x)& =-\frac{1}{2} - \frac{\operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr) x}{2} - \\
& \quad{}\quad{}-\left(-\frac{1}{4} - \frac{5 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{2}}{4}\right) x^{2} - -\Biggl(-\operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr) + \\
& \quad{}\quad{}4 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr) \left(-\frac{1}{4} - \frac{5 \operatorname{RootOf} _{\xi,1} \bigl(1 + \xi^{2}\bigr)^{2}}{4}\right)\Biggr) x^{3} + 2 \ldots
\end{split}
\end{equation*}](SI_18.gif)
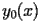
 has the exact form
has the exact form