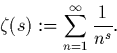
On explore ici quelques propriétés des séries de Dirichlet, lesquelles sont à la base de la théorie analytique des nombres. Seule l'inversion de Moebius, équation (3), est nécessaire à la Partie II du problème.
Q1. La fonction zeta de Riemann est définie par
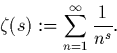
Établir (sans lourd détail analytique) la formule dite du produit Eulérien,
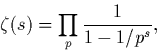 |
(1) |
Q2. Utiliser la question précédente pour établir par un argument tres simple d'analyse qu'il existe une infinité de nombres premiers. (Cette preuve ingénieuse du théorème d'Euclide est due à Euler.)
Note, Les propriétés fines de ![]() sont à la base du
théorème des nombres premiers (Riemann,
puis Hadamard et de la Vallée-Poussin)
d'après lequel
le nombre de nombres premiers inférieurs
à x, soit
sont à la base du
théorème des nombres premiers (Riemann,
puis Hadamard et de la Vallée-Poussin)
d'après lequel
le nombre de nombres premiers inférieurs
à x, soit ![]() , est estimé par:
, est estimé par:
| |
(2) |
En admettant (2), montrer que le nombre de premiers dont la représentation binaire comporte exactement n bits est asymptotique à
![]()
Q3. Montrer que
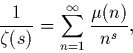
![]()
Q4. Soit ![]() une suite de complexes. On appelle
série génératrice de Dirichlet
associée à cette suite la somme
une suite de complexes. On appelle
série génératrice de Dirichlet
associée à cette suite la somme
![]()

En déduire la formule d'inversion de Moebius: pour deux suite fn,gn quelconques, on a l'équivalence
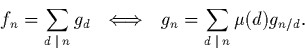 |
(3) |
Inverser la relation entre séries génératrices ordinaires:
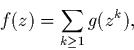
Q5. [Facultatif] Soit ![]() un système de fonctions.
Les cas
un système de fonctions.
Les cas
![]()
![]()
Pouvez-vous interpréter
![\begin{displaymath}[z^n]
\frac{1}{2-\frac{1}{1-z}},
~~~
[z^n]\frac{1}{2-e^z},~~~
[n^{-z}] \frac{1}{2-\zeta(z)},\end{displaymath}](img28.gif)
Cette partie du problème montre que des objets algébriques peuvent se traitent par les méthodes de la combinatoire énumérative. Les développements qui suivent sont à la base de l'analyse d'algorithmes probabilistes en calcul formel et en théorie des codes.
Rappel.
Pour un nombre premier p, on considère le corps F=Fp formé par les
entiers pris modulo p. On travaille dans l'anneau F[x] des polynômes
à
coefficients dans F. On rappelle que, dans cet anneau, il existe
une division euclidienne et une propriété de factorisation unique.
Les élements de F[x] qui sont indécomposables (l'équivalent
des nombres premiers) sont appelés polynômes irreductibles:
f est irréductible si ![]() implique g=1 ou h=1.
implique g=1 ou h=1.
Fixons p.
On désigne par ![]() la classe des polynômes unitaires
(dont le coefficient de tête vaut 1) et par
la classe des polynômes unitaires
(dont le coefficient de tête vaut 1) et par ![]() la
sous-classe des polynômes unitaires et irréductibles. Par
convention, la taille (au sens combinatoire) d'un polynôme est son
degré (au sens algébrique). La sous-classe
la
sous-classe des polynômes unitaires et irréductibles. Par
convention, la taille (au sens combinatoire) d'un polynôme est son
degré (au sens algébrique). La sous-classe ![]() représente
les polynômes unitaires ``sans carrés'', c-à-d, non divisibles
par un carré:
f est sans carré si
représente
les polynômes unitaires ``sans carrés'', c-à-d, non divisibles
par un carré:
f est sans carré si ![]() implique h=1.
implique h=1.
Q1.
Montrer que la série génératrice de ![]() vaut
vaut
![]()
Observer que tout ![]() s'écrit
s'écrit ![]() où g est sans carré et h quelconque. D'autre part,
sii
où g est sans carré et h quelconque. D'autre part,
sii ![]() est une classe de polynômes de série génératrice
H(z), la série génératrice de l'ensemble
est une classe de polynômes de série génératrice
H(z), la série génératrice de l'ensemble
![]() vaut H(z2).
En déduire la série génératrice de
vaut H(z2).
En déduire la série génératrice de ![]() .Calculer la probabilité qu'un polynôme pris uniformément
dans
.Calculer la probabilité qu'un polynôme pris uniformément
dans ![]() soit sans carré.
soit sans carré.
Q2. Montrer que
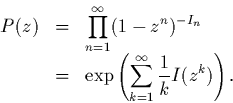
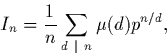
Q3. Montrer brièvement que
![]()
On suppose qu'on dispose de deux procédures:
draw(n) tire au hasard un élément de ![]() et irred(f) répond vrai ou faux selon que f est irréductible ou non.
et irred(f) répond vrai ou faux selon que f est irréductible ou non.
Combien d'essais en moyenne effectue l'algorithme de tirage d'un polynôme irréductible suivant?
repeat
f := draw(n);
until irred(f);
Quelle est la variance du nombre de tirages?
Q4.
Soit ![]() le nombre de facteurs irréductibles de
f comptés avec multiplicité, par exemple,
le nombre de facteurs irréductibles de
f comptés avec multiplicité, par exemple,
![]()
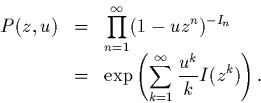
Montrer que l'espérance de ![]() prise sur l'ensemble des
polynômes
prise sur l'ensemble des
polynômes ![]() vaut exactement
vaut exactement
![\begin{displaymath}
M_n=\hbox{coeff} [z^n]\, \left(\frac{\partial}{\partial u}P\left(\frac
zp ,u\right)\right)_{u=1}. \end{displaymath}](img53.gif)
![\begin{displaymath}[z^n]
\left(I(\frac{z}{p})+I(\frac{z^2}{p^2})+I(\frac{z^3}{p^3})+\cdots\right)\end{displaymath}](img54.gif)
![]()
[Facultatif] Qu'est-ce que ce résultat suggère
quant au nombre moyen de facteurs premiers d'un entier ![]() ?
?
Q5. [Facultatif] Montrer que le nombre d'éléments de ![]() qui ont n1 facteurs irréductibles de degré 1, n2 de
degré 2, etc, vaut (en marquant la dépendance en p):
qui ont n1 facteurs irréductibles de degré 1, n2 de
degré 2, etc, vaut (en marquant la dépendance en p):
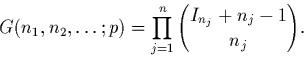
![]()
Montrer que ![]() est aussi le nombre de permutations de n
qui ont n1 cycles de taille 1, n2 cycles de taille 2, etc.
En résumé la décomposition en facteurs irréductibles d'un polynôme
de degre fixé n sur un corps de grande cardinalité ressemble à
la décomposition en cycles d'une permutation de la même taille n.
est aussi le nombre de permutations de n
qui ont n1 cycles de taille 1, n2 cycles de taille 2, etc.
En résumé la décomposition en facteurs irréductibles d'un polynôme
de degre fixé n sur un corps de grande cardinalité ressemble à
la décomposition en cycles d'une permutation de la même taille n.
Il s'agit là d'un exercice à préparer en binome. Le résultat peut fort bien être une feuille de travail MAPLE, mais éditée convenablement et brièvement commentée, ou bien un ``compte-rendu'' d'expérience manuscrit.
Le problème traité ici est une simplification d'une situation qui s'est présentée réellement il y a quelques années. Les statisticiens construisent des arbres de classification appelés hiérarchies. Le problème consiste à analyser les propriétés des hiérarchies aléatoires sur la base du principe qu'une classification produite dans le monde réel (par ex. par un programme d'analyse statistique) a d'autant plus de ``chances'' d'être significative qu'elle s'écarte des lois du hasard. D'où l'intérêt de quantifier l'aléa!
Les hiérarchies sont des arbres dont les sommets externes sont les
n objets à
classifier (la taille vaut alors n) et dont les sommets internes
(représentant les ``classes'') ont
degré tous ![]() , car il faut que la classification soit non triviale.
Par exemple:
, car il faut que la classification soit non triviale.
Par exemple:
C=chat, H=homme, L=lion, O=orang-outang, T=tigre, V=vache
. n = 5 (nombre de sommets externes)
/|\
/ | \ 3 sommets internes (classes)
. V .
/|\ /\
T C L H O
Les hiérarchies sont donc ``non-planaires'' (pas de distinction
gauche/droite) et enracinées,
de par l'origine du problème. Les objets à classifier sont
assimilés aux étiquettes ![]() .En d'autres termes:
.En d'autres termes:
La classeSymboliquement:des hiérarchies est la classe des arbres enracinés non-planaires, étiquetés aux sommets externes seulement (qui déterminent la taille) et dont les sommets internes ont tous degrés
.
![]()
III.1 Dénombrement asymptotique des hiérarchies
Q1. On commence par se convaincre que la série génératrice exponentielle des hierarchies vérifie l'équation
![]()
z=WeW.
définie et positive pour
eqH:=H=z+exp(H)-1-H; Hz:=solve(eqH,H);
Calculer les 30 premiers coefficients
Hs:=series(Hz,z=0,31);
for i from 0 to 30 do
c[i]:=coeff(Hs,z,i)*1.0 od;
et deviner une loi très approximative de croissance de
![]()
plot([seq([i,c[i+1]/c[i]],i=5..30)],0..30,0..3);
Le nombre de hiérarchies de taille n vaut Hn=n!cn.
Q2. On sait que le rayon de convergence d'une série entière à coefficients positifs est égal à la distance entre l'origine et la singularité positive la plus proche. Ici, la singularité correspond à une pente verticale (de dérivée infinie), comme on peut s'en convaincre par un plot.
plot(Hz,z=0..0.5); plot(diff(Hz,z),z=0..0.5);
H1z:=normal(diff(Hz,z));
Par une suite de tracés de ce type, on devra obtenir une
approximation à 0.001 près de la singularité positive,
![]()
Combien de chiffres environ comporte la représentation décimale de H1000?
Q3. On se propose de déterminer maintenant exactement la
singularité positive ![]() . En supposant qu'elle provient de
l'annulation du denominateur de
. En supposant qu'elle provient de
l'annulation du denominateur de ![]() ,on déterminera alors sa valeur exacte (utliser solve):
,on déterminera alors sa valeur exacte (utliser solve):
![]()
On peut alors tenter de comprendre de quelle manière H(z) devient
singulière lorsque z tend vers ![]() par valeurs inférieures.
Il est commode de poser
par valeurs inférieures.
Il est commode de poser ![]() et faire
et faire ![]() ,ce qui s'obtient par un développement en série.
,ce qui s'obtient par un développement en série.
map(simplify,series(subs(z=rho-h,Hz),h=0));
On suppose que cn est asymptotiquement equivalent a ce que l'on obtient en ne retenant que les deux premiers termes, soit
![]()
![]()
Vérifier comme suit:
for i from 2 to 30 do
evalf(coeff(Hs,z,i)/rho^(-i+1/2)*i^(3/2)*sqrt(Pi))
od;
Avec quelle précision estimez-vous pouvoir prévoir la valeur de
H1000?
III.2 Nombre d'étapes de classification. On s'intéresse au nombre de sommets internes de l'arbre (le nombre de classes). Soient Hn,k le nombre de hiérarchies de taille n ayant k sommets internes et n sommets externes. On se convaincra (ou bien, on admettra) que la série double
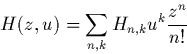
![]()
Q4. Résoudre cette équation en termes de la fonction W de Lambert. On pose
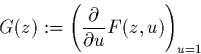
Soit dn:=[zn]G(z), de sorte que le nombre moyen de sommets internes dans une hiérarchie de taille n vaut
![]()
Deviner une formule approximative décrivant la croissance
asymptotique de ![]() .
.
Chercher a améliorer l'estimation, empiriquement (en devinant simultanément une valeur approchée du terme d'erreur), et/ou en évaluant
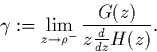
Estimer au mieux ![]() .
.
Un programme de classification produit sur n=1000 données une hierarchie qui comprend 273 classes (sommets internes). La hiérarchie ainsi constituée ressemble-t-elle à une hiérarchie aléatoire?
[ ] OUI [ ] NON [ ] INCERTAIN
Philippe Flajolet
1/17/1999