 Cliquer ici
pour envoyer un courrier à tous.
Cliquer ici
pour envoyer un courrier à tous.
Horaires.
Allez a Bordeaux!.
Je voudrais juste signaler a ceux d'entre vous pour qui ca ne poserait
pas de probleme
de conflit de dates un interessant ensemble de manifestations a
Bordeaux qui sont etroitement liees
aux themes du DEA. Il s'agit de
(On peut choisir a la carte parmi 1,2,3).
Un point d'entree Web possible est
http://pauillac.inria.fr/algo/AofA/Alea/index.html
Probleme. Distribue' le 20 janvier 1999, il fut du^ quatorze jours plus tard, soit le 3 fevrier 1999. Le texte est encore depose' ici:
Poly. Le poly du cours est constitue des Chapitres 1 a 5 du futur livre Flajolet-Sedgewick, Analytic Combinatorics. Ceci est disponible sur le Web:
Enseignants. Étudiants.
 Cliquer ici
pour envoyer un courrier à tous.
Cliquer ici
pour envoyer un courrier à tous.
Cours 1 [9 decembre 1998].
Cours 2 [16 decembre 1998].
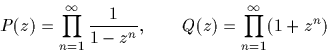
 Cliquer ici!
Cliquer ici!
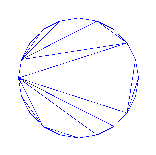
Cours 3 [6 Janvier 1999]
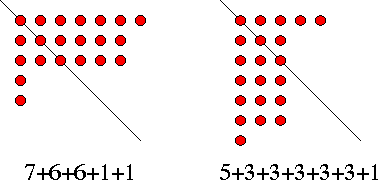
Les monotonies sont une illustration. On s'interesse depuis
longtemps aux grandes
sequences de chance ou de malchance dans les jeux de hasard.
Soit L[k] le langage des mots qui ont moins de k
lettres b consecutives. Alors L[k]=(ab<k).(ab<k)*,
d'apres la scansion qui precede. ici, b<k=1+b+bb+...+b^{k-1}.
D'ou la serie generatrice (1-z^k)/(1-2z+z^(k+1)).
Knuth (1978) a etudie' ces fraction rationnelles dont les poles
dominants s'accumulent en 1/2. Il a montre' notamment
ainsi que la longueur
de la plus grande monotonie a une esperance log2(n)+O(1).
Ceci est en accord une propriete' vue dans le cours de Steyaert:
Presque tous les mots contiennent tous les blocs (facteurs)
de taille (1-epsilon)*log2(n).
On a un problemem plus specifique mais des resultats plus precis.
Par exemple, un mot de longueur 100 contient avec une bonne
probabilite' une a ou b-monotonie de longueur 7.
Des statisticiens se sont amuses a verifier cette proprie'te'
contre-intuitive en isolant avec succes des suites reellement
aleatoires de suites pseudoaleatoires inventees par des humains.
Automates. Que faire face a des expressions ambigues? Un theoreme classique est a la base de la theorie des langages reguliers.
Exemple. Voir le poly pour la construction a la main d'un automate qui
reconnait un motif comme abb.
Complement de cours (pas fait). Donner le nombre moyen d'occurrences
d'un motif w de longueur k dans un mot aleatoire de
longueur n. Reponse: (2-2^{1-m})n en examinant
l'expression A*wA* qui est ambigue vis-a-vis des mots
contenant w,
mais "compte" exactement les occurrences.
 Qui suis-je?
Qui suis-je?
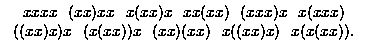
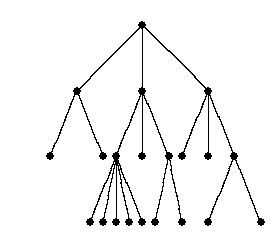
Definition. Soit D un ouvert simplement connexe du plan. Une fonction de C dans C est dite
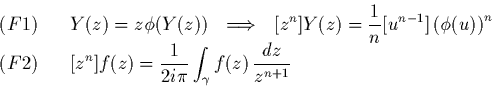
Cours 4 [13 Janvier 1999]

Exemples.
Partitions d'ensembles. De combien de facons partionner n objets en k classes non vides? Par exemple S[3,5]=25. Cela definit les nombres de Stirling de 2eme espece (ou "Stirling partition numbers"). (La notice biographique de Stirling, l'homme de sa formule, est ici.) On observe que le nombre de k-partitions est au nombre de k-surjections dans le rapport 1/k!, comme on aurait dit au XVIIIeme siecle. Donc, on sait faire.
Surjections et partitions ou k n'est plus fixe s'obtiennent en sommant les EGF correspondant a chaque cas k. On peut exploiter ces resultats en sommant et en developpant les coefficients. On obtient les nombres de Bell, sommes de nombres de Stirling, pour les partitions d'ensembles.
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
On a donc un nouveau dictionnaire et on en discute l'applicabilite'. On conclut par quelques exemples faits sous forme d'exercices commentes:
 Qui suis-je?
Qui suis-je?
Exercice. Justifier les assertions du fragment de texte suivant (ref: Frank Ruskey):
The number of derangements of length n, d(n) can be computed using the following well-known recurrence relation, n > 2:
The recurrence relation above can be manipulated so that it takes on the form
The d(n) numbers are sometimes called the subfactorial or rencontres numbers. The values of d(n) for n=0,1,2,...,10 are 1, 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, 1334961. This is sequence A000166(M1937) in Sloane's database of integer sequences.
le nombre d'arbres [enracines, non planaires, etiquetes] vaut n^(n-1).

Cours 5 [20 Janvier 1999]
Cours 6 [3 Fevrier 1999]
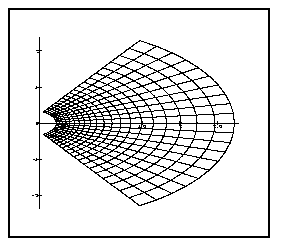
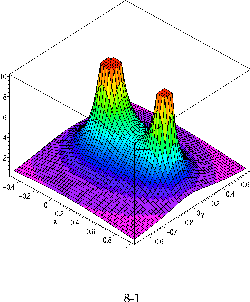
On commence alors a voir pourquoi on parle de tout ca. On veut acceder aux coefficients de series generatrices (de denombrement, mais peu importe!). Le theoreme des residus implique quais immedaitement que
Philosophiquement, ces deux theoremes dus a Cauchy sont fondamentaux. Il ramenent une caracteristqiue globale d'un objet analytique (son integrale sur un contour) a une caracteristique locale (le residu en un point). On peut aller pecher ailleurs les infos! L'\exemple du calcul de int(1/(1+z^2),z=-infty..+infty) illustre ce propos: on a juste besoin de developper un coup en z=+i. Exercice: calculer l'integrale avec z^8 qui remplace z^2. Meme Maple sait faire... et il le fait comme cela.
On continue et on montre deux choses:
Sur cette base, on part donc a la chasse aux singularites et on on trouve en exercice l'ordre exponentiel des coefficients lies aux denombrements suivants:
On se prepare a la fois suivante: presque toutes les fonctions obtenues par les methodes symboliques ont des singularites qui s'analysent et on peut effectivement en trouver l'asymptotique des coefficients. On annonce les deux theoremes principaux qui viendront, apres avoir defini la fonction Gamma:
Email: Philippe dot Flajolet AT inria dot fr