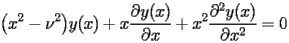\bigl(x^{2} - \nu^{2}\bigr) y (x) + x \frac{\partial y (x)}{\partial x} + x^{2} \frac{\partial^{2} y (x)}{\partial x^{2}} = 0

(x^2-nu^2)*y(x)+x*diff(y(x),x)+x^2*diff(diff(y(x),x),x) = 0

<math xmlns='http://www.w3.org/1998/Math/MathML'><semantics><mrow xref='id32'><mrow xref='id30'><mrow xref='id11'><mfenced><mrow xref='id7'><mrow xref='id3'><msup><mi xref='id1'>x</mi><mn xref='id2'>2</mn></msup></mrow><mo>-</mo><mrow xref='id6'><msup><mi xref='id4'>&nu;</mi><mn xref='id5'>2</mn></msup></mrow></mrow></mfenced><mo>&InvisibleTimes;</mo><mrow xref='id10'><mi xref='id8'>y</mi><mo>&ApplyFunction;</mo><mfenced><mi xref='id9'>x</mi></mfenced></mrow></mrow><mo>+</mo><mrow xref='id18'><mi xref='id12'>x</mi><mo>&InvisibleTimes;</mo><mfenced><mrow xref='id17'><mfrac><mo>&DifferentialD;</mo><mrow><mo>&DifferentialD;</mo><mi xref='id13'>x</mi></mrow></mfrac><mrow xref='id16'><mi xref='id14'>y</mi><mo>&ApplyFunction;</mo><mfenced><mi xref='id15'>x</mi></mfenced></mrow></mrow></mfenced></mrow><mo>+</mo><mrow xref='id29'><mrow xref='id21'><msup><mi xref='id19'>x</mi><mn xref='id20'>2</mn></msup></mrow><mo>&InvisibleTimes;</mo><mfenced><mrow xref='id28'><mfrac><mo>&DifferentialD;</mo><mrow><mo>&DifferentialD;</mo><mi xref='id22'>x</mi></mrow></mfrac><mrow xref='id27'><mfrac><mo>&DifferentialD;</mo><mrow><mo>&DifferentialD;</mo><mi xref='id23'>x</mi></mrow></mfrac><mrow xref='id26'><mi xref='id24'>y</mi><mo>&ApplyFunction;</mo><mfenced><mi xref='id25'>x</mi></mfenced></mrow></mrow></mrow></mfenced></mrow></mrow><mo>=</mo><mn xref='id31'>0</mn></mrow><annotation-xml encoding='MathML-Content'><apply id='id32'><eq/><apply id='id30'><plus/><apply id='id11'><times/><apply id='id7'><minus/><apply id='id3'><power/><ci id='id1'>x</ci><cn id='id2' type='integer'>2</cn></apply><apply id='id6'><power/><ci id='id4'>nu</ci><cn id='id5' type='integer'>2</cn></apply></apply><apply id='id10'><ci id='id8'>y</ci><ci id='id9'>x</ci></apply></apply><apply id='id18'><times/><ci id='id12'>x</ci><apply id='id17'><diff/><bvar><ci id='id13'>x</ci></bvar><apply id='id16'><ci id='id14'>y</ci><ci id='id15'>x</ci></apply></apply></apply><apply id='id29'><times/><apply id='id21'><power/><ci id='id19'>x</ci><cn id='id20' type='integer'>2</cn></apply><apply id='id28'><diff/><bvar><ci id='id22'>x</ci></bvar><apply id='id27'><diff/><bvar><ci id='id23'>x</ci></bvar><apply id='id26'><ci id='id24'>y</ci><ci id='id25'>x</ci></apply></apply></apply></apply></apply><cn id='id31' type='integer'>0</cn></apply></annotation-xml><annotation encoding='Maple'>(x^2-nu^2)*y(x)+x*diff(y(x),x)+x^2*diff(diff(y(x),x),x) = 0</annotation></semantics></math>