Loop-Erased Random Walks
Richard Kenyon
Université de Paris-Sud
Algorithms Seminar
May 31, 1999
[summary by Cyril Banderier]
A properly typeset version of this document is available in
postscript and in
pdf.
If some fonts do not look right on your screen, this might be
fixed by configuring your browser (see the documentation here).
Abstract
The loop-erased random walk is
the simple curve obtained by removing
in the chronological order the loops of the original random walk.
A basic aspect of these walks in Z2 is studied:
its average length (thus solving a conjecture of Guttmann).
The techniques are combinatorial and use a
bijection due to Temperley between maximal trees and perfect
coupling.
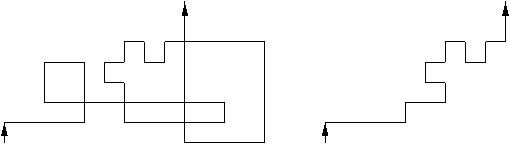
Figure 1: A random walk and its associated LERW
1 LERW=ST=DT
This is not a new equality between new complexity classes
but it simply emphasizes the fact that loop-erased random walk (LERW),
spanning tree (ST) and domino tiling (DT) are essentially the same object.
Indeed, in [12]
shows that, for a uniformly chosen spanning tree on a region of
Z2, the unique arc (branch) between two points has the same
distribution as the LERW between these two points.
Moreover, Temperley [13] gives a constructive
one-to-one correspondence
between spanning trees and domino tilings.
From the other talk of Richard Kenyon, we know that
domino tiling (the so-called two dimensional lattice dimer model,
a model which has some ties with Ising model)
is the only nontypical ad hoc statistical physical model
where conformal invariance
is proved, so representations of the Virasoro algebra [15]
could help finding critical exponents.
In order to solve this ``self-avoiding walk model''
(i.e., to set the critical exponent),
R. Kenyon does not use representation theory,
but a ``discrete Laplacian'', from which he
gets the full asymptotics. Whereas a lot is known about properties
of the continuous Laplacian [5], works on the discrete
Laplacian are more recent [10].
As conjectured by Bursill and Guttmann [4],
the exponent for LERW is 5/4. Richard Kenyon proves this
by applying the ``equality'' LEWR=ST on the following theorem
Theorem 1
On the uniform spanning tree process on N×Z, the expected
number of vertices on the arc from (0,0) to ¥ which lie
within distance N of the origin is N5/4+o(1).
The next theorem is sometimes attributed to Kirschoff [11] and
proven in [1].
Theorem 2 [Matrix-tree Theorem]
For a graph G with set of vertices {vi},
let
| D:= |
æ
ç
ç
ç
ç
è |
| deg(v1) |
0 |
0 |
|
0 |
·
·
· |
0 |
| 0 |
0 |
deg(vn) |
|
ö
÷
÷
÷
÷
ø |
|
-Adj(G), |
| |
| Õ |
| (j,k)¹ 0 |
| j=0,..., m-1 |
| k=0,..., n-1 |
|
|
|
æ
ç
ç
è |
4-2cos( |
|
)-2cos( |
|
) |
ö
÷
÷
ø |
. |
It is possible to extend this kind of result to a class of polygons
which are decomposable in rectangles, the so-called Temperleyan
polyominoes. (Triangulations are also a way, as there is a
determinant-like expression for triangles.)
Figure 2: A graph and its associated Temperleyan polyomino
The number of spanning trees of the graph is the number of domino tilings
of its Temperleyan polyomino.
Taking the log in the previous formula gives a special case
of the following theorem:
Theorem 3
Let UÌ R2 be a rectilinear polygon with V vertices. For each
e>0, let Pe be a Temperleyan polyomino in eZ2 approximating U in the natural sense (the corners of
pe are converging to the corners of U). Let Ae
be the area and Perime be the perimeter of Pe.
Then the log of the number of domino tilings of Pe is
where c0=G/p, G=1-1/32+1/52-··· is
Catalan's constant, c1=G/2p+log((2)1/2 -1)/4.
According to the author, ``Part of the motivation for the above
theorem is to validate a certain
heuristic, which attempts
to explain how the presence of the boundary affects the long-range
structure of a random tiling. In particular it attempts to explain
how the boundary affects the densities of local configurations far
from the boundary [3]. This heuristic is called the `phason strain'
principle.
The heuristic is as follows: The boundary causes the average
height function of a tiling to deviate slightly from its
entropy-maximizing value of 0. At a point in the region
where the average height function has nonzero slope, the ``local''
entropy there is smaller than the maximal possible entropy, by an
amount proportional to the square of the gradient of the average
height function.
The system behaves in such a way as to maximise the total entropy
subject to the given boundary values of the height function, and the
resulting average height function is the function which minimises the
(integral of) the square gradient. That is, the average height function
is harmonic.''
Anyway an exact application of the phason strain principle gives in
fact slightly different asymptotics (from the one given in the theorem 3), so
this principle is not totally valid
here, but however it gives a good approximation.
2 Height Function
For a given tiling, the height function h
is easily defined [14] by bicolouring the Temperleyan polyomino
(there are no adjacent vertices of the same colour):
Figure 3: A Temperleyan polyomino and the bicoloured associated graph
then, for each oriented edge AB on the border of a domino,
| h(A)-h(B):=
|
ì
í
î |
| +1 |
if the square on the left of AB is black, |
| -1 |
otherwise. |
|
|
Note that, up to an arbitrary additive constant, the height of the
boundary is independent of the tiling.
For a smaller and smaller lattice (e.g., e Z2), one can
approximate any domain U of C.
For a very fine lattice (in fact, taking the limit when
e® 0), one can study the probability of appearance in
the tiling of some patterns, their repartition in the tiling and
also how the shape of the boundary influences the tiling.
It appears that there are links with conformal theory, as
explained below.
Let Pe be a Temperleyan polyomino associated
to a rectilinear polygon U of C.
Now, let he be the average height function of Pe,
that is the average height over all domino tilings of Pe
and then define
For xÎ ¶ U, h(x) is defined by continuity from values of
h in the interior.
The remarkable fact is that this limiting average height function h
can be expressed as
| h(v)= |
|
Á |
ó
õ |
|
|
|
æ
ç
ç
è |
F+(v,z)- |
|
ö
÷
÷
ø |
du=- |
|
Á log Ã'(z), |
References
- [1]
-
Brooks (R. L.), Smith (C. A. B.), Stone (A. H.), and Tutte (W. T.). --
The dissection of rectangles into squares. Duke Mathematical
Journal, vol. 7, 1940, pp. 312--340.
- [2]
-
Burton (Robert) and Pemantle (Robin). --
Local characteristics, entropy and limit theorems for spanning trees
and domino tilings via transfer-impedances. The Annals of Probability,
vol. 21, n°3, 1993, pp. 1329--1371.
- [3]
-
Destainville (N.), Mosseri (R.), and Bailly (F.). --
Configurational entropy of codimension-one tilings and directed
membranes. Journal of Statistical Physics, vol. 87, n°3-4,
1997, pp. 697--754.
- [4]
-
Guttmann (A.) and Bursill (R.). --
Critical exponent for the loop-erased self-avoiding walk by
Monte-Carlo methods. Journal of Statistical Physics, vol. 59,
1990, pp. 1--9.
- [5]
-
Kac (Mark). --
Can one hear the shape of a drum? American Mathematical
Monthly, vol. 73, n°4, part II, 1966, pp. 1--23.
- [6]
-
Kenyon (Richard). --
Rigidity of planar tilings. Inventiones Mathematicae, vol. 107,
n°3, 1992, pp. 637--651.
- [7]
-
Kenyon (Richard). --
Tiling a polygon with parallelograms. Algorithmica, vol. 9,
n°4, 1993, pp. 382--397.
- [8]
-
Kenyon (Richard). --
Local statistics of lattice dimers. Annales de l'Institut Henri
Poincaré. Probabilités et Statistiques, vol. 33, n°5,
1997, pp. 591--618.
- [9]
-
Kenyon (Richard). --
Tilings of convex polygons. Annales de l'Institut Fourier,
vol. 47, n°3, 1997, pp. 929--944.
- [10]
-
Kenyon (Richard). --
Tilings and discrete Dirichlet problems. Israel Journal of
Mathematics, vol. 105, 1998, pp. 61--84.
- [11]
-
Kirchhoff (G.). --
Über die Auflösung der Gleichungen, auf welche man bei der
Untersuchung der linearen Verteilung galvanischer Ströme geführt
wird. Annalen für der Physik und der Chemie, vol. 72,
1847, pp. 497--508.
- [12]
-
Pemantle (Robin). --
Choosing a spanning tree for the integer lattice uniformly. The
Annals of Probability, vol. 19, n°4, 1991,
pp. 1559--1574.
- [13]
-
Temperley (H. N. V.). --
Enumeration of graphs on a large periodic lattice. In Combinatorics. London Mathematical Society Lecture Note Series,
pp. 155--159. --
Cambridge University Press, 1974. Proceedings of the
British Combinatorial Conference, University College, Wales, Aberystwyth,
1973.
- [14]
-
Thurston (William P.). --
Conway's tiling groups. The American Mathematical Monthly,
vol. 97, n°8, 1990, pp. 757--773.
- [15]
-
Virasoro (M. A.). --
Physical Review D. (3), 1970, pp. 2933--2936.
- 1
- Like other recent preprints of the author, they
are available at his home page
http://topo.math.u-psud.fr/~kenyon/
This document was translated from LATEX by
HEVEA.