Fraïssé-Ehrenfeucht Games and Asymptotics

Alan Woods

University of Western Australia

Algorithms Seminar

March 23, 1998

[summary by Julien Clément and Jean-Marie Le Bars]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract
Fraïssé-Ehrenfeucht games are played on two structures, where a structure might, for example, consist of a unary function mapping a finite set into itself. Via generating series and a Tauberian theorem, it is possible to investigate the asymptotic probability of having a winning strategy for such a game, when it is played using a fixed structure, and a random structure of size n, with n going to infinity. Actually for unary functions this gives a convergence law for all properties of the structure which are definable in monadic second order logic.

1   Introduction

We consider here structures A based upon a set A and finitely many relations Ej of finite arity
A= < A,E1(x,y),E2(x),E3(x,y,z), ... > .
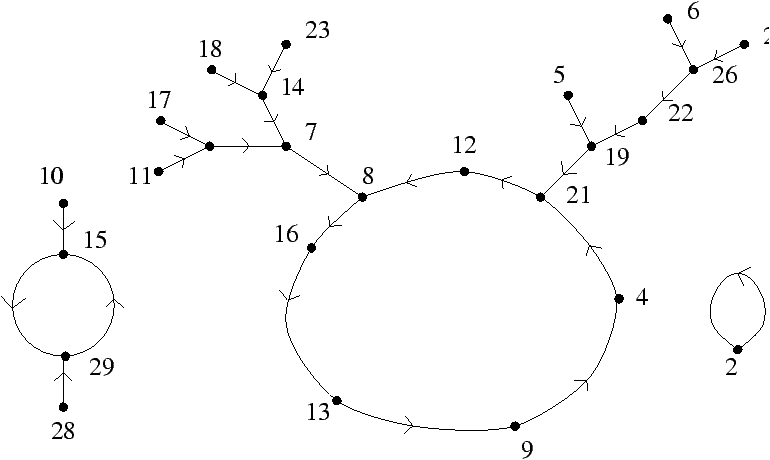
A classical example is a set of vertices V and an edge relation E(x,y) so that V=<V,E> describes a graph. We can also think of simple structures A=<A,f> consisting of a finite set A and a unary function mapping this set into itself (see fig. 1). This unary function induces a binary relation F(x,y) Û f(x)=y.

Figure 1: Graphical representation a structure A=<[29],f> (where the unary function f maps {1,2,..., 29} on itself).


In order to use generating functions (see the last section) we need to translate a decomposition property of structures to the generating functions: this will be done through the disjoint union. Let us consider two structures
A= A,E
A
 
1
, ... and B= B,E
B
 
1
, ... .
If A Ç B=Ø and each Ei A has the same arity as Ei B, the disjoint union is defined as the structure whose domain is the union of the domains and whose relations are the unions of the corresponding relations
A ú`½ B= A È B, E
A
 
1
È E
B
 
1
,... .
A class of structures has components if each structure can be uniquely decomposed into disjoint unions of structures (called component structures) from some components classes. For structures A=<[n],f>, where [n] denotes {1,...,n} and f is a unary function, one can define component classes relative to the size of the unique loop present in each connected component of the graph of f. From this point of view, for the structure A of figure 1, we see three components. The first component of A consists of two component structures in the first component class (the class corresponding to loops of size one i.e. fixed elements of f). The two other components consist in two single component structures and are respectively in the component classes 2 and 7 (relatively to the size of the loop).
Let us define the rank r(j) of a formula j in the context of the second order logic (or MSO logic for short) inductively by:
  1. If j has no quantifiers, then r(j)=0;
  2. If j is ¬ s, then r(j)=r(s);
  3. If j is obtained from s1, s2 by the application of a binary propositional connective (e.g., if j is s1 Ù s2, s1 « s2, etc.) then r(j)=max{r(s1),r(s2)};
  4. If j is of the form " v s, $ v s, " V s or $ V s for some variable v, V, then r(j)=r(s)+1.
A sentence is a formula that has no free variables and is a property of a structure.
The key observation is that there are only finitely many inequivalent sentences x1, ..., xm of rank r. Hence every structure A satisfies exactly one of the sentences (also of rank r)
y1=x1 Ù ... Ù xm, y2=¬ x1 Ù ... Ù xm,..., y
 
2m
=¬ x1 Ù ... Ù ¬ xm.
Given a rank r (and implicitly the sentences y1,...,y2m), for each i Î {1,...,2m} we define the class of structures which satisfies yi. These classes can be viewed as equivalence classes of Fraïssé-Ehrenfeucht games.

2   Fraïssé-Ehrenfeucht Games

The goal is to see whether or not we can distinguish two structures in a r moves game. The game is played with two structures A=<A,E1 A, ...> and B=<B,E1 B, ...>. Dupe wins if after r moves the map {ai,...} ® {bi,...} taking ai |® bi is an isomorphism of the induced substructures of < A,Aj,...>, < B,Bj,...> on these sets. We write
A ºr B Û Dupe has a winning strategy.
Note that there is no ex æquo (either Spoil or Dupe has a winning strategy). These games are the main tools for proving the following theorems:
Theorem 1   Let us consider some structures A1, A2, B1, B2, one has
A1 ºr B1, A2 ºr B2 Þ A1 ú`½ A2 ºr B1 ú`½ B2.
Theorem 2   For every structures A and B, one has
A ºr B iff there exists i such that A |= yi and B |= yi,
where the sentences yi's are defined in the first section.
Corollary 1   There are only finitely many ºr classes.
Another problem consists in determining the ºr class of a given structure A. It is solved if we know the number of component structures lying in each ºr component class (or color if we think of ºr as a colouring). On figure 2, we have 5 component classes C1,..., C5 relative to the º3 relation (namely triangles, squares, cycles of odd length strictly greater than 3, cycles of even length strictly greater than 4). The numbers of component structures in each component of the structure A are respectively m1=5,m2=1,m3=0,m4=4.

Figure 2: The components classes C1,..., C4 relative to º3 (left), the structure A and its four components (right).

3   Counting Structures with Components

We count either
  1. the number an of labelled structures with n elements, or
  2. the number bn of unlabelled structures with n elements (which is, also, the number of nonisomorphic structures with n elements).
Here we focus on counting labelled structures. So the exponential generating series
a(x)=
¥
å
n=0
an
n!
xn
will prove highly useful. Indeed, for a structure A= G ú`½ H, letting a(x), h(x) and g(x) be the corresponding exponential generating series, we write
a(x)=g(x) h(x)    or   a(x)=
g(x)2
2
,
whether G and H are in different classes or not. By induction the exponential generating series associated to A= G(1) ú`½ ... ú`½ G(m) the disjoint union of m structures G(1),..., G(m), is
a(x)=g(1)(x) ··· g(m)(x)   or    (x)=
g(x)m
m!
,
respectively if G(1),..., G(m) are all from different classes or all in the same class. Hence the generating series a(x) for structures with components in the component class C is
a(x)=1+c(x)+
c(x)2
2!
+ ...+
c(x)m
m!
+···=ec(x),
where c(x)=ån cn/n!xn (cn is the number of labelled structures in the component class C with n elements).
There is a connection with monadic second order logic due to Compton [2]. Let us consider the component classes (relatively to ºr) C1, ..., Ck (so that the generating series for whole component class is c(x)=åi=1k ci(x)). There is a unique k-tuple (m1,...,mk) associated to each structure A, where mi is the number of component structures of A lying in the i-th component class Ci. Moreover for two structures A and B (with k-tuples (m1,...,mk) and (n1,...,nk)), there is an integer R=R(r) such that if " i Î {1,...,k} either mi=ni or mi,ni ³ R, then A ºr B (plainly speaking, too many component structures of the same component class prevent to distinguish structures). Hence for a sentence j of rank r, the number of labelled structures A such that A |= j depends only on m1,...,mk where mi Î {0,1,...,R-1,¥} is the number of components in Ci (¥ means anything equal to at least R=R(r)). Considering the exponential generating series aj(x)=åanj/n! where anj the number of labelled structures with n elements satisfying j, we can write
a
 
j
(x)=
 
å
(m1,...,mk) Î S
c1(x)
m1
 
m1!
···
ck(x)
mk
 
mk!
,
where S is finite and ci(x)¥/¥! denotes åm=R¥ci(x)m/m!= eci(x)-åm=0R-1 ci(x)m/m!. The series aj(x) is a finite sum of very similar terms. It is enough just to consider a series of the form
a
 
j
(x)=
c1(x)
m1
 
m1!
···
ct(x)
mt
 
mt!
e
ct+1(x)
 
··· e
ck(x)
 
.
This formula means that a structure A satisfying j has exactly mi components in the class i for i Î {1,...,t} and any number of components in the other classes. We want to know anj or equivalently µn(j)=anj/an, the fraction of structures of size n satisfying j. We are also interested in the asymptotic probability µj=limn ® ¥ µn(j), when this limit exists.
It is Compton's idea to use partial converses Tauberian lemmas to get limit laws for µn. Here is a sample theorem whose proof is based on such lemmas.
Theorem 3   For any class with components, if an/n! ~ C tn/na and cn/n!=O(tn/n) (with a> -1) then µ(j)=limn® ¥ µn(j) exists for all MSO sentences j and is equal to aj(r)/a(r).
Due to known results about an and cn for structures with one unary function, we have also
Corollary 2   The asymptotic probability µj always exists with one unary function.

References

[1]
Compton (Kevin J.). -- Application of a Tauberian theorem to finite model theory. Archiv für Mathematische Logik und Grundlagenforschung, vol. 25, n°1-2, 1985, pp. 91--98.

[2]
Compton (Kevin J.). -- A logical approach to asymptotic combinatorics. II. Monadic second-order properties. Journal of Combinatorial Theory. Series A, vol. 50, n°1, 1989, pp. 110--131.

[3]
Fagin (Ronald). -- Probabilities on finite models. Journal of Symbolic Logic, vol. 41, n°1, 1976, pp. 50--58.

[4]
Glebskii (Ju. V.), Kogan (D. I.), Liogon'kii (M. I.), and Talanov (V. A.). -- Volume and fraction of satisfiability of formulas of the lower predicate calculus. Kibernetika (Kiev), vol. 5, n°2, 1969, pp. 17--27. -- English translation Cybernetics, vol. 5 (1972), pp. 142--154.

[5]
Woods (Alan). -- Counting finite models. The Journal of Symbolic Logic, vol. 62, n°3, September 1997, pp. 925--949.
This document was translated from LATEX by HEVEA.