Colouring Rules for Finite Trees and Probabilities of Monadic Second Order Sentences

Colouring Rules for Finite Trees
and Probabilities of Monadic Second Order Sentences

Alan R. Woods

University of Western Australia

Algorithms Seminar

March 10, 1998

[summary by Cyril Chabaud]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract

Given a set of colouring rules applying to the vertices of any finite rooted tree, we study the asymptotic behaviour of the probability that an n vertex tree has a given root colour. These results will prove that the fraction of labelled or unlabelled rooted trees satisfying any fixed monadic second-order sentence converge to limiting probabilities.

1 Introduction

Given a finite rooted tree and a set of k colours, the vertices are coloured from the leaves to the root according to a set of colouring rules, namely a function h:N^k ®{1,2,...,k}. The colour assigned to a vertex depends only on the number C₁,...,C_k of its immediate predecessors having colour 1,...,k.

Example 1 Let

h(C_black,C_white)=

ì
í
î

black	if C_black is even
white	if C_black is odd

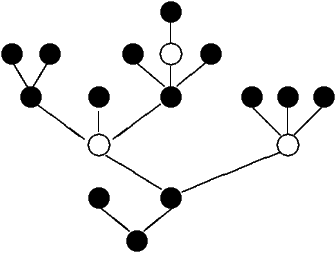be a set of colouring rules. From the definition of h, the leaves of the following tree are coloured black and we find its root colour is black.

Note that the root of a finite rooted tree is black iff the number of its vertices is odd, with the set of colouring rules defined above.

Let µ_n[i] be the fraction of n vertex labelled trees with root colour i.

Theorem 1 Let µ [i]=lim_n®¥ µ_n[i] and the corresponding Cesàro limit

[i]=

lim

n®¥

m=1

µ_m[i].

For any set of colouring rules h, µ^_[i] exists for all colours i=1,...,k and either

µ^_[i]>0 or
$ c>1 such that µ_n[i]<c^-n for all sufficiently large n.

Although the existence of µ [i] implies the existence of µ^_[i] in general, the converse needs additional conditions to be true.

2 Applications to Logic

2.1 First Order Logic

There exists an analogous result for first order sentences about a graph. The language in which these sentences are written contains the usual quantifiers, parentheses and connectives with an additional predicate symbol E(x,y) expressing the fact that vertex x and vertex y are joined by an edge.

Example 2 The following expression is a first order logic sentence expressing ``every vertex has degree 2'':

" x$ y₁$ y₂(¬ y₁=y₂Ù" z(E(x,z)Û z=y₁Ú z=y₂)).

Fagin [3], Glebskii, Kogan, Liogon'kii and Talanov [4] have proved the following result

Proposition 1 Let µ_n(j) be the fraction of n vertex graphs with property j. For every first order sentence j about a graph, µ(j)=lim_n®¥ µ_n(j) exists and µ(j)=0 or 1.

That the only possible values are 0,1 is a consequence of the fact that graphs have no roots.

2.2 Monadic Second Order Logic

The situation for monadic second order sentences about a rooted tree is quite different since the language provides a constant symbol R denoting the root, and it can handle sets of vertices using second order variables.

Determining the satisfiability of a monadic second order sentence j of rank r reduces to finding the root colour of a rooted tree T for a particular system of colouring rules. Results arising from Compton's method of components [2] establish that if j is a sentence of rank r, then there exists sentences y₁,...,y_k of rank r such that:

Every finite rooted tree satisfies exactly one y_i;
Every j of rank r is equivalent to Ú_{iÎ S}y_i for some set S.

If T is a rooted tree that has component trees T₁,..., T_m that satisfy sentences y_i_₁,...,y_i_{_m}, then there exists a unique i such that T satisfies y_i, and this particular i can be interpreted as the root colour of T. (For details see [8]).

2.3 Boolean Formulas

Assume we have M boolean variables x₁,...,x_M. Then the colours turn out to be the 2²^{^M} boolean functions Y_i. The existence of the limiting probability µ[i] is stated in the following theorem:

Theorem 2 Let µ_n[i] be the fraction of formulas of size n which compute the boolean function Y_i, iÎ{1,...,2²^{^M}}. Then lim_n®¥µ_n[i]=µ[i] exists and µ[i]>0.

3 Enumeration of Rooted Trees

3.1 Labelled Rooted Trees

We use generating functions methods to determine µ^_[i] in the labelled case. Note that a similar proof can be done for the unlabelled case.

Let T(x) denote the generating function for labelled rooted trees:

T(x)=t₁x+

t₂

x²+

t₃

x³+... +

t_n

xⁿ+···

where t_i is the number of i vertex labelled rooted trees. Since this structure is decomposable, we easily obtain a functional equation on T(x) and find:

T(x)=xe^T(x).

Hence, using Lagrange inversion we get:

T(x)=x+

x²+

3²

x³+... +

n^n-1

xⁿ+···.

The radius of convergence of this series is r=1/e, x=r is the only singularity on the circle of convergence, where there exists a constant h₁ such that T(x) behaves like 1+h₁(r-x)^1/2. One can then apply Darboux's theorem and find that t_n behaves asymptotically like t_n~ Cr^-nn^-3/2.

3.2 Labelled Trees with a Particular Root Colour

Let T_i(x) be the generating function for labelled trees with root colour i,

T_i(x)=x

M₁,...,M_k

h(M₁,...,M_k)=i

M₁

(x)

M₁!

···

M_k

(x)

M_k!

To find y_i=T_i(x) we have to solve the system:

{y_i=g_i(x,y₁,...,y_k)}

iÎ{1,...,k}

where

g_i(x,y₁,...,y_k)=x

M₁,...,M_k

h(M₁,...,M_k)=i

M₁

M₁!

···

M_k

M_k!

4 Cesàro Probabilities

To determine probability µ^_[i] we use a partial converse of the following Abelian theorem:

Theorem 3 Let b(x)=å_{n³ 0}b_nxⁿ, c(x)=å_{n³ 0}c_nxⁿ and r be the radius of convergence of b(x). If lim_n®¥c_n/b_n=µ and å_{n³ 0} b_nrⁿ diverges then:

lim

x®r-

c(x)/b(x)=µ.

Setting c(x)=T_i^'(x) and b(x)=T^'(x), we find that the conditions above are satisfied since lim_{x®r -}T^'(x)=¥. The result is given by the following Tauberian theorem:

Theorem 4 [Compton [1]] Let b_n~ Cn^a, a>-1, b_n¹ 0 for n³ 0, c_n=O(b_n). If

lim

x®r -

c(x)/b(x)=µ,

where r is the radius of convergence of b(x)=å_{n³ 0} b_nxⁿ then:

lim

n®¥

M=1

c_M

b_M

=µ.

Since

(x)=

¶ g_i

¶ x

(x,T_i(x),..., T_k(x))+

j=1

(x)

¶ g_i

¶ y_j

(x,T_i(x),...,T_k(x)),

when x®r -, we have

[i]=

i=1

¶ g_i

¶ y_j

[j] for i=1,...,k.

Thus, the µ^_[i] are linearly dependent, as the following matrix relation shows:

é
ê
ê
ê
ê
ê
ê
ê
ê
ê
ê
ë

[i]

·
·
·

[k]

ù
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
û

=W(r)

é
ê
ê
ê
ê
ê
ê
ê
ê
ê
ê
ë

[i]

·
·
·

[k]

ù
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
û

where W(r)=

é
ê
ê
ê
ê
ê
ê
ê
ê
ê
ê
ë

¶ g₁

¶ y₁

···

¶ g₁

¶ y_k

·
·
·

¶ g_k

¶ y₁

···

¶ g_k

¶ y_k

ù
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
û

yielding the linear system: (Id-W(r)) ^T[µ^_[i]···µ^_[k]]=0. Here W(r) is a stochastic matrix, and from the theory of nonnegative matrices, the rank of (Id-W(r)) is k-1. Consequently, the linear system above has a unique solution satisfying µ^_[i]+... + µ^_[k]=1.

We associate with W(r) its dependency digraph D. Namely, we put a directed edge from vertex j to vertex i iff ¶ g_i/¶ y_i(r,T₁(r),...,T_k(r ))>0. In other words, this directed edge exists iff $ C₁···$ C_k (C_j>0Ù h(C₁,...,C_k)=i)

Property 1 There is a unique strong component S in D with the property that, for every colour j, there is a directed edge in D from j to some colour in S. S is called the principal component of D.

This property is the key point to prove the first part of theorem 1:

Theorem 5 For any system of colouring rules, µ^_[i] exists for all colours i. Moreover, if S is the principal component of dependency digraph D then

[i]>0ÜÞ iÎ S.

Proof. From the property above there exist A(x) and B(x) such that

W(x)=

é
ë

A(x)	C(x)
	B(x)

ù
û

and A(x) is an irreducible matrix. Matrix A(x) is indexed by S={1,...,s} after renumbering. Since 1 is the largest eigenvalue of A(r), from Perron-Frobenius theory (see for instance [7]) there is a unique normalized solution m₁,...,m_s of

é
ê
ê
ê
ê
ë

m₁

·
·
·

m_s

ù
ú
ú
ú
ú
û

=A(r)

é
ê
ê
ê
ê
ë

m₁

·
·
·

m_s

ù
ú
ú
ú
ú
û

with m₁>0,...,m_s>0. Then we just show that 1 cannot be an eigenvalue of B(r) and prove that [m₁,...,m_s,0,...,0] is a normalized eigenvector of W (r).
The colours that do not belong to the principal component S have probabilities that converge exponentially to zero, as the following theorem shows:

Theorem 6 For any system of colouring rules, if iÏS then there is some c>1 such that µ_n[i]<c^-n. (The same property holds in the unlabeled case).

Proof.[Sketch of proof] We prove that for each i such that iÏS, T_i(x) has an analytic continuation on the circle of convergence of T(x), meaning that the radius of convergence of T_i(x), r_i, is greater than r. Since µ_n[i]=t_nⁱ/t_n, this leads to desired result. For details, see [8].

5 Existence of µ[i]

We examine here a sufficient condition to ensure the existence of µ[i] rather than just µ^_[i]. The existence of µ[i] is conditioned by the presence of a unique singularity on the circle of convergence of T_i(x), indeed:

Lemma 1 Let A(x) be the irreducible block of matrix W(x). If det(A(x)-I)¹ 0 for all x¹r on the circle |x|=r then µ[i] exists for all iÎ S. The probabilities µ[1],...,µ[s] are all strictly positive and form the unique normalized solution of

é
ê
ê
ê
ê
ë

µ[1]

·
·
·

µ[s]

ù
ú
ú
ú
ú
û

=A(r)

é
ê
ê
ê
ê
ë

µ[1]

·
·
·

µ[s]

ù
ú
ú
ú
ú
û

Proof. See [8]
If we look again the first example, clearly µ[1] and µ[2] do not exist since series T_black(x) and T_white(x) have two singularities on the circle |x|=r.

The next theorem is a sufficient criterion on colouring rules to guarantee the convergence of µ_n[i]:

Theorem 7 Suppose that for each iÎ{1,...,k} there exists at least one pair of rules of the following sort, namely: there exists C₁>1,...,C_k>1 such that h(C₁,...,C_i-1,...,C_k)=h(C₁,...,C_i,...,C_k). Then µ[i] exists and µ[i]>0 for all iÎ S.

Proof.[Sketch of proof] We prove that det(I-W(x))¹ 0 for all |x|£r except x=r, and that each T_i(x) has at most x=r as a singularity on the circle |x|=r.

6 Open Problems and Extensions

Characterize the asymptotic behaviour of µ_n[i] for general systems of colouring rules;
Assume j is a monadic second order sentence. For labeled free trees, McColm [6] proved probability µ_n(j) satisfied a 0-1 law;
What happens when we distinguish multiple roots?
Take unary functions y=f(x). If for some e>0 and g>0, probability µ_n(j)>e/n^g for infinitely many n, is there always a simple asymptotic formula for µ_n(j)?

A partial answer to this last question is that µ_n(j) converges, and it has been given in the labeled case for g=0 by Compton and Shelah; Woods (also in the unlabeled case) [9]; Luczak and Thoma [5].

References

[1]: Compton (Kevin J.). -- Application of a Tauberian theorem to finite model theory. Archiv für Mathematische Logik und Grundlagenforschung, vol. 25, n°1-2, 1985, pp. 91--98.
[2]: Compton (Kevin J.). -- A logical approach to asymptotic combinatorics. II. Monadic second-order properties. Journal of Combinatorial Theory. Series A, vol. 50, n°1, 1989, pp. 110--131.
[3]: Fagin (Ronald). -- Probabilities on finite models. Journal of Symbolic Logic, vol. 41, n°1, 1976, pp. 50--58.
[4]: Glebskii (Y. V.), Kogan (D. I.), Liogon'kii (M. I.), and Talanov (V. A.). -- Range of degree and realizability of formulas in the restricted predicate calculus. Kibernetika (Kiev), vol. 5, n°2, 1969, pp. 17--28. -- [Engl. Transl. Cybernetics, vol. 5, 142--154 (1972)].
[5]: Luczak (Tomasz) and Thoma (Lubos). -- Convergence of probabilities for the second order monadic properties of a random mapping. Random Structures & Algorithms, vol. 11, n°3, 1997, pp. 277--295.
[6]: McColm (Gregory L.). -- MSO asymptotics on random free trees (and random strings). -- 1996. Preprint.
[7]: Minc (Henryk). -- Nonnegative matrices. -- John Wiley & Sons Inc., New York, 1988, Wiley-Interscience Series in Discrete Mathematics and Optimization, xiv+206p. A Wiley-Interscience Publication.
[8]: Woods (Alan R.). -- Coloring rules for finite trees, and probabilities of monadic second order sentences. Random Structures & Algorithms, vol. 10, n°4, 1997, pp. 453--485.
[9]: Woods (Alan R.). -- Counting finite models. The Journal of Symbolic Logic, vol. 62, n°3, 1997, pp. 925--949.

This document was translated from L^AT_EX by H^EV^EA.