ECPP Comes Back

François Morain

LIX, École Polytechnique

Algorithms Seminar

April 20, 1997

[summary by Guillaume Hanrot]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

1   Introduction

Prime numbers have always attracted attention from both mathematicians and computer scientists. One of the reasons is perhaps the fact that the definition of a prime is very simple, most of the famous conjectures concerning primes can be stated in elementary terms, yet these problems are extremely high and the techniques involved are most often very sophisticated.

We outline a few more concrete motivations to study prime numbers and to try to discover huge prime numbers (that is, apart from trying to understand the asymptotic properties of primes via experimentation): The main trends in the computational study of primality are the following: In this talk we will describe the solutions to the first problem, the so-called ``primality testing'' problem, but we shall call it ``primality proving'', to emphasize the fact that we shall describe an algorithm with produces an easy-to-check proof together with its yes/no answer.

We shall first make a quick overview of existing primality tests; we will then concentrate on the ECPP test, describing its principles, its main features and recent progresses in theory and implementation. We shall end by a list of current records and perspectives.

2   Primality Tests: an Overview

A general reference for all the tests mentioned in this section is [9].

2.1   Compositeness Tests

This section covers the so-called ``compositeness tests''. Given a number N, these tests check whether N verifies a certain criterion, which is known to be the case if N is prime. If it is not so, the number is known to be composite, whence the name of this group of tests. However, if the test is passed, one can by no means be sure that N is prime.

In a nutshell, they are fast (O((log N)3)), but can only provide one with negative answers to the question ``is N prime''. Examples of such tests include: Due to their efficiency, and their relative accuracy concerning ``small'' numbers N when suitably combined, those tests are usually implemented under the name isprime in various computer algebra packages (Maple, Pari, ...).

2.2   Primality Proving

A real primality proof is somewhat different from the tests described in the last section. It should be able to give an answer, either yes or no, together with a proof, for any given number N. Of course, it should at the same time be as fast as possible.

Examples of such tests include:

3   The Principles of ECPP

In this section, we shall describe the principles on which rests ECPP (which, by the way, stands for Elliptic Curves Primality Proving). This test is an analog of the N-1 test which has been known for long, and is very efficient when the number N-1 is smooth, i.e., has only small prime factors.

3.1   The N-1 Test

Assume that N is neither even nor a prime power (these two possibilities can be easily avoided). Then we have the following

Theorem 1   N is prime iff (Z/NZ)* is a cyclic group. In other words, there exists aÎZ such that aN-1 º 1 mod N, and for all prime p dividing N-1, a(N-1)/p ¬ º1 mod N.

The triple (N, {p | (N-1) }, a) is a certificate of primality for N. It is very easy to check from these data that N is indeed prime.

A more practical version of this theorem (due to Pocklington, 1914) allows one to restrict to a set of prime factors of (N-1) whose product is larger that (N)1/2. This however does not address the main problem of the method, which is the need to factor N-1, at least to some extent. Compared to this, finding a is a merely trivial matter: if the generalized Riemann hypothesis is true, there exists one such a smaller than 2(log N)2.

3.2   Elliptic Curves

The main idea in the N-1 test is that if a certain group is cyclic, then N is prime. Thus we just need to find a generator. Proving that a given number is a generator amounts mostly, from a computational point of view, to factor to some extent the order of the group.

The idea of Goldwasser and Kilian was to construct a vast number of groups of different orders with the same property that the N-1 test, so that one can hope to find at least one such group with a smooth order.

Let us introduce quickly elliptic curves. Let K be a field of characteristic ¹ 2,3. An elliptic curve defined over K is a projective nonsingular curve defined by an equation Y2Z = X3 + a XZ2 + bZ3, where (a,b)Î K×K. More concretely, E(K)={(X,Y,1), Y2=X3+aX+b} È {(0,1,0)}, this last point being ``at infinity''. The non-singularity can be expressed by the condition D := 4a3+27b2 ¹ 0. To an elliptic curve, we can attach an invariant defined by j(E)=1728 (4a3/D). Conversely, given j0Î K, the family of elliptic curves Y2 = X3 + 3j0/(1728 - j0) c2X + 2j0/(1728-j0)c3 has j-invariant j0 (except when j0=0 or 1728; for j0=1728, take Y2 = X3+aX, for j0=0, take Y2=X3+b). 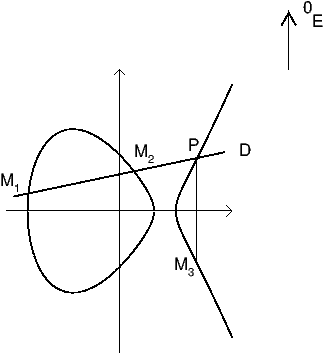The set of points of an elliptic curve over a certain field can be given a group structure by using the following rules: the neutral element 0E is the point at infinity; if A, B, C lie on the same line, then A+B+C=0E. (Note that if a line has at least two points of intersection with a cubic (counting multiplicities) over a given field, then it has three, so that the addition is well-defined over the ground field.) This rule is illustrated on the following picture: M1+M2+P=0E and 0E+P+M3=0E, so that M1+M2=M3.


If K = Fp is a prime finite field, the group E(K) is finite. We can however be much more precise:

Theorem 2  [Hasse, 1933; Deuring, Waterhouse]  
  1. One has |# (E(Fp)) - (p+1)| £ 2(p)1/2,
  2. for all t integer in ]-2(p)1/2, 2(p)1/2[, there is a curve E defined over Fp with exactly p+1-t points over Fp.

We now have to (a) find a primality criterion linked with these groups (b) make the second part of this theorem effective. The main feature of ECPP is the use of complex multiplication to solve problem (b).

3.3   A Primality Criterion

Both Goldwasser and Kilian's method and the ECPP test are based on the following
Theorem 3   Let B be an integer, m and s two integers such that s|m, E an elliptic curve defined over Z/NZ and P a point on E. Then mP=OE and
" q prime| s, [m/q] P = (X : Y : Z), gcd(Z,N)=1Þ " p|N, #E(Z/pZ) º 0mod s.

If we can find a point P satisfying the conditions of left part of this implication with s > (([)1/24]N+1)2, then using Hasse's theorem we see that any prime p dividing N is larger than (N)1/2, which means that N is prime. The primality can be easily checked given (E,m,s, {q|s}, P) (the certificate).

This theorem, together with Schoof's algorithm which enables one to compute the number of points of an elliptic curve on a finite field in time O((log N)8), leads to the following algorithm (Goldwasser and Kilian, [10]):

Repeat Choose a random elliptic curve E modulo N, compute #E(Z/NZ).
until the primality criterion can be applied [ i.e., #E(Z/NZ) is smooth ]


Note that the application of the criterion is most often recursive: one factors #E(Z/NZ), and gets one large factor presumably prime. ECPP is then recursively used to actually prove the primality of this large factor. Since this factor is at worst N/2 + o(N), the recursion depth is O(log(N)). The complexity is thus O((log N) (log N)8), under the heuristic assumption (verified in practice) that there are many good curves (giving smooth #E(Z/NZ)).

This algorithm has been generalized to the case of curves of genus 2 (i.e., curves Y2 = f(X), where deg(f)=5 or 6) by Adleman and Huang. In that context, the algorithm can be proved to be polynomial probabilistic.

However, both of these algorithms are definitely unpractical. First, Schoof algorithm has never been very efficient, and even with the more recent improvements which reduce the complexity to O((log N)6), 4000 hours are needed to compute the cardinality of a single curve linked with the primality of a 500-digits number.

3.4   Complex Multiplication, or Finding Curves with a Smooth Number of Points

A partial answer to the question (b) raised above is given by the theory of complex multiplication.

Let p be a prime number such that 4p is of the form U2+DV2, where (U,V,D) are integers, with D>0. Class field theory of imaginary quadratic fields tells us that given D, one can construct a polynomial HD(X), of degree h(-D) (the class number of Q((-D)1/2)), the roots of which generate the maximal abelian unramified extension (class field) of Q((-D)1/2). Moreover, this polynomial splits on Fp as a product of linear factors, and its roots are the j-invariants of elliptic curves E with #E(Fp) = p+1-U.

For instance, for D=4, HD(X) = X-1728 and one can take for E the curve of equation Y2 = X3+aX. If p º 1 mod 4 or p=2, 4p = U2+V2 and #E = p+1-U. Note that U is only defined up to sign, and according to the choice of a (square or non-square mod p), both possibilities can occur.

The previous algorithm becomes:

repeat
    repeat
       Find D such that 4N = U2 + DV2, and compute (U,V) using Cornacchia's algorithm.
    until N+1-U is smooth;
    find a root of HD(X) mod N (use Berlekamp's algorithm); construct E so that j(E)=j0,
    and choose among the family constructed an E such that #E = N+1-U,
until one of the primality theorems can be applied.

4   Recent History

4.1   Recent Improvements

In this section we describe shortly the recent improvements included in the last version of the ECPP software.

First of all, the problem of whether the number of points on the CM-curve is N+1-U or N+1+U is now almost completely solved. For D=3,4, this follows from a theorem by Katre. For h=1, see [14]. For D=20, see [16]. A recent paper by Stark [19] settles the case (D,6)=1. We have recently solved, using new invariants, the case D º 0 mod 3, and partially solved the cases D º ± 1 mod 3 [18]. As a consequence, one no more needs to compute [p+1± t]P to find the exact cardinality of the curve.

Several implementation tricks have also be added: trial divisions steps have been improved, and I/O have been drastically reduced. The use of Montgomery's arithmetic has allowed a speedup by a factor of 2. Berlekamp's algorithm (which is used to factor the polynomial HD over the field Fp) has been adapted according to an idea of Atkin: Classically, one splits the polynomial P over Fp by computing gcd(P(X), X(p-1)/2± 1). If small factors of p-1 are known, we can take a d-th root of unity zd, and compute gcd(P(X), X(p-1)/d - zdi) for all 0£ i < d. Instead of splitting the polynomial into two parts of degree roughly half of the initial polynomial, this should split it into several parts of smaller degree. Since our goal is just to find one linear factor, this should be much better, and indeed it is. This variant of Berlekamp's algorithm proved to be extremely efficient. Finally, backtrack was implemented at the request of E. Mayer, to allow one to restart interrupted computations. The current publicly available version of ECPP1 is v.5.6.1 which, though newer than the one in MAGMA, for instance, does not include any of the improvements or the tricks described above. The up-to-date version is version 6.4.5, currently unstable.

4.2   Records

Large primes proved to be prime by using ECPP software include the following ``world records'': However, the record is now the property of P. Mihailescu, using cyclotomy-based tests.

5   Conclusion

ECPP now seems to have reached a ``stable'' stage, where most of the theoretical problems with a real algorithmic pertinence have been solved, and the code has been cleaned and speeded up.

Perspectives include exploration of higher genus (à la Adleman-Huang). The main trouble is that the theory of complex multiplication is much more complicated in higher genus, and lots of practical problems arise when studying curves of genus ³ 2.

Another direction of exploration which needs further development is to try to make the best two primality tests (ECPP and cyclotomy) interact with each other, for instance through the concept of ``dual pairs'', i.e., couple of integers (p,q) together with an elliptic curve E defined over Z such that #E(Fp)=q and #E(Fq)=p.

References

[1]
Adleman (L. M.) and Huang (M.-D. A.). -- Primality testing and Abelian varieties over finite fields. -- Springer-Verlag, 1992, Lecture Notes in Mathematics, vol. 1512.

[2]
Adleman (L. M.), Pomerance (C.), and Rumely (R.). -- On distinguishing prime numbers from composite numbers. Annals of Mathematics, vol. 117, n°1, 1983, pp. 173--206.

[3]
Arno (Steven). -- A note on Perrin pseudoprimes. Mathematics of Computation, vol. 56, n°193, January 1991, pp. 371--376.

[4]
Atkin (A. O. L.) and Morain (F.). -- Elliptic curves and primality proving. Mathematics of Computation, vol. 61, n°203, July 1993, pp. 29--68.

[5]
Atkin (A. O. L.) and Morain (F.). -- Finding suitable curves for the elliptic curve method of factorization. Mathematics of Computation, vol. 60, n°201, January 1993, pp. 399--405.

[6]
Bosma (W.). -- Primality testing using elliptic curves. -- Technical Report n°85-12, Math. Institut, Universiteit van Amsterdam, 1985.

[7]
Chudnovsky (D. V.) and Chudnovsky (G. V.). -- Sequences of numbers generated by addition in formal groups and new primality and factorization tests. Advances in Applied Mathematics, vol. 7, 1986, pp. 385--434.

[8]
Cohen (H.) and Lenstra, Jr. (H. W.). -- Primality testing and Jacobi sums. Mathematics of Computation, vol. 42, n°165, 1984, pp. 297--330.

[9]
Cohen (Henri). -- A course in computational algebraic number theory. -- Springer-Verlag, Berlin, 1993, Graduate Texts in Mathematics, vol. 138, xii+534p.

[10]
Goldwasser (S.) and Kilian (J.). -- Almost all primes can be quickly certified. In Proc. 18th STOC. pp. 316--329. -- ACM, 1986. May 28--30, Berkeley.

[11]
Gordon (D. M.). -- Pseudoprimes on elliptic curves. In Koninck (J.-M. De) and Levesque (Claude) (editors), Théorie des nombres. pp. 290--305. -- Walter de Gruyter, 1989. Proceedings of the International Number Theory Conference held at Université de Laval, July 5--18, 1987.

[12]
Grantham (J.). -- Frobenius pseudoprimes. -- May 1996. Preprint.

[13]
Gurak (S.). -- Pseudoprimes for higher-order linear recurrence sequences. Mathematics of Computation, vol. 55, n°192, October 1990, pp. 783--813.

[14]
Joux (A.) and Morain (F.). -- Sur les sommes de caractères liées aux courbes elliptiques à multiplication complexe. Journal of Number Theory, vol. 55, n°1, November 1995, pp. 108--128.

[15]
Lenstra (H. W.). -- Primality testing algorithms (after Adleman, Rumely and Williams). In Bourbaki Seminar, Vol. 1980/81. Lecture Notes in Mathematics, pp. 243--257. -- Springer-Verlag, 1981.

[16]
Leprévost (F.) and Morain (F.). -- Revêtements de courbes elliptiques à multiplication complexe par des courbes hyperelliptiques et sommes de caractères. Journal of Number Theory, vol. 64, 1997, pp. 165--182.

[17]
Mihailescu (P.). -- Cyclotomy primality proving -- recent developments. -- March 1998. To appear in the Proceedings of ANTS-III.

[18]
Morain (F.). -- Primality proving using elliptic curves: an update. -- January 1998. To appear in the Proceedings of ANTS-III.

[19]
Stark (H. M.). -- Counting points on cm elliptic curves. Rocky Mountain Journal of Mathematics, vol. 26, n°3, 1996, pp. 1115--1138.
1
Available from http://www.lix.polytechnique.fr/Labo/Francois.Morain
This document was translated from LATEX by HEVEA.