Sorted and/or Sortable Permutations

Mireille Bousquet-Mélou

LaBRI, Université de Bordeaux

Algorithms Seminar

June 8, 1998

[summary by Cyril Banderier]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

1   Introduction

The classical railroad cars switching problem [12] (viz. to reorder cars in a given order with the help of a single garage-track) is here revisited and generalised in terms of permutations and trees. Permutations which are sortable by one (or more than one) stack have been studied by West [14] and some generating functions have been found [15]. By factorising permutations (following and generalising an idea of Zeilberger's), Mireille Bousquet-Mélou obtained functional equations for one-stack sortable, two-stack sortable, sorted permutations, sorted and sortable permutations. She shows q-analogues arise in counting inversions. Most of these functional equations involve divided differences. The quadratic method allows to solve some of them while the other ones remain quite mysterious. She also gives an algorithm which decides if a permutation is sorted.

2   Sorting Procedure

In his Ph.D. thesis [14], Julian West studied a procedure P that permutes the letters of a word s consisting of distinct letters in the alphabet {1,2,3, ... }. The procedure uses a stack s and works as follows:

In this procedure, e is the empty word, s~ is the mirror of the word s and the inverse b-1 of a letter b of the alphabet {1,2,3, ... } is a new letter with the property b b-1=b-1 b = e. The output word t has n letters, and we define it to be P(s), the word obtained by sorting s through a stack. This procedure extends a procedure described by Knuth [12, p. 238].

West observed that the map P can alternatively be described recursively by
P (sL m sR) =P(sL)P (sR)m
where m is the largest letter of the word s = sL m sR. With at most n-1 iterations, s is an increasing word, i.e. P sorts the letters of s.


Figure 1: The sorting algorithm applied to s=2351674.

Let Sn be the set of permutations of {1,2,...,n}. We represent the action of P on Sn by a sorting tree: the nodes of this tree are the elements of Sn, and an edge connects s to P(s) for all s Î Sn.


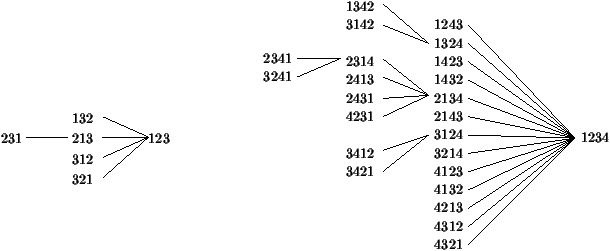
Figure 2: The sorting trees for S3 and S4.

We can visualise on this tree the four classes of permutations we will consider in this paper.

One-stack sortable permutations
These permutations occur in the last two columns of the sorting tree. Knuth [12] proved that the number of such permutations is (
2n
n
) /(n+1). They are exactly the permutations avoiding the pattern 231: there exists no triple (i,j,k) with 1£ i<j<k£ n such that s(k)<s(i)<s(j).

Two-stack sortable permutations
They occur in the last three columns of the sorting tree. Their generating function å cn xn satisfies
x2F3+x(2+3x)F2+(1-14x+3x2)F+x2+11x-1=0.
West conjectured that
cn=
2(3n)!
(2n+1)!(n+1)!
.
This was proved by Zeilberger [15], who found the previous equation and then used the Lagrange inversion formula.

Sorted permutations
These are those permutations which belong to P( Sn). Induction on the length of permutations shows that any suffix of a sorted permutation is a sorted word. Sorted permutations cannot be described in terms of forbidden patterns: in fact any pattern occurs as a factor in some sorted permutation. We shall give a functional equation satisfied by their generating function.

Sorted and (one-stack) sortable permutations
Their generating function satisfies
x3 F4+x2(3+4x)F3+x(3-29x+6x2)F2+(1-7x+29x2+4x3)F-(1-x)3=0.

3   Permutations and Trees

There is a classical bijection between permutations and binary search trees: one gets a permutation from a labelled tree by reading it with a ``lower reading'' (you start at the root, and recursively, you read the subtrees, the left one at first, and when you have visited all the left children, you add the label of the current node to a list, the final list is the permutation associated to the tree), on the other hand one gets a tree from a permutation s=sL m sR by creating recursively the tree with root m and a left subtree associated to sL and a right subtree associated to sR.

We will now show on an example an algorithm that decides whether a permutation is sorted and, if it is indeed sorted, gives the pre-image. Beginning with t = 6.3.11.1.4.5.2.7.9.8.10.12 Î S12, one splits it after each descent: 6 | 3.11 | 1.4.5 | 2.7.9 | 8.10.12 then one reads it from right to left, and for each factor one creates the associated tree where the root is the maximum and each node has only a right child. One gets then fives trees (12,10,8), (9,7,2), (5,4,1), (11,3) and (6). And finally one tries to create the associated binary search tree, which is possible if and only if t is sorted. What is more, by noting s the word given by a ``lower reading'' of the final tree, we get t= P(s). With our example, we have t= P(6.11.3.12.9.5.4.1.7.2.10.8) is sorted.

4   Notations

The number of 23 1 patterns in a permutation s is the number of pairs (i,k) with i<k such that there exists j Î [i, k] with s(k)<s(i)<s(j). Note that the number of 23 1 patterns in a permutation s, denoted below INV (s), is the number of inversions of P(s). For instance, the permutation s of Fig. 1 has four 2 3 1 patterns (corresponding to the pairs of letters (2,1), (3,1), (5,4) and (6,4)) and P(s) has four inversions (given by the same pairs of letters). For s Î Sn, we define z(s) by the largest l such that n occurs before n-1 and n-1 occurs before n-2 and ··· and n-(l -2) occurs before n-(l-1)}. For instance, z(519268374)=3. For m,n ³ 0, we define the sets Sm,n and Sm,n by
Sm,n = { s Î Sm+n : z(s) ³ n }     and    
S
m,n = { s Î Sm+n : z(s) = n }.

Let s Î Sm,n and s=sL m sR, we note m' the largest letter of sR, so we have the factorisation s=A m' B. It is this factorisation which allowed the author to find equations verified by the generating functions. We will use the usual notations [n]=1+q+... + qn-1=1-qn/1-q and [n]!=[1][2] ··· [n]. Let C be a set of permutations. By the ordinary (resp. exponential) generating function of C we mean the series
C(x,y)=
 
å
m, n ³ 0
cm,nxmyn,     resp.    C(x,y)=
 
å
m, n ³ 0
cm,n
xm
m!
yn,
where cm,n is the number of permutations s of C of length m+n such that z(s) ³ n. The ordinary (resp. Eulerian) INV-generating function of C is
C(x,y;q)=
 
å
m, n ³ 0
cm,nxmyn,     resp.    C(x,y;q)=
 
å
m, n ³ 0
cm,n
xm
[m]!
yn,
where cm,n=ås Î C Ç Sm,n qINV(s). The definition for the inv-generating function of C is similar.

5   Functional Equations

Proposition 1   The Eulerian INV-generating function A(x,y;q) for general permutations is completely characterised by the initial condition A(0,y;q)=1/(1-y) and the equation
A(x,y;q)- A(xq,y;q)
x(1-q)
= [ 1+y A(xq,y;q) ]
A(x,y;q)- A(x,0;q)
y
.
In the limit q® 1, we find, for the series A(x,y), the initial condition A(0,y)=1/(1-y) and the equation
A
x
(x,y) = [ 1+yA(x,y) ]
A(x,y)-A(x,0)
y
.

Proposition 2   The ordinary generating function B(x,y) for one-stack sortable permutations is completely characterised by the equation
B(x,y)=
1
1-y
+
x
1-y
B(x,y)-B(x,0)
y
.

Proposition 3   The ordinary INV-generating function C(x,y) for two-stack sortable permutations is completely characterised by the equation
C (x,y;q) =
1
1-y
+ x [ 1+y C(xq,y;q) ]
C(x,y;q)- C(x,0;q)
y
.

Proposition 4   The Eulerian inv-generating function D(x,y;q) for sorted permutations is completely characterised by the initial condition D(0,y;q)=1/(1-y) and the equation
D(x,y;q)- D(xq,y;q)
x(1-q)
=(1-y) [ 1+y D(xq,y;q) ]
D(x,y;q)- D(x,0;q)
y
.
In the limit q® 1, we obtain for the exponential generating function D(x,y) the initial condition D(0,y)=1/(1-y) and the equation
D
x
(x,y) =(1-y) [ 1+yD(x,y) ]
D(x,y)-D(x,0)
y
.

Proposition 5   The ordinary inv-generating function E(x,y;q) for sorted and sortable permutations is completely characterised by the equation
E (x,y;q) =
1
1-y
+ x(1-y) [ 1+y E(xq,y;q) ]
E(x,y;q)- E(x,0;q)
y
.

Remarks
The ordinary length generating function B(x,0) for one-stack sortable permutations can be solved by the kernel method. The equations of Propositions 3 (two-stack sortable permutations) and 5 (sorted and sortable permutations) can be solved when q=1 via the so-called quadratic method, which is due to Brown [6, section 2.9.1]. There is no known q-analogue of this method! On the other hand, the equations for the general permutations and for sorted permutations can be ``solved'' as we will see in the next section.

6   Solving Equations with a q-Derivative

Both equations are of the following form:
F
x
(x,y) =c(y) [ 1+yF(x,y) ]
F(x,y)-F(x,0)
y
,     (1)
where c(y)=1 for general permutations and c(y)=1-y for sorted permutations.

One uses the two following results in order to ``solve'' these equations.
Lemma 1  [Bernoulli linearisation]   Let F(x,y) Î R(y)[[x]] be defined by the initial condition F(0,y)=1/(1-y) and Eq. (1), with c(y)=1 or c(y)=1-y. Let G(x,y) be the following series of R(y)[[x]]:
G(x,y)=
1
c(y) [ 1+yF(x,y) ]
.
Then G(0,y)=(1-y)/c(y) and
y
G
x
(x,y)-c(y) [ 1+yF(x,0) ] G(x,y)+1=0.
Most importantly, G(x,y) has polynomial coefficients in y, i.e., G(x,y) Î R[y][[x]].

Lemma 2  [Laplace transform]   Let h(x,y) Î R[y][[x]] be a formal series in x with polynomial coefficients in y. Let G(x,y) be the series of R(y)[[x]] defined by an initial condition G(0,y) Î R(y) and the differential equation:
y
G
x
(x,y)- [ 1+yh(x,y) ] G(x,y)+1=0.
Let
H(x,y) = exp é
ê
ê
ê
ê
ë		 - ó
õ
x


0
h(u,y) d u ù
ú
ú
ú
ú
û		 =
 
å
i³ 0
Hi(y)
xi
i!
.
Then the coefficients of G(x,y) are polynomials in y if and only if G(0,y)Î R[y] and
 
å
i³ 0
Hi(y) yi=G(0,y).
In other words, the Laplace transform of H(x,y) with respect to x is exactly G(0,y) when evaluated at x=y:
1
y
ó
õ
¥


0
e-u/yH(u,y) d u =G(0,y).

For general permutations, with c(y)=1, one gets
F(x,y)=A(x,y) =
1
1-x-y
.

For sorted permutations, with c(y)=1-y, the series F(x,y) is the exponential generating function D(x,y) for sorted permutations. The series G(x,y)=1/[ (1-y) (1+yD(x,y))] satisfies (1) with h(x,y)=(1-y)D(x,0)-1. Moreover, G(0,y)=1. With the notations of Lemma 2, we have:
H(x,y)=exp(x+(y-1) D (x))
where
D (x) = ó
õ
x


0
D(u,0)du.
Lemma 2 gives the following result.

Proposition 6   Let
D (x) =
 
å
m³ 0
dm,0
xm+1
(m+1)!
where dm,0 is the number of sorted permutations of length m. Then the series D(x) is completely characterised by the following equation:
1-y
y
ó
õ
¥


0
e-u(1-y)/y exp [ (y-1) D (u) ] du = 1-y.
In other words, let K (x,y)= exp [ (y-1) D (x)]=åi³ 0 Ki(y) xi / i!, and let K^ (x,y)= åi³ 0 Ki(y) xi be its Laplace transform with respect to x. Then
^
K
 
æ
ç
ç
è
y
1-y
, y ö
÷
÷
ø		 = 1-y,     or, equivalently   
^
K
 
æ
ç
ç
è		 u,
u
1+u
ö
÷
÷
ø		 =
1
1+u
.

The first coefficients of the series are 1,1,2,5,17,68,326,1780,11033,76028,578290,4803696. One does not know if this series is algebraic, D-finite,...Thus, the generating function for sorted permutations remains mysterious. Mireille Bousquet-Mélou will give a solving method for the full q-analogue equations in a for coming paper.

References

[1]
Barcucci (Elena), Del Lungo (Alberto), Lanini (S.), Macrí (M.), and Pinzani (Renzo). -- The inversion number of some permutations with forbidden subsequences. Proceedings of SOCA'96 Tianjin, 1996, pp. 21--32.

[2]
Bousquet-Mélou (Mireille). -- A method for the enumeration of various classes of column-convex polygons. Discrete Mathematics, vol. 154, n°1-3, 1996, pp. 1--25.

[3]
Bousquet-Mélou (Mireille). -- Multi-statistic enumeration of two-stack sortable permutations. Electronic Journal of Combinatorics, vol. 5, n°1, 1998.

[4]
Bousquet-Mélou (Mireille). -- Sorted and/or sortable permutation. Preprint, LaBRI, 1998.

[5]
Brown (William G.). -- Enumeration of quadrangular dissections of the disk. Canadian Journal of Mathematics, vol. 17, 1965, pp. 302--317.

[6]
Brown (William G.). -- On the existence of square roots in certain rings of power series. Mathematische Annalen, vol. 158, 1965, pp. 82--89.

[7]
Brown (William G.). -- On the enumeration of non-planar maps. Memoirs of the American Mathematical Society, vol. 65, 1966, p. 42.

[8]
Brown (William G.) and Tutte (William Thomas). -- On the enumeration of rooted non-separable planar maps. Canadian Journal of Mathematics, vol. 16, 1964, pp. 572--577.

[9]
Cori (Robert), Jacquard (B.), and Schaeffer (Gilles). -- Description trees for some families of planar maps. In Formal Power Series and Algebraic Combinatorics, pp. 196--208. -- 1997. Proceedings of the 9th Conference, Vienna.

[10]
Cori (Robert) and Richard (Jean). -- Énumération des graphes planaires à l'aide des séries formelles en variables non commutatives. Discrete Mathematics, vol. 2, 1972, pp. 115--162.

[11]
Dulucq (Serge), Gire (S.), and West (Julian). -- Permutations with forbidden subsequences and nonseparable planar maps. Discrete Mathematics, vol. 153, n°1-3, 1996, pp. 85--103.

[12]
Knuth (Donald E.). -- The Art of Computer Programming. -- Addison-Wesley, 1973, vol. 1.

[13]
Rawlings (Don). -- The Euler-Catalan identity. European Journal of Combinatorics, vol. 9, n°1, 1988, pp. 53--60.

[14]
West (Julian). -- Permutations with restricted subsequences and stack-sortable permutations. -- PhD thesis, MIT, 1990.

[15]
Zeilberger (Doron). -- A proof of Julian West's conjecture that the number of two-stack-sortable permutations of length n is 2(3n)!/((n+1)!(2n+1)!). Discrete Mathematics, vol. 102, n°1, 1992, pp. 85--93.
This document was translated from LATEX by HEVEA.