Minimal Decomposition and Computation of Differential Bases for an Algebraic Differential Equation

Évelyne Hubert

LMC, Grenoble

Algorithms Seminar

September 21, 1996

[summary by Bruno Salvy]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract
Singular and general solutions of algebraic differential equations can be expressed in a differential algebra setting regardless of the existence of closed-form. Theoretical and algorithmic tools in this area are presented.



1   Types of solutions

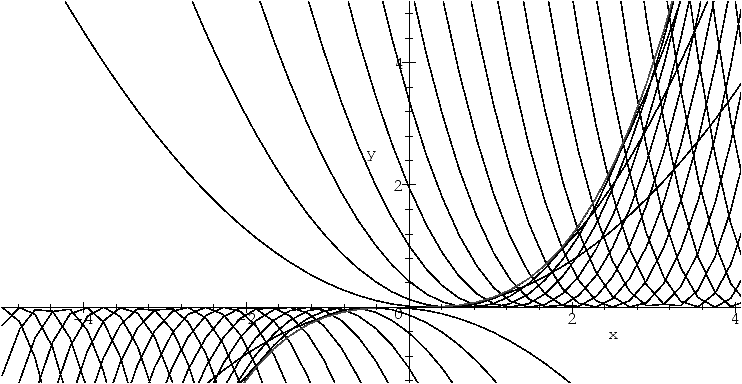
Consider the following differential equation:
y'3-4xyy'+8y2=0.     (1)
This equation admits three solutions of different types:
y(x)=a(x-a)2,     y(x)=0,     y(x)=
4
27
x3.     (2)
The first one is the general solution and the two other ones are singular solutions. The solution y(x)=0 is actually a special case of the general solution and is called a particular singular solution; the third one is an essential singular solution. As showed by Figure 1, both singular solutions appear as envelopes of the general solution. In general, this is true of essential singular solutions of first order equations.


Figure 1: Solutions of (1)

In the general case of an equation
P(x,y,y',...,y(n))=0,
where P is a polynomial, the singular solutions are the simultaneous solutions of P and its separant  P/ y(n). Through differential algebra, a meaning can also be given to the ``general'' solution even when no closed-form exists. It is also possible to distinguish algebraically between a particular singular solution and an essential one. The aim of É. Hubert's work is to provide algorithms dealing with general and singular solutions in this framework.

To an ordinary differential equation like (1) is associated a differential polynomial
p=y13-4xy0y1+8y02ÎQ(x){y}.
More generally, the differential ring A=A{y} is a ring of polynomials in the variables y0,y1,y2,... endowed with an operator d which is a derivation on the commutative integral domain A and which is such that d yi=yi+1. A differential ideal is an ideal stable under d. For instance the differential ideal generated by a differential polynomial p is the polynomial ideal generated by p and its derivatives:
[p]=(p,d p,d2p,...).
Of particular interest is the radical of this ideal:
{p}=([p])1/2={aÎA| $ kÎN, akÎ[p]}.
This is the set of differential polynomials vanishing on all the solutions of p. A differential ideal I is prime when abÎ IÞ aÎ I or bÎ I.

We now restrict to A=Q(x) for simplicity, but the results can be stated in much more generality, see [4, 5]. An important property is that a radical differential ideal R can be decomposed into a finite intersection of prime differential ideals:
R=
r
Ç
k=1
Pk.
When none of the Pk is included in another one, this decomposition is called minimal and is unique. These Pk's are then called essential components of R. In the same way as {p} corresponds to the solutions of p, each of the essential components of {p} corresponds to one type of solutions of p. In the same example as before, a decomposition is
{p}={p,y22-2xy2+2y1,y3}Ç{y0}Ç{27y0-4x3},
each term corresponding to one of (2). This decomposition is not minimal since the second ideal obviously contains the first one and therefore corresponds to a particular singular solution. The minimal decomposition is obtained by removing this second term. Testing the inclusion of the general component (the first one here) into one of the other ones is related to Ritt's problem; its algorithmic resolution via the computation of a differential basis of each component is one of the aims of [3].

While the singular solutions obviously correspond to components of the ideal {p,s}, where s is the separant of p, the general solution corresponds to the quotient of {p} by s, where the quotient of a radical differential ideal R by an element sÎA is defined as
R:s={aÎA| saÎ R},
which is itself a radical differential ideal. Two properties are of interest: for any non-empty subset s of A, one has {s}={s}:sÇ{s,s}; when p is irreducible as a polynomial in y0,y1,... and s is its separant, the ideal {p}:s is prime. Thus  Gp={p}:s is an essential component of {p} which is called the general component of p.

2   Algorithms for minimal decompositions

We now turn to the actual computation of the minimal decomposition
{p}= GpÇ R1Ç...Ç Rk.
Ritt showed that each essential component Ri is the general component of some differential polynomial ai. The computation of a minimal decomposition then requires finding these ai's and insuring that the decomposition is minimal.

Ritt's low power theorem states that when an irreducible differential polynomial p of a differential ring A{y1,...,yn} is contained in one of the ideals {yi}, then {yi} is an essential component of {p} if and only if the lowest degree terms of p do not contain a derivative of yi. This theorem can be used to give a criterion for a  Ga to be an essential component of {p} after a preparation process which rewrites p as a differential polynomial in a:
sakp=
 
å
a0,...,ae
c
 
a0,...,ae
a
a0
 
0
··· a
ae
 
e
,
where sa is the separant of a, ai=di a, ca0,...,aeÏ Ga and e is the difference between the order n of p and the order m of a. This reduction process is performed in three stages: for i from 1 to e, ai=d ai-1 can be rewritten ai=saym+i+ti for some ti. Then yn is replaced by (ae-te)/sa in p. After normalization this yields
s
ke
 
a
p=å
c
 
ae
a
ae
 
e
,
where the coefficients do not involve derivatives higher than yn-1. The process is then repeated with the yn-i in succession. This rewrites all the ym+i for i>0. Then in each monomial caa1a1··· aeae, the coefficient ca is rewritten c~aa0a0, where a0 is the largest integer k such that ak divides ca.

In our previous example, the reduction of p in terms of y0 is tautologous; the lowest degree terms of p is -4xy0y1+8y02 and thus {y0} is not an essential component. The reduction of p in terms of a=27y0-4x3 is more interesting. The separant sa=27 is constant and the first step of the reduction process yields a1=27y1-12x2. Then p is rewritten successively
p =y13-4xy0y1+8y02,
19683p =a13+36x2a12-108x(27y0-4x3)a1+216(27y0-2x3)(27y0-4x3),
19683p =a13+36x3a12-108xa0a1+216(27y0-2x3)a0.
The lowest degree term is 216(27y0-2x3)a0 which does not involve a1 and thus {27y0-4x3} is an essential component. (There also exists a simpler algorithm in this case since p is of order 1 [2]).

The computation of the ai's relies on the Rosenfeld-Gröbner algorithm [1] which has been implemented in Maple by F. Boulier. Given a system S of differential polynomials and a ranking, this algorithm computes a decomposition of the radical ideal {S} as a finite intersection of radical differential ideals:
{S}= I1Ç...Ç Is,
each  Ii being described by a system of polynomial equations and inequations and a characteristic set. This decomposition makes it possible to test membership in the  Ii's and therefore in {S} by simple reductions. Note that the  Ii's are not necessarily prime.

A lemma of Lazard's combined with Ritt's result mentioned above shows that the  Ii's corresponding to essential components of {p,s} must have a characteristic set reduced to one differential polynomial. This makes it possible to filter out some of the radical ideals. Then prime differential ideals can be obtained by factorization. This leads to the following algorithm.
Input: An irreducible differential polynomial p.
Output: a1,...,ar such that  Gp, Ga1,..., Gar are the essential components of {p}.
G:=Rosenfeld-Gröbner([p,s]);
A:=[];
for each R in G with cardinality 1 do
In our example, the output of Rosenfeld-Gröbner is
{y0},    {27y0-4x3},
from where the computations above have been performed.

It is possible to avoid the factorization and perform only gcd computations. In some cases, this algorithm can also be extended to compute a differential basis of  Gp. This is helpful to compute power series solutions when the initial conditions lie on a singular solution. We refer to [3] for details.

References

[1]
Boulier (F.), Lazard (D.), Ollivier (F.), and Petitot (M.). -- Representation for the radical of a finitely generated differential ideal. In Levelt (A. H. M.) (editor), Symbolic and Algebraic Computation. pp. 158--166. -- New York, 1995. Proceedings of ISSAC'95, July 1995, Montreal, Canada.

[2]
Hubert (Évelyne). -- The general solution of an ordinary differential equation. In Lakshman (Y. N.) (editor), Symbolic and Algebraic Computation. pp. 189--195. -- New York, 1996. Proceedings ISSAC'96, Zürich, July 1996.

[3]
Hubert (Évelyne). -- Étude algébrique et algorithmique des singularités des équations différentielles implicites. -- PhD thesis, Institut National Polytechnique de Grenoble, April 1997.

[4]
Kolchin (E. R.). -- Differential algebra and algebraic groups. -- Academic Press, New York, 1973, Pure and Applied Mathematics, vol. 54, xviii+446p.

[5]
Ritt (Joseph Fels). -- Differential Algebra. -- American Mathematical Society, New York, N. Y., 1950, American Mathematical Society Colloquium Publications, vol. XXXIII, viii+184p.
This document was translated from LATEX by HEVEA.