On the Group of a Sandpile

On the Group of a Sandpile

Dominique Rossin

Lix, École polytechnique (France)

Algorithms Seminar

October 16, 2000

[summary by Dominique Gouyou-Beauchamps]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract

The abelian sandpile model is a cellular automaton. Its rules generalize the sandpile rules for general graphs. This model has been introduced by Bak, Tang, and Wiesenfeld [1] in 1987. Dhar [9] showed that the set of recurrent configurations of this automaton has the structure of a finite abelian group.

In this talk, we describe several algorithms to determine the identity in the group. This element presents fractal aspects that we are not able yet to explain. These algorithms allow us to introduce relationships between the sandpile group and well-known algebraic or combinatorial objects.

Details may be found in the recent works of R. Cori, D. Rossin, and B. Salvy [6], and D. Rossin [12]. The papers [1, 10], the book [2], and the thesis [13] are good introductions to sandpiles.

1 Introduction

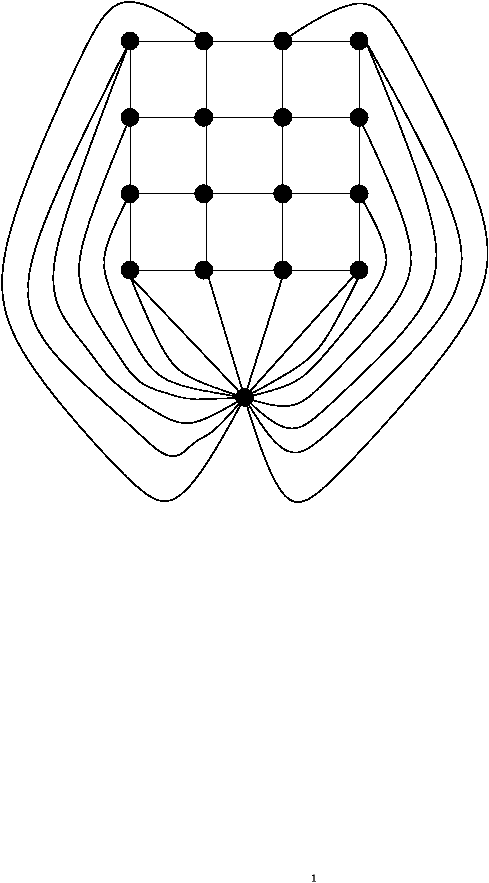
Let G=(V,E) be a non-oriented and connected multi-graph with V={1,...,n} its set of vertices and E a symmetric n× n matrix whose entry e_i,j is the number of edges with endpoints i, j. It is assumed that for any i, e_i,i=0 so that the multi-graph has no loops. Frequently, G is a graph, and hence e_i,j is either 0 or 1. The degree of vertex i in G is d_i=å_j=1ⁿe_i,j. A multi-graph is rooted if one of its vertices is distinguished, it is called the sink and is numbered n.

A configuration u=(u₁,...,u_n)ÎNⁿ of G is a vector of non-negative integers. In the context of the sandpile model, the vertices of the graph are cells, and the number u_i may be interpreted as the height of a pile of grains of sand standing in cell i. In the rest of this talk, the number of grains in the sink is not taken into account. Thus two configurations u and v which differ only in position n are considered as equal; we write u=v if u_i=v_i for all 1£ i<n. This translates the fact that the sink collects all grains of sand getting out of the system.

A toppling of the vertex i, 1£ i<n, in configuration u consists in decreasing the number of grains in this vertex by its degree while the number of those of each of its neighbours j increases by e_i,j. This is equivalent to the addition to u of the vector D_i such that (D_i)_i=-d_i and (D_i)_j=e_i,j for j¹ i. The notation u¾® v means that v is obtained from u by toppling a vertex, so that there exists an 1£ i<n such that v=u+D_i. The transitive closure of the toppling operation ¾® is denoted

¾®

: u

¾®

v if v is obtained from u by a sequence of topplings. An avalanche is a sequence of topplings (see Figures 1, 2 and 3).

The sandpile model has been introduced by Bak, Tang, and Wiensenfeld [1] in 1987. In a recent book, Bak [2] gives an overview of many physical problems---earthquakes and solar flares for example---whose models are based on the sandpile one. All these models follow the Gutemberg--Richter law: logN=a-bM, logE=c+dM, and N~ E^1-t (t»2) where M is the magnitude, N is the number of topplings, and E is the energy. In three dimensions, N~ E^1-t (t» 2.5). A very similar automaton was introduced independently by other authors under the name of the chip-firing game [4, 11]. Biggs [3] found many algebraic and combinatorial properties of the chip-firing game, some of which correspond to Dhar's results on sandpiles [10]. In [5], we also showed a close relationship between recurrent configurations of the complete graph and the parking functions.

Figure 1: Multi-graph corresponding to the 4×4 grid.

Figure 2: Topplings and avalanche on the 4×4 grid.

Figure 3: Topplings and avalanche on a graph.

2 The Sandpile Group

A vertex is stable if it contains a number of grains less than its degree, otherwise this vertex is unstable. A stable configuration is a configuration where all vertices are stable. It is not difficult to prove that for every configuration u there exists a stable configuration u^{^} such that u

¾®

u^{^}. Moreover this configuration is unique, and the number of topplings is independent of the way in which u^{^} is obtained from u [9].

Let u, v be two configurations. Let u_i (resp. v_i) be the number of grains on vertex i in configuration u (resp. v). We will denote by u+v the configuration w such that w_i=u_i+v_i. A configuration u is recurrent if it is stable and if there exists a configuration v¹0 such that u+v

¾®

u (see Figure 4). The simplest example of a recurrent configuration is d=(d₁-1,d₂-1,...,d_n-1-1,0). The set of recurrent configurations is isomorphic to the set of equivalence classes defined by the symmetric closure º of

¾®

.

Let T_G(x,y) be the Tutte polynomial of the graph G. Then T_G(1,y) is the the generating function (a polynomial) of the recurrent configurations according to the number of sand grains.

We can associate to the set of recurrent configurations the operator Å defined by uÅ v=u+v^{^} where u and v are two recurrent configurations. The set of recurrent configurations with the operation Å is an abelian group G [8], this group is equal to the product G=Õ_i=1ⁿZ/d_iZ and the group structure does not depend on the sink choice in the graph G.

Let u=(u₁,...,u_n) be a recurrent configuration. We denote u^_ the recurrent configuration (d₁-1-u₁,d₂-1-u₂,...,d_n-1-1-u_n-1,0). Then the identity of the sandpile group is Id=dÅ(dÅd) and the opposite of a recurrent configuration u is IdÅ(dÅ u).

Figure 4: A recurrent configuration.

3 Toppling Ideal, Set Topplings and Minimal Gröbner Basis

Configurations and topplings are easily translated from the linear algebra setting into polynomial operations by associating to a configuration u=(u₁, u₂,..., u_n)ÎNⁿ a monomial x_u=x₁^u₁x₂^u₂... x_n^u_n Î Q[x₁,...,x_n]. To a toppling D_i is associated the binomial T(x_i)=x_i^d_i-Õ_jx_j^e_i,j. The addition of two configurations translates into the multiplication of the corresponding monomials and toppling vertex i in u translates into the division of x_u by x_i^d_i followed by the multiplication by Õ_j=1ⁿx_j^e_i,j. We define the toppling ideal I_G as the ideal generated by x_n-1 and the toppling polynomials T(x_i) for iÎ{1,...,n}.

A toppling polynomial can also be associated to a subset X of the set V of vertices as follows. For a vertex i of V, define

d_i(X)=

jÎ X

e_i,j,

the number of edges with endpoints i and a vertex of X. The set toppling of the set X in configuration u consists in adding the vector D_X to u, where

(

D_X

)

_i=

ì
ï
í
ï
î

-d_i(

for iÎ X,

d_i(X),

for iÎX^_,

where X^_ denotes V\ X.

Accordingly, the toppling polynomial of the subset X of V is defined by

T(X)=

iÎ X

d_i(

)

iÎ

x_i^d_i(X).

Gröbner bases are a classical computational tool for dealing with polynomial ideals. Given an ordering on monomials which is compatible with the product (a so-called admissible ordering) and a set of generators of an ideal I, one can compute a Gröbner basis for I and from there test ideal membership and more generally compute normal forms in the quotient of the algebra by I. The rest of this work makes use of the notation and basic results from [7, Chapter 2].

The graded reverse lexicographic order (grevlex) denoted <, is defined as follows. If A=Õ_i=1ⁿx_i^{a _i} and B=Õ_i=1ⁿx_i^{b _i} are two monomials in the variables x_i, i=1,2,...,n, then A< B if

|a |=

i=1

a_i<|b|=

i=1

b_i

or |a |=|b | and in (a₁,...,a_n)-(b₁,...,b_n) the right-most non-zero entry is positive.

From there a toppling order is defined as follows: let s be a permutation of {1,...,n} such that s (n)=n and if the distance from vertex i to the sink is larger than the distance from vertex j to the sink, then s (i)>s(j). The toppling order is the graded reverse lexicographic order on x_s(1), x_s(2), ..., x_s(n).

Theorem 1 A Gröbner basis of the ideal I_G with respect to a toppling order is given by

{

T(X)|XÌ{1,...,n}

}

È{x_n-1}.

A Gröbner basis is minimal when its elements have leading coefficient 1 and no leading monomial divides another leading monomial in the basis. A subset X of vertices of the graph G=(V,E) is well-connected if both subgraphs of G induced by X and X^_ are connected.

Theorem 2 The set S_c of toppling polynomials corresponding to the sets XÌ {1,2,...,n-1} which are well-connected is a minimal Gröbner basis for the toppling order.

In the worst case, the minimal Gröbner basis still contains 2^n-1 elements for the complete graph.

As mentioned before, the quotient Q[x₁,x₂,...,x_n]/I_G is a Q-vector space whose dimension is the order of the group of recurrent configurations. From a Gröbner basis for I_G, a basis of this vector space is given by the set of monomials that do not reduce to 0 by the basis. We call these reduced monomials. Theorem 3 below gives a simple bijection between reduced monomials for the toppling order and recurrent configurations.

Let F be the mapping from the set of stable configurations onto itself given by F(u)=d-u. We also denote F(M)=F(a₁,a₂,...,a_n) for a monomial M=x₁^a₁x₂^a₂... x_n^a_n.

Theorem 3 The mapping F defines a bijection between the set of reduced monomials with respect to the toppling order and the set of recurrent configurations.

For a configuration u, let r(u) denote the reduced configuration obtained from the monomial associated to u by performing reductions by the Gröbner basis of I_G associated with the toppling order.

Proposition 1 If u is a configuration then the recurrent configuration equivalent to u is

(

r(u)

)

The identity in the group of recurrent configurations is F(r(d)).

Corollary 1 For two recurrent configurations u and v,

uÅ v=F

(

F(u)+F(v)

)

Figure 5: Multigraph with 4 vertices.

Figure 6: Representation of irreducible monomials.

Proposition 1 yields the following algorithm to compute the identity on a graph G with sink s: beginning with the configuration d, perform the set topplings for all well-connected subgraph of G\{s} (this is equivalent to reducing by the Gröbner basis for the toppling order). When no further set toppling can be performed, for each cell i replace its number of grains n_i with d_i-n_i. The resulting configuration is the identity.

4 Examples

Our first example corresponds to the graph displayed on Figure 5. The structure of the graph is reflected by the toppling polynomials for the vertices:

x₁³-x₂²x₃, x₂³-x₁²x₄, x₃²-x₁x₄, x₄²-x₂x₃, x₄-1.

The minimal Gröbner basis for the graded reverse lexicographic order on monomials is

x₃²-x₁, x₂³-x₁², x₁³-x₂, x₂x₃-1, x₂x₁-x₃, x₃x₁²-x₂², x₄-1.

Apart from the last, these polynomials correspond respectively to well-connected subgraphs with vertices

{3}, {2}, {1}, {1,2,3}, {1,2}, {1,3}.

Given a Gröbner basis G={p₁,p₂,...,p_k}ÌK[x₁,x₂,...,x_n] for some field K, it is usual to represent the leading monomials of the p_i on an integer lattice in n dimensions. Each polynomial p is associated to a point c(p) whose coordinates are the exponents of its leading monomial. The leading terms of the p_i generate the ideal of leading terms of polynomials in the ideal. These leading terms are thus exactly represented by È c(p_i)+Nⁿ. This removes from Nⁿ a staircase shape whose lattice points correspond to the quotient (see Figure 6). Their number is exactly the order of the group of recurrent configurations. Note that in our example, those seven monomials are {1,x₁,x₁²,x₂,x₂²,x₃,x₁x₃}, none of which correspond to a recurrent configuration. However, applying F yields the recurrent configurations as explained above.

Our second example is the 2× 2 grid consisting of 4 cells, each connected twice to the sink. The sandpile group of this grid, computed for instance in [9], is the product of two cyclic group of orders 24 and 8.

After the computation of the Gröbner basis of the ideal generated by the toppling polynomials of vertices, it follows that x₄ is of order 24 and that any element can be expressed as a product x₃ⁱx₄^j where 0£ i£ 7 and 0£ j£ 23, which gives that the order of the group is 192. Also, since x₁ and x₂ can be expressed in terms of x₃ and x₄, it is seen that the group has two generators.

References

[1]: Bak (P.), Tang (C.), and Wiensenfeld (K.). -- An explanation of 1/f noise. Physical Review Letters, vol. 59, n°4, July 1987, pp. 381--384.
[2]: Bak (Per). -- How nature works. -- Copernicus, New York, 1996, xiv+212p. The science of self-organized criticality.
[3]: Biggs (N. L.). -- Chip-firing and the critical group of a graph. Journal of Algebraic Combinatorics, vol. 9, n°1, 1999, pp. 25--45.
[4]: Björner (Anders), Lovász (László), and Shor (Peter W.). -- Chip-firing games on graphs. European Journal of Combinatorics, vol. 12, n°4, 1991, pp. 283--291.
[5]: Cori (Robert) and Rossin (Dominique). -- On the sandpile group of dual graphs. European Journal of Combinatorics, vol. 21, n°4, 2000, pp. 447--459.
[6]: Cori (Robert), Rossin (Dominique), and Salvy (Bruno). -- Polynomial ideals for sandpiles and their Gröbner bases. -- Research Report n°3946, Institut National de Recherche en Informatique et en Automatique, 2000. 20 pages. Submitted to Elsevier Preprint.
[7]: Cox (David), Little (John), and O'Shea (Donal). -- Ideals, varieties, and algorithms. -- Springer-Verlag, New York, 1997, second edition, xiv+536p. An introduction to computational algebraic geometry and commutative algebra.
[8]: Creutz (M.). -- Abelian sandpile. Computers in Physics, vol. 5, 1991, pp. 198--203.
[9]: Dhar (D.), Ruelle (P.), Sen (S.), and Verma (D.-N.). -- Algebraic aspects of abelian sandpile models. Journal of Physics A, vol. 28, n°4, 1995, pp. 805--831.
[10]: Dhar (Deepak). -- Self-organized critical state of sandpile automaton models. Physical Review Letters, vol. 64, n°14, 1990, pp. 1613--1616.
[11]: Goles (Eric). -- Sand piles, combinatorial games and cellular automata. In Instabilities and nonequilibrium structures, III (Valparaíso, 1989), pp. 101--121. -- Kluwer Acad. Publ., Dordrecht, 1991. Vol. 64 in Mathematics and its Applications.
[12]: Rossin (D.). -- On the complexity of addition in the sandpile group of a graph. -- Submitted to Elsevier Preprint.
[13]: Rossin (D.). -- Propriétés combinatoires de certaines familles d'automates cellulaires. -- Thèse, École polytechnique, Palaiseau, France, 2000.

This document was translated from L^AT_EX by H^EV^EA.