Cover Time and Favourite Points for Planar Random Walks

Amir Dembo

Mathematics and Statistics Department, Stanford University (USA)

Algorithms Seminar

June 18, 2001

[summary by Christine Fricker  Pierre Nicodème]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).
Abstract
In this talk, Amir Dembo considers random walks on Z2 and presents a proof of the Erdös--Taylor conjecture related to frequently covered points. The Kesten--Révész conjecture on the covering time of the two-dimensional torus Zn2=Z2/nZ2 is also solved. These results are a common work of Amir Dembo, Yuval Peres, Jay Rosen, and Ofer Zeitouni.



1  Introduction

Let (Xn) be a simple random walk on Z2 and Tn(x)=åj=1n 1{Xj=x} be the number of visits to x before time n. Let Tn*=maxxÎZ2Tn(x) be the number of visits to the most visited point. The Erdös--Taylor conjecture asserts that
 
lim
n®¥
Tn*
(log n)2
=
1
p
,   almost surely.     (1)
Erdös and Taylor [7] proved the upper bound 1/p and a lower bound 1/(4p). The main result of the talk is that the Erdös--Taylor conjecture is true.

Let (Xj~) be a simple random walk on the two-dimensional torus Zn2=Z2/nZ2. Consider T(x)=min{ j³ 0|Xj~=x }, the time to attain the point x for the first time and
T n=
 
max
xÎZn2
T(x),
the covering time of the torus. The Aldous-Lawler conjecture asserts than
 
lim
n®¥
Tn
(nlogn)2
=
4
p
,  in probability.     (2)
Kesten, Révész, Lawler, and Aldous proved an upper bound 4/p (see [1, Corollary 25, Chapter 7]) and a lower bound 2/p. A related question is the Kesten--Révész conjecture for the simple random walk on Z2 (see [4]).

The proofs for the upper bounds rely on the second moment method, the approximation of random walks by Brownian motions, and an underlying tree structure for the occupation of small disks by a Brownian motion. We give here a sketch of the proofs; see [4, 5] for complete proofs.

2  The Second Moment Method

Janson gives a short account of the second moment method in [2]. Basically, we consider a sequence of non-negative random variables Xn, and we want to estimate P(Xn>0). The second moment method asserts that if
Var(Xn)
(E Xn)2
® 0,     or equivalently,    
E Xn2
(E Xn)2
® 1     (as   n®¥),     (3)
then
P(Xn>0)® 1.     (4)
The method is frequently used in the context of random graphs; for example, this method proves the existence of a Hamilton cycle in random graphs satisfying suitable conditions.

The second moment method is a consequence of the Chebyshev inequality,
P(|X|>t)£
1
t2
E (X2).
As a consequence of the latter,
P(X=0)£ P ( |X-µ|³µ ) £
Var(X)
µ2
,    for µ=E X.

3  Proof of the Erdös--Taylor Conjecture

3.1  Upper bound

By definition, the truncated Green function Gn(x,y) is the expectation of the number of passages at y in n steps, when starting from x.

We have
Gn(0,0)=
n
å
j=0
E ( 1{Xj=0} ) =
n
å
j=0
P(Xj=0)~
logn
p
.
(See Feller [8, p. 361].) Applying [3, Theorem 8.7.3] for the renewal sequence un=P(Xn=0), we deduce that for large n, and fixed small d>0,
P ( Xj¹ 0 for j=1,...,n-1 ) £
(1-d)p
logn
.
This implies by the strong Markov property that
P ( Tn(0)³ ap(logn)2 ) £ æ
ç
ç
è		 1-
(1-d)p
logn
ö
÷
÷
ø		 a(logn)2£ e-ap(logn)(1-d)= n-(1-d)ap.     (5)
We now consider the disk of center zero and radius n(1+d)/2. The probability that the random walk exits this disk before time n tends to zero as n tends to infinity, and the number of points of Z2 inside this disk is close to p n(1+d). From Equation (5), we then get
Pna£P æ
ç
ç
è
 
max
0£ i£ n
|Xi|> n(1+d)/2 ö
÷
÷
ø		 +p n(1+d)n-(1-d)ap,     (6)
where Pna=P(Tn*³ a(logn)2). The first term of the right member of Equation (6) vanishes as n tends to infinity. Therefore, applying the Borel--Cantelli lemma to the subsequence P2ma, for a>1/p, and using interpolation for all n, we have P(limsupTn*³ a p(logn)2))® 0. This gives an upper bound 1/p.

3.2  Lower bound

We can try to adapt the proof from the upper bound and use the second moment method. Let D(x,r) be the disk of center x and radius r and
Zn=
 
å
xÎ D(0,(n)1/2)
1
 
{ Tn(x)³b (logn)2 }
.
Adapting the proof of the upper bound (Equation (6)) gives E Zn » n(1-bp). Therefore,
E Zn2
(E Zn)2
=
1
E (Zn)
+
Sx,y
Sx,y+Sx
,     where      Sx=
 
å
xÎ D(0,(n)1/2)
( P ( Tn(x)³b(log n)2 ) ) 2
and      Sx,y=
 
å
x¹ yÎ D(0,(n)1/2)
P ( Tn(x)³b(log n)2 )  P ( Tn(y)³b(logn)2 ) .
A naive approach would say the following: the number of summand in Sx,y is O(n2(1-bp)) while it is only O(n(1-bp)) in Sx. Therefore, for b<1/p, E Zn2/(E Zn)2® 1 and P(Tn*³1/p(logn)2)=1 almost surely. However, Erdös and Taylor [7] show that the correlation structure between points x such that P(Tn(x)³b(log n)2) is too strong to get this result. They obtain an upper limit 1/(4p). We move in the following section to a tree model to overcome this difficulty.

Modelling by a (toy) tree problem
We1 consider a complete binary tree Bm of height m and a (nearest neighbor) random walk X starting from the left-most leaf a, with probability 1/3 of choosing any direction when being at an internal node. In this model, the starting point a and the root 0 respectively represent the origin (0,0) and the boundary of a ``disk'' of radius m on Z2. Let Lm be the set of leaves of Bm. We consider Tm(x), the time spent at leaf x before hitting the root 0, and
Tm*=
 
max
xÎ Lm
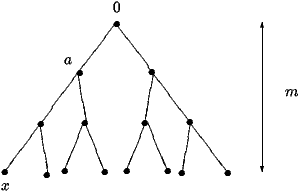
Tm(x),
its maximum over all leaves.

Let us denote by 0, 1, 2,...,a=m the nodes of the ray going from the root 0 to a and let Py denote probability for walks starting from node y. We consider
Hy=Hy(u)=
 
å
u³ 0
Py ( X spends time k at a before hitting 0 )  uk.
For any node i of the ray (0,a), and for any node y of the subtree rooted at the right child of i, the probability of k visits to a before hitting 0 of the walk starting from y is the same as if the walk starts from i; this implies Hy=Hi. This last result is true for all i from 1 to m-1.

We can therefore consider only the nodes of the ray (0,a), which provide the set of equations
H1=
H2
3
+
H1
3
+
1
3
,   Hk=
Hk-1
3
+
Hk
3
+
Hk+1
3
(2£ k £ m-2),   Hm-1=
Hm-2
3
+
(1+u)Hm-1
3
.
Solving yields
Ha(u)=Hm=
1
m
×
1
1- æ
ç
ç
è		 1-
1
m
ö
÷
÷
ø		 u
,   and   H1(u)=
m-1-(m-2)u
m-(m-1)u
.     (7)
The random variable Tm(a) therefore has a geometric distribution with mean m-1, which induces (for large m)
P ( Tm(a)>a m2 ) = æ
ç
ç
è		 æ
ç
ç
è		 1-
1
m
ö
÷
÷
ø		 m ö
÷
÷
ø		 a m~ e-a m  and  P(Tm*>a m2)£ e-a m 2m=e-(a-log2)m.
This implies the same upper bound as precedently (up to the change of model).

We now consider a variation of the second moment method. We fix some K large. We denote by x-ray the ray from the root 0 to a leaf x and Ni(x) counts the number of excursions from level i to level i+1 on the ray x. We define the x-ray as a-successfull if
Ni(x)~ a i2,    for    i=0, K, 2K, ...,K ê
ê
ê
ë
m
K
ú
ú
ú
û		 .
We have
P (  Ni+K(x)~a(i+K)2 | Ni(x)~a i2 ) ~ e-a K  Þ  P(x-ray is a-successfull)~ e-a m.
We now have
P(x-ray and y-ray are a-successfull) ~ e-2a mea r(x,y),
where r(x,y) is the depth of the first common ancestor of x and y. This induces a reduction of variance. Considering now the random variable Zm defined by
Zm=
 
å
xÎ Lm
1{x-ray a-successfull},
we have
E Zm2
(E Zm)2
~
m/K
å
s=1
e(a-log 2)Ks® 1   for   a<log2,
when first m and then K tend to infinity. There is no obvious way to adapt this result to the standard random walk, but it is possible to adapt it to the planar Brownian motion that we denote w=(wt).

Define q as the first time where the Brownian motion w hits the circle of radius 1 and µqw(A) as the occupation time of a subset A of the disc D(0,1) until this time. We have
q=min {  t | |wt|=1  }
and    µqw(A)= ó
õ
q


0
1A(wt)dt.
The Perkins--Taylor conjecture states for the Brownian motion that
 
lim
e® 0
 
sup
|x|<1
µqw(D(x,e))
e2 ( loge ) 2
=2.     (8)
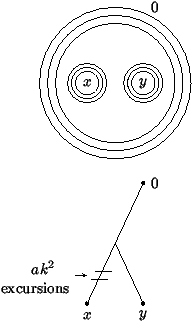We shall in a first time sketch a proof of this conjecture and apply then the KMT approximation theorem of the Brownian motion by the standard random walk.
Sketch of proof for the Perkins--Taylor conjecture
In the following, let D(x,r) be the boundary of the disk D(x,r).

The proof of the upper bound of the conjecture follows the same line as for the standard random walk. When considering the lower bound, the difficulty relies again in the correlation structure.

Let ek=e-k and define a point x of D(0,1) as k-successful if the number of excursions of the Brownian motion between D(x,ek) and D(x,ek+1) is a k2 for fixed a. We remark that if x is successful, the time spent at the ball D(x,ek+1) is a k2e2~ a e2(loge)2, where e=ek+1, with probability close to 1.

KMT approximation theorem
The Komlós--Major--Tusnády (KMT) approximation theorem [9] states that for each n it is possible to construct a random walk {Xk}k=1n and the Brownian motion {wt}0£ t £ 1 on the same probability space so that for any d>0 and any h>0
 
lim
n®¥
P æ
ç
ç
è
 
max
k=1,...,n
½
½
½
½		 wk/n-
(2)1/2
(n)1/2
Sk ½
½
½
½		 > d nh-1/2 ö
÷
÷
ø		 =0.     (9)
(The original one-dimension KMT approximation has been extended to the multivariate case by Einmahl [6]).

Note that the Brownian motion between two successful points x and y before reaching the boundary may again be modelized by a tree structure, and that the same technique as for trees works once more (with many technical issues).

Application of the KMT approximation theorem
The proof follows by considering the lattice points inside the circle {z:|(2)1/2 z -y|<(n)1/2(1+2d )en} whose number is less than
p
2
n(1+2d)3en2.

4  Covering Time of the Torus



First, we once again consider the ``toy'' problem of the covering time of the binary tree Bm. Let X=(Xn) be the first neighbor random walk starting from the left son a of the root, and consider hits to x, the leftmost leaf. Px again refers to walks starting at point x.

4.1  Upper bound

From Section 3.2 we get
Pa(X hits x before 0)=1-H1(0)=
1
m
.
This implies that
P0(X does not cover x during first N visits to 0) ~ æ
ç
ç
è		 1-
1
2m
ö
÷
÷
ø		 N.

Let P0 be the probability that the random walk starting at zero does not cover the binary tree Bm during N visits to 0. We have
P0£2m æ
ç
ç
è		 1-
1
2m
ö
÷
÷
ø		 N    so that     P0® 0     for    N=2(1+d)m2log 2.
The time needed for N visits to the root is 2m+1N; this implies that
P0 ( X does not cover Bm before time 2(1+d)log2× m2 2m+1 ) ® 0.

4.2  Lower bound

A ray x is called successful if the number of excursions from level i to level i+1 in the ray is a(m-i)2. Dembo et al. apply a second moment analysis to the successful rays to show that, with probability one, before 2(1-d)m2log2 visits to the root, there are points which are not covered. Then, the time needed to visit the root that many times is about 2(1-d)m2(log2)2m+1.

To solve the standard random walk problem on Z2, Dembo et al. first solve the equivalent problem for the Brownian motion on the torus T2, where T2 is identified with the set (-1/2,1/2 ]2.

Let T(x,e) denote the time needed by the Brownian motion to enter the ball D(x,e),
T(x,e)=inf {  t>0 | wtÎ D(x,e)  } ,  and    Ce=
 
sup
xÎ T2
T(x,e).
Therefore, Ce is the minimum time needed for the Brownian motion Wt to come within e of each point of T2. Equivalently, Ce is the amount of time needed for the Wiener sausage of radius e to completely cover T2. Dembo et al. [4] prove that
 
lim
e ® 0
Ce
(log e)2
=
2
p
,     almost surely.
Using the KMP strong approximation theorem again provides the result for the standard random walk on T2.

References

[1]
Aldous (D.) and Fill (J.). -- Reversible Markov chains and random walks on graphs. -- Monograph in preparation.

[2]
Aldous (David) and Pemantle (Robin) (editors). -- Random discrete structures. -- Springer-Verlag, New York, 1996, xviii+225p. Papers from the workshop held in Minneapolis, Minnesota, November 15--19, 1993.

[3]
Bingham (N. H.), Goldie (C. M.), and Teugels (J. L.). -- Regular variation. -- Cambridge University Press, Cambridge, 1987, xx+491p.

[4]
Dembo (Amir), Peres (Yuval), Rosen (Jay), and Zeitouni (Ofer). -- Cover times for Brownian motion and random walks in two dimensions. -- To appear.

[5]
Dembo (Amir), Peres (Yuval), Rosen (Jay), and Zeitouni (Ofer). -- Thick points for planar Brownian motion and the Erdös-Taylor conjecture on random walk. Acta Mathematica, vol. 186, n°2, 2001, pp. 239--270.

[6]
Einmahl (Uwe). -- Extensions of results of Komlós, Major, and Tusnády to the multivariate case. Journal of Multivariate Analysis, vol. 28, n°1, 1989, pp. 20--68.

[7]
Erdös (P.) and Taylor (S. J.). -- Some problems concerning the structure of random walk paths. Acta Mathematica Academiae Scientiarum Hungaricae, vol. 11, 1960, pp. 137--162. (Unbound insert).

[8]
Feller (W.). -- An introduction to probability theory and its applications. -- Wiley international edition, 1970. Volume 1.

[9]
Komlós (J.), Major (P.), and Tusnády (G.). -- An approximation of partial sums of independent rv's and the sample df. I. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, vol. 32, 1975, pp. 111--131.
1
The elementary proof leading to Equation (7) was not presented by the speaker and is due to the authors of the summary.
This document was translated from LATEX by HEVEA.