Asymptotics for Random Combinatorial Structures

Asymptotics for Random Combinatorial Structures

Amir Dembo

Mathematics and Statistics Department, Stanford University (USA)

Algorithms Seminar

June 18, 2001

[summary by Philippe Flajolet]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract

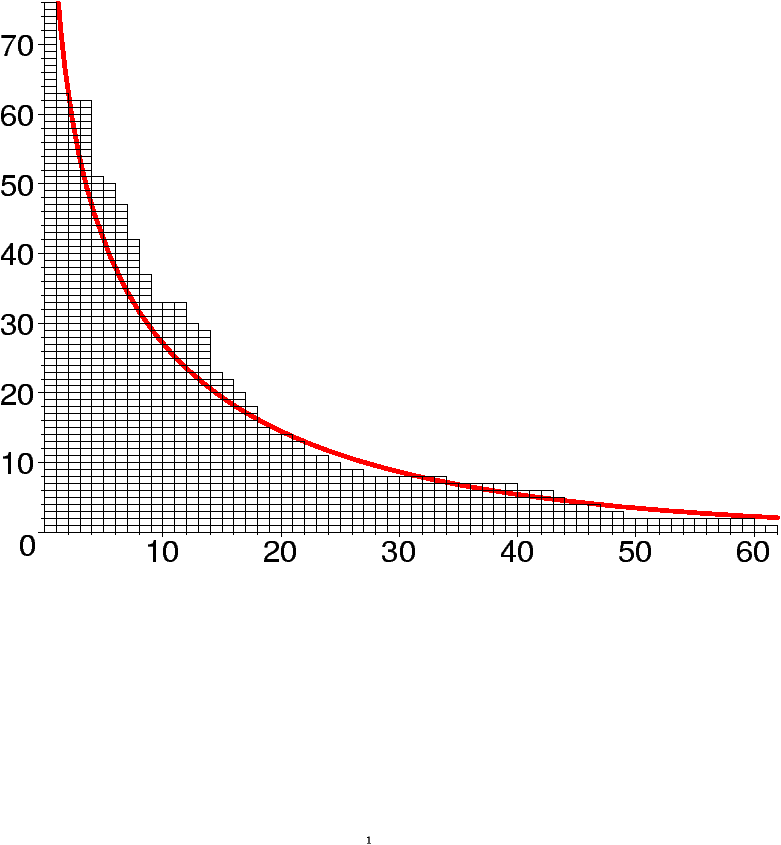
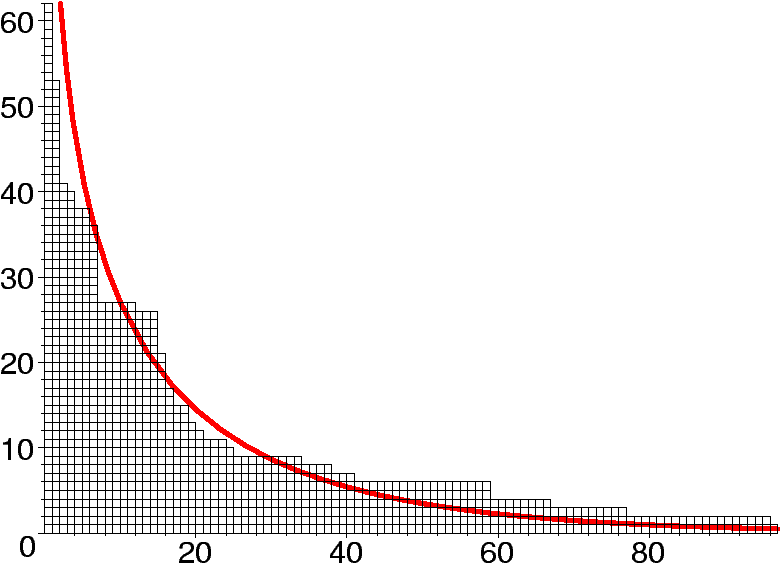
What does a random partition of a large integer look like? The talk presents asymptotic results and variational problems for this question, obtained in a work of A. Dembo jointly with A. Vershik and O. Zeitouni [4]. The techniques involve some combinatorics and mostly probability theory. Other applications concern asymptotics of various random combinatorial structures, such as permutations, forests of trees, and convex polygons with integer vertices. This summary is intended as a casual introduction to the reading of the paper [4].

1 A Bit of Paleontology

A partition of the integer n is an aditive decomposition of the integer n into some number r of integer summands,

n=x₁+x₂+···+x_r, x_j³ x_j+1, x_r>0.

The quantity r is called the number of summands (or parts). A partition is said to be strict if all its summands are distinct. A partition is naturally represented by a diagram resembling a staircase and called diversely its Ferrers graph or its Young diagram. We shall let P_n and P_n^s denote the collections of all partitions and strict partitions summing to n, and denote with P_n, P_n^s the corresponding cardinalities.

Euler started the analytic theory of partitions by providing the explicit generating functions

P(z)=

P_nzⁿ =

k³1

1-z^k

, P^s(z)=

P_nzⁿ=

k³1

(

1+z^k

)

and a good deal more. The next century mostly focussed on the corresponding theta function identities and their elliptic-modular aspects. Andrews' classic [2] is still a pretty good reference for many of these aspects.

The asymptotic theory starts 150 years after Euler, with the first letters of Ramanujan to Hardy in 1913; see [7]. There, Ramanujan stated:

The coefficient of xⁿ in (1-2x+2x⁴-2x⁹+···)^-1 is the integer nearest to

1

4n
æ
ç
ç
è coshp(n)^1/2-

sinh p(n)^1/2

p(n)^1/2
ö
÷
÷
ø .

This assertion (that in fact needs to be mildly amended) is, in view of Euler's pentagonal number theorem, directly relevant to our subject. In a celebrated series of memoirs published in 1917 and 1918, Hardy and Ramanujan found very precise estimates for the partition numbers implying in particular:

P_n~

4n(3)^1/2

n)^1/2

, P_n^s~

4(3)^1/2n^3/4

n)^1/2

. (1)

See [7, Ch VIII] for an insightful discussion and [2, Ch. 5] for the reexamination of the subject by Meinardus.

As far as dominant asymptotics goes, it may be worth pointing out that the simply stated estimates (1) plainly derive from a saddle-point approximation of the Cauchy coefficient integral,

[zⁿ] C(z)=

2ip

ó
õ

|z|=z

C(z)

zⁿ⁺¹

. (2)

The saddle points to be used here are at the real points z (for P(z)) and z^s (for P^s(z)) such that

z~ 1-

(6n)^1/2

, z^s~ 1-

(12n)^1/2

the reason being that P(z) and P^s(z)=P(z)/P(z²) tend to infinity like exp(p²/6(1-z)) and exp(p²/12(1-z)), as z tends radially to 1.

Later in the last century, Erdös and Lehner [6] launched the study of various characteristics of random partitions. In particular, they showed that almost all partitions of P_n have a number a summands in an interval

(n)^1/2logn± o

(

(n)^1/2logn

)

, C:=p(

)^1/2, (3)

while for strict partitions, the interval is

2(n)^1/2

log2± o

(

(n)^1/2

)

, D:=p(

)^1/2. (4)

The limit law is an extreme value distribution in the first case, a Gaussian distribution in the second case. (Erdös and Lehner use a mostly elementary recurrence argument induced by generating functions together with the Hardy--Ramanujan estimates.) Note the similarities between the saddle-point constants and the normalization constants C, D in (3) and (4). Also, the scaling factor (n)^1/2 is ubiquitous in all such analyses. Roughly put, these estimates inform us that a random partition of n is expected to fit in a rectangle with sides about n^1/2+o(1).

2 The Shape of Random Partitions

Around 1977, Vershik and Kerov [10] and, independently, Logan and Shepp [8] studied the shape of the Young tableau(s) associated to a random permutation or a random involution.¹ Thus, in contast to what happens in the talk, we are momentarily dealing with a non-uniform distribution on P_n. Indeed, the enumerative formulae relative to Young tableaus under these statistics (the ``hook formula,'' also called the Robinson--Frame--Thrall formula) renormalize in the scale of (n)^1/2 in such a way that the probability of a continuous shape f(t) (in the asymptotic limit) occuring in tableaus of size n is found to be of the rough form (see (7) below for a precise statement)

e^{-n Q(f)}, Q(f):=2

ó
õó
õ

t<s

log

(

2e^1/2(s-t)

)

æ
ç
ç
è

(s)

ö
÷
÷
ø

æ
ç
ç
è

(t)

ö
÷
÷
ø

dt ds (5)

with f^. the derivative of f. Thus, the most likely shape f₀ solves the variational problem of minimizing the functional Q, and ``most'' tableaus are expected to be close to this particular shape f₀. From the methodological standpoint, the contributions [8, 10] are especially important. They led to a much wanted solution of Golomb's conjecture to the effect that the average length of the longest increasing subsequence in a random permutation of size n is asymptotic to 2(n)^1/2; see [1, 3] for recent developments in rather different directions.

Figure 1: Two partitions of P₁₀₀₀ drawn at random against the limiting shape Y(t).

We now return to partitions and let Q_n and Q_n^s represent the uniform probability models on P_n and P_n^s. A partition (or diagram) l can be written under the form l=1^r₁2^r₂3^r₃···. Graphically, we define the ``contour'' or ``shape,''

j_l(t):=

k=é tù

r_k, t³0,

so that j_l is a monotone decreasing function whose integral over R⁺ equals n. We normalize any such j by

(t)=

(n)^1/2

j_l

(

\lceil

t(n)^1/2

\rceil

)

Under the models induced by Q_n and Q_n^s, Vershik [9] proved (in the sense of uniform convergence on compact sets) that contours tend to converge to deterministic limits,

(·

)

¾®

n®¥

Y(·

^s(·

)

¾®

n®¥

Y^s(·), where

Y(t):=

ó
õ

e^{a u}-1

du, Y^s(t):=

ó
õ

e^{b u}+1

du, a=

(6)^1/2

, b=

(12)^1/2

. (6)

Thus, a random partition under Q_n or Q_n^s tends to have a limiting shape given by the curves Y(t) or Y^s; see Fig. 1 obtained with Maple and combstruct. (Observe that Y has a logarithmic singularity at 0, while Y^s is regular there.) Alternatively, the limit contours are the curves satisfying respectively e^-a
x+e^{-a y}=1, and e^{b y}-e^{-b y}=1, with the first one being symmetrical, as it should.

The main objective of the talk is to consider deviations from the limit shapes. What is proved is a full large deviation principle, of speed (n)^1/2, much in the spirit of (5). We recall that a sequence of measures µ_n over a (completely regular Hausdorff topological) space X is said to satisfy the large deviation principle [LDP] with speed b_n and a rate function I if I : X®[ 0,¥) is lower semicontinuous, and for any measurable set XÌX, there holds:

-inf

_{xÎ X^°}I(x) £

liminf

n®¥

b_n

log

µ_n(X)£

limsup

n®¥

b_n

logµ_n(X)£ -inf_{xÎ X}I(x). (7)

There, X^° and X denote the interior and the closure of X. It can be recognized that the informally stated estimate in (5) is of this type (with speed b_n=n and rate function Q).

For our purposes, the set X will consist of functions that are left continuous and of right limits equipped with the topology of uniform convergence. Let also AC_¥^[ -1,0 ] be the subset of non-increasing absolutely continuous functions f(·) satisfying lim_t®¥f(t)=0---and hence f(t)=ò_t^¥(-f^.(u)) du---with derivatives belonging Lebesgue-almost everywhere to the interval [ -1,0 ]. This last set represents the collection of all potential ``shapes'' of partitions considered (after normalization). By want of space, we refer to the original paper [4] for complete topological and measure-theoretic definitions and state:

Theorem 1 Under the laws Q_n^s, the random variable j^~(·) satisfies the LDP with speed (n)^1/2 and a rate function that, for fÎAC_¥^[ -1,0 ] and ò₀^¥(-t) df(t)£1, is expressed by

I^s(f)=2b-

ó
õ

æ
ç
ç
è

(t)

ö
÷
÷
ø

dt,

with h(x)=log(x^-x(1-x)^-(1-x)) the entropy function and g_ac the absolutely continuous part of g.

Theorem 2 Under the laws Q_n, the random variable j^~(·) satisfies the LDP with speed (n)^1/2 and a rate function that, for f in a suitable space and ò₀^¥(-t) df(t)£1, is expressed by

I^s(f)=2a-

ó
õ

æ
ç
ç
è

(t)

ö
÷
÷
ø

æ
ç
ç
ç
ç
ç
è

(t)

ö
÷
÷
÷
÷
÷
ø

dt.

The paper also states some equivalent forms that are expressed in terms of a ``distance'' to the most likely contours of (6). That distance involves various entropy functions.

3 Boltzmann Models of Combinatorics

The first step in the proof of Theorems 1 and 2 is the introduction of a family of models over the classes P and P^s and large deviations are first established under these models. Since the principles are of an applicablity that goes well beyond the probabilistic theory of partitions, we depart a bit from the original paper [4] and discuss them first at a fair level of generality.

Let generally C be a class of combinatorial objects endowed with its size function |·|. What we call here, by virtue of a vague analogy with statistical mechanics, the Boltzmann model of parameter x (over C) is the model that assigns to any object gÎC the probability

x^|g|

C(x)

with

C(x)=

gÎ C

x^|g|,

the counting generating function of C. There x is to be restricted to real values less than the radius r of convergence of C(x).

The class C being fixed, we shall let Q_n denote the uniform probability model over the subclass C_n of objects of size n and, with a slight abuse of notations, Q_x represents the Boltzmann model of parameter x. Clearly, Q_x is a mixture of the family of models {Q_n} in the following sense:

Q_x @ Q_N where N is a random integer selected with P(N=n)=

C_nxⁿ

C(x)

. (8)

In other words, a randomly chosen object under Q_x has a random size Nº N_x distributed according to the probability in (8); once the value of size has been drawn according to its distribution, say, N=n, a random element of C_n is chosen uniformly at random, that is, according to Q_n. (Accordingly, Q_n is Q_x conditioned upon size, irrespective of the value of xÎ(0,r).) The distribution of the random size N according to Q_x is itself given by a simple generic calculation that we now explain. The probability generating function of N is

P(N=n) zⁿ=

C(xz)

C(x)

Next, the mean and second moment of N are found to be

E(N)=x

C'(x)

C(x)

, E(N²)=

x²C''(x)+xC'(x)

C(x)

. (9)

The mean size increases as x approaches r^-, with r the radius of convergence of C. In particular, if the additional condition C'(r^-)=+¥ is met, the Boltzmann model must give preponderance to objects of larger and larger sizes. (Work in progress by Duchon, Flajolet, Louchard, and Schaeffer shows that similar considerations are otherwise of great interest for the random generation of combinatorial structures.)

We now specialize the Boltzmann model to partitions, with the Boltzmann models Q_x, Q_x^s, and the fixed-size models Q_n, Q_n^s taken in association to the combinatorial classes P, P_n^s. The generating functions P(z), P^s(z) have radius of convergence r=1 and both blow up exponentially as z®1^-. Thus, the models Q_x, Q_x^s must have something to say on the limiting behaviours of objects in P, P_n^s. As it is easy to see, the Boltzmann models Q_x and Q_x^s correspond to infinite sequences of independent integer valued random variables R_k (k=1,2,...), with laws as follows:

Q_x :		R_kÎZ_>0,	P(R_k=l)=x^kl(1-x^k)
Q_x^s :		R_kÎ {0,1},	P(R_k=1)=x^k/(1+x^k).

(10)

In other words, the non-indentically distributed (but independent) R_k are Bernoulli in the case of Q_x^s and geometric in the case of Q_x.

A simple calculation based on Equation (9), on Chebyshev's inequalities, and on the usual approximation techniques for partition functions shows that a window narrowly centred around size N=n is obtained by fixing x=x_n, x=x_n^s given by

x_n=1-

(n)^1/2

, x_n^s=1-

(n)^1/2

for Q_x and Q_x^s, respectively. (Note that these values coincide with the saddle points of the complex-analytic approach in Section 1! This fact is general since the equations E_x(N)=n and the saddle-point condition for (2) precisely coincide.) Large deviations of sums of Bernoulli or geometric random variables involve the entropy function. The Boltzmann models for partitions then provide a first hint as to the natural occurrence of entropy functions in the statements of Theorems 1 and 2.

4 The Spirit of Complete Proofs

In this short abstract, we cannot do more than presenting a broad (and vague) outline of what the full proof of Theorems 1 and 2 requires.

First, under the continuous-parameter models Q_x,Q_x^s, it is easy to determine information on single parameters of partitions. The paper under review recovers for instance the analogues of Erdös and Lehner's estimates when x=x_n and x=x_n^s. It then proceeds by proving the LDP for these models. What is required is showing that, for any fixed m, and any fixed ``instants'' t₁, t₂, ..., t_m, the random vectors (j_n^~(t₁),...,j_n^~(t_m),n^-1N) satisfy a large deviation principle. The proof bases itself on the independence granted by the models: one needs to estimate the probabilities of ``slices'' of summands in the scale of (n)^1/2 to be away from what is expected; this is largely based on the approximation of Riemann sums by integrals. As a snapshot of the latter technique, we offer the simple estimate

E_{x_n}

æ
ç
ç
è

(t)

ö
÷
÷
ø

k=tn^1/2

(n)^1/2

x_n^k

1-x_n^k

ó
õ

e^{a u}-1

du =:Y(t).

Last but not least, the treatment relies on an intensive use of large deviation techniques as exposed in [5].

In a second step, a Tauberian type of process needs to be applied. Indeed, the models Q_{x_n} are a sort of weighted average of various models of a size N, which is only controlled to lie in the vicinity of n but still fluctuates randomly. However, results at N=n exactly are wanted. Contour integration is one common way of achieving this, but the authors of [4] opt for a more combinatorial path. One of the ideas is to appeal to the following area transformation: given a diagram l of area N at most n, form a new diagram of area n exactly, by completing the last row of l by n-N elements. This establishes a mapping from È_N=1ⁿP_N to P_n that does not affect shape and various other characteristics of partitions too much. In this way, large deviation properties established for values of N slightly smaller than n (as given by the family of Q_{x_n} models) can be ``transferred'' to partitions of exact size n, that is, to the model Q_n.

The paper under discussion concludes by noting that several such large deviation principles should hold for various types of partitions with multiplicities and constrained partitions, as well as labelled trees and set partitions. In the last case, the objects at stake are enumerated by exponential generating functions, and suitable adaptations of the Boltzmann models (with the Poisson distribution replacing the geometric or Bernoulli distribution) are lurking in the background.

References

[1]: Aldous (David) and Diaconis (Persi). -- Longest increasing subsequences: from patience sorting to the Baik-Deift-Johansson theorem. Bulletin of the American Mathematical Society (New Series), vol. 36, n°4, 1999, pp. 413--432.
[2]: Andrews (George E.). -- The theory of partitions. -- Addison-Wesley Publishing Co., Reading, Mass.-London-Amsterdam, 1976, xiv+255p. Encyclopedia of Mathematics and its Applications, Vol. 2.
[3]: Baik (Jinho), Deift (Percy), and Johansson (Kurt). -- On the distribution of the length of the longest increasing subsequence of random permutations. Journal of the American Mathematical Society, vol. 12, n°4, 1999, pp. 1119--1178.
[4]: Dembo (A.), Vershik (A.), and Zeitouni (O.). -- Large deviations for integer partitions. Markov Processes and Related Fields, vol. 6, n°2, 2000, pp. 147--179.
[5]: Dembo (Amir) and Zeitouni (Ofer). -- Large deviations techniques and applications. -- Jones and Bartlett Publishers, Boston, MA, 1993, xiv+346p.
[6]: Erdös (Paul) and Lehner (Joseph). -- The distribution of the number of summands in the partitions of a positive integer. Duke Mathematical Journal, vol. 8, 1941, pp. 335--345.
[7]: Hardy (G. H.). -- Ramanujan: Twelve Lectures on Subjects Suggested by his Life and Work. -- Chelsea Publishing Company, New-York, 1978, third edition. Reprinted and Corrected from the First Edition, Cambridge, 1940.
[8]: Logan (B. F.) and Shepp (L. A.). -- A variational problem for random Young tableaux. Advances in Mathematics, vol. 26, n°2, 1977, pp. 206--222.
[9]: Vershik (A. M.). -- Statistical mechanics of combinatorial partitions, and their limit configurations. Funktsional'nyi Analiz i ego Prilozheniya, vol. 30, n°2, 1996, pp. 19--39, 96.
[10]: Vershik (A. M.) and Kerov (S. V.). -- Asymptotics of the Plancherel measure of the symmetric group and the limiting form of Young tables. Soviet Mathematics Doklady, vol. 18, 1977, pp. 527--531.

1: These are ``filled'' Young diagrams---the filling rule corresponds to entries increasing by line and column.

This document was translated from L^AT_EX by H^EV^EA.