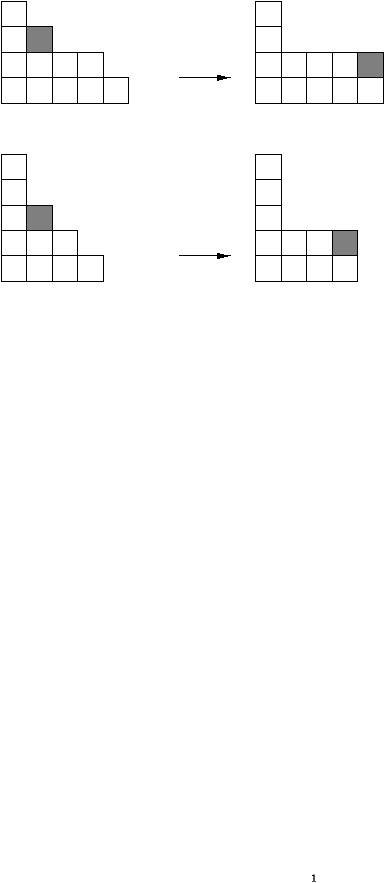
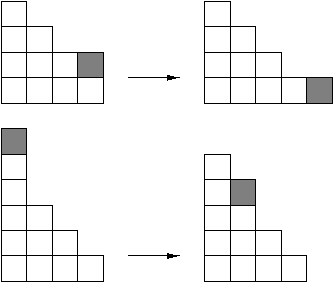
(a)(b)
Figure 1: (a) Application of horizontal rule
to (5,4,2,1) and (4,3,2,1,1); (b) application of vertical rule to
(4,4,2,1) and (4,3,2,1,1,1).
Sand piles are integer partitions that can be obtained from a column of n grains by moving grains from left to right according to rules defined by a model. We try to better understand the structure of those objects by decomposing and counting them. For the model introduced by Goles, Morvan, and Phan, we fing generating functions according to area, height, and width. We establish a bound for the number of the sand piles consisting of n grains in IPM(k) for large n. We present the series according to area and height for Phan's model L(q). We introduce a more general model, where grains can also go to the left, that we call Frobenius sand piles. (Joint work of S. Corteel with D. Gouyou-Beauchamps (LRI, Orsay)).
| ( | p'1,···,p'p1 | ) | is replaced with | ( | p'1,···,p'i-1,p'i+1+1,···,p'p1 | ) | . |
| ( | p'1,···,p'p1 | ) | is replaced with | ( | p'1,···,p'i-1, p'i+1,···,p'j, p'j+1+1,···,p'p1 | ) | . |
In the SPM(k) model (Sand Pile Model), introduced by Goles and Kiwi [3], the initial configuration is made of one column of n grains, and the only available rule is the vertical rule.
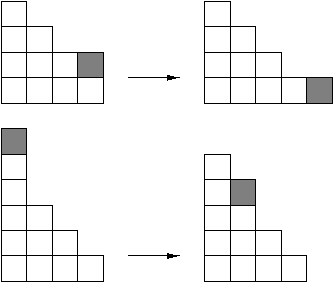 (a)(b)
(a)(b)
Figure 1: (a) Application of horizontal rule to (5,4,2,1) and (4,3,2,1,1); (b) application of vertical rule to (4,4,2,1) and (4,3,2,1,1,1).
|
|||||||||||||
|
|
|
= |
|
|
= |
|
( | 1+qi | ) | . |
In Figure 2, the maximal element (1,1,1,1,1,1) is on the left.
| l+1 |
| 3 |
| Sk(q,x)=1+ |
|
xl(p)q|p| =1+ |
|
|
Sk(q,xqi) +xqk+1Sk(q,xqk). |
Proof. A sand pile in IPM(k) is either the empty partition, or a partition in IPM(k) where one duplicates i times the highest column and adds to it at least one part i (1£ i£ k), or a partition in IPM(k) where one duplicates k times the highest column and adds to it one part of length k+1. This decomposition yields the last expression for Sk(q,x) in the statement of the theorem, after noting that Sk(q,xqr) is the generating function obtained by duplicating r times the highest column in each sand pile.
Figure 3: Decomposition of a sand pile in IPM(1).
| S1(q,x)=1+ |
|
xnqn(n+1)/2 |
|
æ ç ç è |
q+ |
|
ö ÷ ÷ ø |
; S¥(q,x)= |
|
æ ç ç è |
q+ |
|
ö ÷ ÷ ø |
. |
| Sk(q,y)= |
æ ç ç è |
|
+ykqk-1 |
ö ÷ ÷ ø |
Sk(q,yq)+ykqk-1 | ( | Sk(q,yq)-Sk(q,yq2) | ) | . |
| S | 1(q,y)=1+ |
|
ynqn(n-1)/2 |
|
|
. |
|
||||||||||||||||||||
|
| Pk(x,y)= |
|
. |
| Pk(x)= |
|
. |
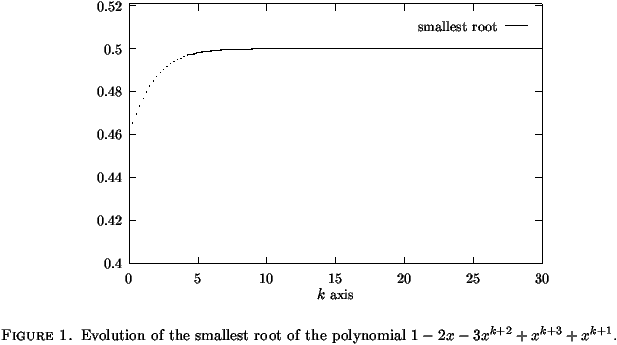
| pk=[qn] |
|
|
, Bk=( |
|
)1/2, and Ck= |
|
æ ç ç è |
|
ö ÷ ÷ ø |
1/4. |
| Lq(q,x)= |
|
+ |
æ ç ç è |
|
+xq-1qq |
ö ÷ ÷ ø |
Lq(q,xq). |
| L | q(q,x)= |
|
xq nqq n(n+1)/2 |
|
|
æ ç ç è |
q+ |
|
ö ÷ ÷ ø |
. |
|
al³ |
|
bl. |
| l+1 |
| 3 |
|
| 1+ |
|
qk |
|
|
. |
| Fk(n)=[qn] |
æ ç ç è |
1+ |
|
qj |
|
|
ö ÷ ÷ ø |
. |
|
xnqn(n+1)/2 |
|
æ ç ç è |
q+ |
|
ö ÷ ÷ ø |
. |
This document was translated from LATEX by HEVEA.