Aléa discret et mouvement brownien*
Philippe Chassaing
Institut Élie Cartan, Université Nancy 1 (France)
Algorithms Seminar
March 26 and 27, 2001
[summary by Philippe Chassaing]
A properly typeset version of this document is available in
postscript and in
pdf.
If some fonts do not look right on your screen, this might be
fixed by configuring your browser (see the documentation here).
Les liens entre le mouvement brownien et ses processus dérivés
(méandre, pont, excursion) d'une part et d'autre part des objets
combinatoires comme les mots de Dyck, les permutations bi-ordonnées,
le tri Shell's sort, les arbres simples, les facteurs gauches,
le hachage ou parking, les animaux dirigés, le graphe aléatoire, la
marche aléatoire dans le plan fendu, ..., rendent opportune une
revue (forcément partielle) des innombrables propriétés du mouvement
brownien.
En combinatoire et analyse d'algorithmes, beaucoup d'asymptotiques de
statistiques intéressantes sont familières aux spécialistes du
mouvement brownien : la hauteur ou la largeur des arbres simples
normalisées convergent en loi vers une loi liée à la fonction q
de Jacobi, connue pour être la loi du maximum de l'excursion
brownienne. Dans l'asymptotique des nombres de Wright, dénombrant les
graphes connexes à n sommets et k arètes en
excès [19], apparaissent les moments de la surface sous
l'excursion brownienne, dont la distribution s'exprime à l'aide de la
fonction d'Airy1. Le
profil moyen d'un arbre simple suit asymptotiquement la loi de
Rayleigh, qui est la loi du maximum du pont brownien. Le déplacement
total dans une table de hachage pleine, est également asymptotiquement
distribuée selon une loi d'Airy. Il est tentant de voir ces faits
comme les fragments d'un même tableau : la convergence des chemins de
Bernoulli (resp. de Dyck) et d'objets analogues vers le mouvement
brownien (resp. l'excursion brownienne). Une version arbre en est
donnée par Aldous avec sa convergence des arbres simples vers le
continuum random tree.
À cette premiere explication de l'omniprésence de certaines lois vient
s'ajouter le principe d'invariance
[7]2 selon
lequel la loi limite de différentes fonctionelles d'une marche
aléatoire ne dépend que très peu (à un facteur multiplicatif près) de
la loi d'un pas élémentaire : ce dernier principe se traduit, par
exemple, en informatique fondamentale, par l'apparition de la même loi
limite pour la hauteur de différents arbres
simples [8, 16], ou encore de la meme loi limite pour le
cheminement total d'un arbre binaire ou pour le déplacement total
d'une table de hachage pleine.
Pour beaucoup d'autres situations combinatoires (tailles de
composantes connexes du graphes aléatoires, minimum spanning
tree, random mappings, cartes planaires, etc.), l'existence
d'un objet aléatoire limite est soupçonnée ou avérée, expliquant ainsi
les lois limites déjà observées, fournissant éventuellement de
nouveaux résultats asymptotiques en combinatoire et en analyse
d'algorithmes, et posant de nouvelles questions sur l'omniprésent
mouvement brownien. Il est sage pour un mini-cours de se limiter à la
convergence d'objets combinatoires très basiques : chemins de Dyck
(bilatères ou non) et facteurs gauches, tous étant plus généralement
des chemins de Bernoulli, vers le mouvement brownien et ses avatars,
excursion brownienne, méandre et pont. Le mouvement brownien, ses
propriétés, et le théorème de Donsker requièrent une trentaine
d'heures de cours pour un traitement rigoureux ; j'éviterai donc les
démonstrations, et renverrai largement à la bibliographie abondante
sur le sujet, en particulier à [17, 2, 12].
Plan
-
Différents types de chemins aléatoires
- Changement d'échelle brownien (Brownian scaling) et
convergence faible
- Convergence faible : définition et premières conséquences
- Convergence faible : critères et autres caractérisations
- Propriétés du mouvement brownien
- Décompositions remarquables des trajectoires du mouvement brownien
- Diverses propriétés de l'excursion brownienne normalisée,
du pont et du méandre brownien
- Conclusion
Les sections 6 à 8 seront rédigées dans un document ultérieur.
1 Différents types de chemins aléatoires
Definition 1 [Chemins de Bernoulli]
Un chemin de Bernoulli est un chemin sur le réseau engendré
par NE=(1,1) et SE=(1,-1), partant de (0,0), admettant comme
pas élémentaires précisément les pas NE et SE. Il y a 2n chemins
de Bernoulli de longueur n.
Definition 2 [Chemins de Dyck]
Un chemin de Dyck
de longueur 2n est un chemin de Bernoulli
de longueur 2n qui se termine au point (2n,0) et reste positif ou
nul sur toute sa longueur. Il y a
chemins de Dyck de longueur 2n. Un mot de Dyck est la description
d'un chemin de Dyck par la suite de ses pas, i. e.
un mot formé
d'autant de caractères `M' (pour
<< montées >>) que de caractères `D' (pour << descentes >>), et
dont n'importe quel préfixe contient au moins autant de `M' que
de `D'. Il y a une bijection privilégiée (entre mots et chemins),
alors notons indifféremment B2nÅ l'ensemble des
Cn chemins de Dyck de longueur 2n ou l'ensemble des Cn mots de
Dyck de longueur 2n.

( ) Un chemin de Bernoulli
de longueur
n=60 ;
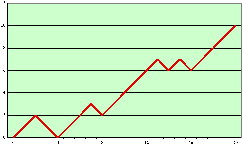
(+) Un facteur gauche de longueur
n=20 ;
(
o) Un chemin de Dyck bilatère
de longueur 2
n=20 ;
(
Å) Le chemin de Dyck de longueur 2
n=20
associé au mot de Dyck
MMMMDDMDMDMMDDMDDMDD.
Figure 1: Différents types de chemins.
Definition 3 [Chemins de Dyck bilatères]
Un chemin de Dyck bilatère
de longueur 2n est un chemin de
Bernoulli de longueur 2n qui se termine au point (2n,0). Il y a
() chemins de Dyck bilatères de longueur 2n.
Definition 4 [Facteurs gauches]
Un facteur gauche
de longueur n est un chemin de Bernoulli
de longueur n qui reste positif ou nul tout au long de sa
trajectoire. Il y a () facteurs
gauches de longueur n.
Variables aléatoires correspondantes
Quitte à identifier une fonction et son graphe, on peut voir
l'ensemble Bn des chemins de Bernoulli de longueur n et ses
sous ensembles BnÅ (ensemble des chemins de
Dyck3), Bno (ensemble des chemins de Dyck
bilatères) et Bn+ (ensemble des facteurs gauches) comme des
parties finies de l'espace C[ 0,n ] des fonctions continues. On
notera nn (resp. nnÅ, nno, nn+) la
mesure de probabilité sur C[ 0,n ] uniforme sur Bn (resp.
BnÅ, Bno, Bn+).
Definition 5
Dans la suite, une variable aléatoire de loi nn (resp.
nnÅ, nno, nn+) sera appelée
marche aléatoire simple symétrique (resp. excursion
de Bernoulli, pont de Bernoulli,
méandre de Bernoulli) de longueur n.
Une variable aléatoire X à valeur dans un espace de fonctions,
p. e. dans C[ 0,1 ], C[ 0,n ] ou encore C[ 0,+¥), est
souvent appelée processus stochastique.
Seule l'appellation << marche aléatoire simple symétrique >> est
bien établie, les 3 autres étant inspirées d'un vocabulaire bien
établi dans le cadre du mouvement brownien, où l'on parle
d'excursion brownienne, de pont brownien, et de
méandre brownien. Dans la suite, par un abus de langage sur
lequel on ne s'attardera pas, on identifiera couramment une suite
u=(uk)0£ k£ n à son prolongement en une fonction f
continue linéaire par morceaux sur [ 0,n ], ou encore au graphe de
cette dernière fonction. En particulier, les fonctions de Bn sont
bien définies par leurs évaluations en 0, 1, 2, ..., n. La
construction usuelle d'une marche aléatoire simple symétrique est
plutôt celle de la suite des n+1 évaluations :
Definition 6 [Marche aléatoire simple symétrique, définition
équivalente]
Notons (Yi)i³ 1
une suite de variables aléatoires
indépendantes et de même loi
(on abrègera << indépendantes et de même loi >> en i. i. d. dans la suite),
avec
P(Yk=1)=P(Yk=-1)=1/2,
et posons
S0=0, Sk = Y1 + Y2+ ...+Yk,
on dit
que S=(Sk)0£ k£ n est la marche aléatoire
simple symétrique
de longueur n.
Remarques
- On verra dans la suite que cette construction révèle certaines
propriétés cruciales des chemins de Bernoulli, dont le mouvement
brownien va hériter par passage à la limite.
- Il est naturel, dans ce contexte, de définir la marche simple
symétrique pour tout entier non négatif, i. e. de
définir un chemin de Bernoulli aléatoire de longueur infinie.
- Plus généralement, une marche aléatoire S=(Sk)k³
0 est définie sur un groupe (G,Å), p. e. ici
(R,+), par
Sk=Y1Å Y2Å ...Å Yk,
les Yi étant i. i. d., la loi de probabilité commune aux Yi étant
appelée << pas >> de la marche. On peut par exemple
associer aux arbres unaires-binaires aléatoires, ou aux arbres
étiquetés aléatoires, une marche aléatoire dont le pas est différent
du pas de la marche aléatoire simple symétrique, i. e. différent de
1/2d-1+1/2d1.
Une fois la marche aléatoire simple symétrique ainsi définie, on peut
voir nnÅ (resp. nn0, nn+) comme
des lois conditionelles de cette marche de longueur n, c'est-à-dire
que, pour AÌC[ 0,n ],
|
|
| nn(A) |
|
|
|
|
|
|
|
|
|
|
|
nnÅ(A) |
| = |
|
=P(SÎ A| Sk³ 0, 0£ k£ n et Sn=0), |
|
|
|
|
|
|
|
|
|
|
|
nn0(A) |
|
|
|
|
|
|
|
|
|
|
|
nn+(A) |
| = |
|
=P(SÎ A| Sk³ 0, 0£ k£ n).
|
|
|
|
|
|
|
|
|
|
|
|
Ces définitions de nn (resp. nnÅ, nn0, nn+)
fournissent un algorithme efficace pour la génération
d'un chemin de Bernoulli aléatoire, et des algorithmes de rejet parfaitement inefficaces
pour la génération des chemins de Dyck (bilatères ou non) ou encore des facteurs gauches.
2 Changement d'échelle brownien (Brownian scaling) et
convergence faible
Definition 7 [Changement d'échelle brownien (Brownian scaling)]
Étant donné une fonction f définie sur un intervalle
[ a,b ] borné, on note f[ a,b ] la fonction définie sur [ 0,1 ] par
| f[ a,b ](t)= |
|
f |
( |
a+t(b-a) |
) |
. |
Le graphe de f[ a,b ] est ainsi obtenu, à partir de celui de
f, en multipliant la largeur par un facteur 1/b-a et la
hauteur par un facteur 1/(b-a)1/2. Bachelier en 1900, ou
Einstein en 1905 (dans leur étude respectivement du cours des actions
en bourse, et du mouvement, observé par Brown en 1826, de certaines
particules en suspension dans un liquide) utilisent explicitement ou
implicitement, une propriété remarquable : le changement
d'échelle brownien d'un chemin de Bernoulli de longueur n converge
vers un objet limite, quand n tend vers +¥.
Notons µn (resp. µnÅ, µno, µn+)
l'image de nn (resp. nnÅ, nno, nn+)
par le changement d'échelle brownien.
Le résultat clé de ce mini-cours est le
Theorème 1
La suite de mesures de probabilités µn (resp.
µnÅ, µno, µn+) sur l'espace C[ 0,1 ]
possède, au sens de la convergence faible, une mesure de probabilité
limite, µ (resp. µÅ, µo, µ+).
La notion de convergence faible est développée Sections 3 et 4. Fixons le vocabulaire.
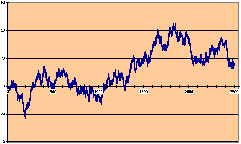
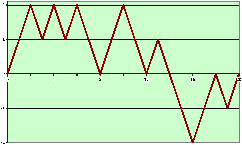
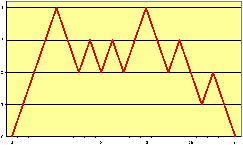
( ) Un chemin de Bernoulli
de longueur
n=2500 ;
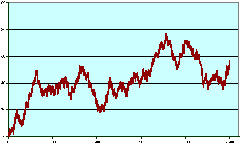
(+) Un méandre de Bernoulli au hasard de
longueur
n=2500 ;

(
o) Un chemin de Dyck bilatère
au hasard de longueur
n=1000 ;
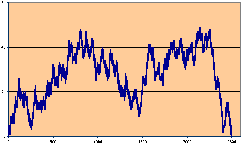
(
Å) Un chemin de Dyck au hasard de
longueur
n=2500.
Figure 2: Chemins de Bernoulli au hasard de
longueur 1000 à 2500 : ils
possèdent en général des fluctuations
d'ordre de grandeur quelques dizaines.
Definition 8 [Mouvement brownien]
La mesure de probabilité µ, définie sur C[ 0,1 ] muni de
sa tribu de boréliens, est appelée mesure de Wiener. Une
variable aléatoire B à valeur dans C[ 0,1 ], ayant pour loi
la mesure de Wiener, est appelée mouvement brownien
(linéaire) (standard).
Definition 9 [Excursion, pont et méandre browniens]
Une variable aléatoire e (resp. b, m) à valeur dans C[ 0,1 ],
ayant pour loi la mesure µÅ (resp. µo, µ+), est
appelée excursion brownienne (normalisée) (resp.
pont brownien, méandre brownien).
Les chemins de Bernoulli de la Figure 2 donnent une idée de l'allure
typique du mouvement brownien ( ), resp. du méandre (+), du pont
(o), de l'excursion brownienne (Å). On peut résumer
les définitions précédentes en un tableau 2×2, suivant la
présence ou l'absence des deux contraintes (de positivité et de retour
en 0 à la fin) :
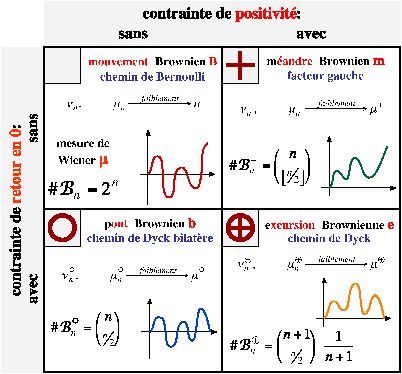
Figure 3: Les différents types de chemins et leurs analogues
browniens.
Remarques
- Le théorème ci-dessus rassemble en fait quatre théorèmes et possède
quatre auteurs : la convergence des marches aléatoires vers la mesure
de Wiener µ, ou vers le mouvement brownien, a été démontrée par
Donsker [6], la convergence vers l'excursion brownienne
par Kaigh [11], la convergence vers le méandre brownien par
Iglehart [9], et celle vers le pont brownien par
Liggett [13].
- Les résultats de Donsker, Iglehart et autres portent en fait sur la
convergence de marches aléatoires, conditionnées ou non, de pas
plus généraux que ceux de la marche aléatoire simple symétrique : les
pas Yi sont toujours i. i. d., mais de loi commune quasiment
quelconque (parfois Yi doit être à valeurs entières, il doit
toujours être centré (E[Yi]=0) et à variance finie
(0<E[Yi2]<+¥)). Cette généralité est bien sûr
intéressante, mais plus particulièrement en combinatoire, ou en
analyse d'algorithme. Par exemple, il est expliqué dans Aldous ou
dans [19] que le mot de Lukasiewicz associé à un arbre
général (resp. étiqueté) de taille n est aussi associé à une marche
aléatoire de longueur n, conditionnée Å, de pas
p=(pk)k³ -1 géomètrique (donné par pk=2-k-2)
(resp. de pas Poisson, donné par pk=1/k+1! e).
Ainsi le résultat de Kaigh permet d'expliquer un faisceau de
comportements asymptotiques de statistiques liées aux arbres
<< généraux >> (resp. aux arbres étiquetés, graphes connexes et,
par exemple, constantes de Wright, hachage linéaire, etc.).
- Une multitude de caractérisations et constructions différentes
du mouvement brownien, du pont, de l'excursion et du méandre brownien,
souvent découlant de propriétés combinatoires des chemins de Dyck ou
de Bernoulli, seront données aux Sections 5 et 7.
3 Convergence faible : définition et premières conséquences
J'abrège encore ici ce qui est expliqué de manière très claire et
assez économique dans le livre fondamental de Billingsley. On se
placera dans un espace métrique (S, S), qui, pour nous, sera
exclusivement Rd ou C[ 0,1 ], muni de la distance usuelle dans
le premier cas, de la distance de la convergence uniforme dans le
second cas ; S désignera la tribu engendrée par (la plus petite
tribu contenant les) ouverts de la topologie induite. Les mesures
considérées seront des mesures de probabilité sur S. Les
résultats ci-dessous s'appliquent à des espaces métriques plus
généraux, dont on exige parfois qu'il soient complets et séparables
(voir [2, 14]).
Definition 10 [Convergence faible]
On dit que la suite de mesures de probabilité (µn)n³ 0
converge faiblement
vers la mesure de probabilité µ, si
et seulement si, pour toute fonction continue bornée
f
de S dans R,
On dit qu'une suite de variables aléatoires Xn à valeurs dans S
converge faiblement vers la variable aléatoire X si et seulement si
la suite (µn)n³ 0 des lois des v. a. Xn converge
faiblement vers la loi µ de X. La CNS de la définition se
traduit alors ainsi : pour toute fonction continue bornée f
de S dans R,
|
E |
[ |
f(Xn) |
] |
=E |
[ |
f(X) |
] |
. |
Il en découle immédiatement que
Propriété 1 [Corollaire fondamental]
Si Xn converge faiblement vers X, et si F est une fonction
continue de S dans T (deux espaces métriques), alors
F(Xn) converge faiblement vers F(X).
Proof.
Pour toute fonction f continue bornée de T dans R,
foF est continue bornée de S dans R, donc
|
E |
[ |
f |
( |
F(Xn) |
) |
] |
=E |
[ |
f |
( |
F(X) |
) |
] |
. |
Quelques exemples de fonctions continues sur S=C[ 0,1 ]
- Pour T=R ou Rd, et pour des nombres réels t, t1,
..., td fixés dans [ 0,1 ], les applications
f|®Ft(f)=f(t) et
f|®Ft®(f)=(f(t1),...,f(td)) sont
continues, donc Xn(t) X(t) et
| ( |
Xn(t1),...,Xn(td) |
) |
|
( |
X(t1),...,X(td) |
) |
. |
- f|®(maxf,minf,ò01f(t) dt) est
continue. Dans le cas du maximum, la convergence en loi de la hauteur
des arbres généraux apparaît alors comme une conséquence du théorème
clé, version Kaigh. Dans le même goût, la convergence en loi de la
largeur des arbres simples est une conséquence de la convergence du
profil, démontrée par Drmota et Gittenberger.
- f|®argmax f n'est pas continue
sur C[ 0,1 ], non plus que la suite des longueurs des intervalles
séparant les zéros de f (on parle de longueurs des
<< excursions >> de f).
En particulier, la convergence jointe de deux statistiques
intéressantes ne coûte pas plus cher que la convergence d'une seule.
Les derniers contre-exemples frustrants appellent un théorème relaxant
l'hypothèse de continuité sur F. Notons DF l'ensemble
des discontinuités de F.
Theorème 2 [Voir [2, Th. 5.1, p. 30]]
Si Xn X, et si P(XÎDF)=0, alors
F(Xn) converge faiblement vers F(X).
La démonstration utilise le théorème << porte-manteau >>, qu'on
verra un peu plus tard. Donnons deux exemples d'application :
- posons q(f)= sup { xÎ
[ 0,1 ] | f(x)=max[ 0,1 ]f }. Alors q
n'est pas continue sur C[ 0,1 ], Dq étant l'ensemble
des fonctions continues qui atteignent leur maximum en plus d'un
point. Il se trouve que le mouvement brownien standard B, avec
probabilité 1, atteint son maximum en un seul point de [ 0,1 ], donc
- posons Ta(f)=inf {x³ 0 | f(x)³ a },
l'infimum de l'ensemble vide étant par convention pris égal à
+¥ ; DTa est l'ensemble des fonctions f satisfaisant
f£ a sur un intervalle [ Ta(f),Ta(f)+h ],
h>0. Il se trouve qu'avec probabilité 1, Ta(B) est un point
d'accumulation de { t| Bt>a }, entrainant que
Les propriétés 3. et 4. du mouvement brownien sont des conséquences
plus ou moins directes de la propriété de Markov
forte4. De nombreux processus stochastiques
héritent5 des propriétés (1) et (2)
du mouvement brownien.
Les théorèmes de cette section permettent d'exploiter les résultats de
Donsker et al., mais réciproquement, joints avec des
considérations combinatoires, ils permettent de trouver ou de
retrouver les lois de fonctionelles intéressantes du mouvement
brownien et de ses avatars.
Exercices
- Posons Mn=max0£ k£ nSk. Montrer que pour k³ 0
P(Mn³ k)=P(Sn³ k+1)+P(Sn³ k).
Utiliser le Théorème central limite (version de Moivre6) pour en déduire que
| max { Bs|0£ s£ 1 } |
|
| B1|. |
P(Mn³ k et Sn³ l),
ce qui permet en prime d'obtenir la densité jointe de
(B1,max { Bs|0£ s£ 1 }).
- Notons q le lieu où le mouvement brownien atteint son
maximum. Montrer que q suit la loi de l'arcsinus, i. e.
pour 0£ a£ b£ 1,
| P |
( |
qÎ[ a,b ] |
) |
= |
ó
õ |
|
|
=
|
|
( |
arcsin(2b-1)-arcsin(2a-1) |
) |
. |
- Montrer que la valeur terminale du méandre brownien, m(1),
suit la loi de Rayleigh, à savoir, pour 0£ a£ b,
| P |
( |
m(1)Î[ a,b ] |
) |
= |
ó
õ |
|
xexp |
æ
ç
ç
è |
- |
|
ö
÷
÷
ø |
dx
= exp |
æ
ç
ç
è |
- |
|
ö
÷
÷
ø |
-exp |
æ
ç
ç
è |
- |
|
ö
÷
÷
ø |
. |
- Montrer que le lieu du maximum du pont brownien est uniformément
distribué sur [ 0,1 ]7. Y a-t-il une
démonstration combinatoire du fait que la valeur maximale du pont
brownien suit la loi de
Rayleigh8?
- Démontrer la formule (11.5) page 78 de [2].
En déduire la loi du maximum de l'excursion brownienne9.
4 Convergence faible : critères et autres caractérisations
Theorème 3 [Théorème << porte-manteau >>, voir [2, Th. 2.1,
p. 11]]
Xn converge faiblement vers X si et seulement si une des
conditions suivantes est remplie :
- limn E[f(Xn)]=E[f(X)] pour toute
fonction f continue bornée de S dans R ;
- limn E[f(Xn)]=E[f(X)] pour toute fonction
f bornée, uniformément continue, de S dans R ;
- limsupn P(XnÎ F)£ P(XÎ F) pour tout
fermé F de S ;
- liminfn P(XnÎ G)³ P(XÎ G) pour tout
ouvert G de S ;
- limn P(XnÎ A)= P(XÎ A) pour tout A de
S qui vérifie P(XÎ ¶ A)=0.
Ici encore on pourra se reporter à [2] pour les
développements. Une classe A de fonctions de S caractérise une
loi de probabilité si pour tout choix de deux variables X et Y à
valeurs dans S, on a
| " fÎA, E |
[ |
f(X) |
] |
=
E |
[ |
f(Y) |
] |
Þ X |
|
Y. |
Exemples
- Pour S= R, la fonction de répartition caractérise une loi de
probabilité, ce qui revient à dire que la classe A=
{1(-¥,x] | xÎ R}
est caractérisante.
- Pour S= Rd, la classe A= {Ft® | t®Î Rd}, où Ft® est défini
par
est caractérisante, t®|®E[eit®· X]
étant appelée fonction caractéristique de X.
- Pour S=C[ 0,1 ], C[ a,b ] ou C[ 0,+¥) la classe
A={ Ft® | d³ 1, t®ÎRd }, où
Ft® est défini par
| F |
|
(f)= |
( |
f(t1),...,f(td) |
) |
- La classe A des fonctions bornées et uniformément continues
de S dans R est caractérisante.
La convergence de E[F(Xn)] vers E[F(X)] pour
toutes les fonctions F d'une classe caractérisante A
suffit-elle à assurer la convergence faible de Xn vers X ? La
réponse est différente pour chacun des exemples ci-dessus : pour 2.
c'est oui, en vertu du Théorème de continuité de Paul
Lévy [2, Théorème 7.6, p. 46], et il s'agit d'une
CNS. Pour 1. c'est aussi oui, mais la condition est largement trop
restrictive : il s'agit d'une condition nécessaire seulement si la loi
limite est diffuse (i. e. P(X=a)=0 pour
tout a dans R), en vertu du 5. du Théorème
<< porte-manteau >>, puisque ¶(-¥,a ]={a} ! Enfin,
la réponse est non pour l'exemple 3., comme le montre l'exemple
suivant tiré de [2] : prenons X et Xn non
aléatoires à valeur dans C[ 0,1 ], Xº 0 et Xnº
fn, fn ayant le graphe ci-dessous :
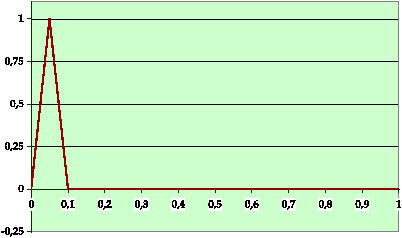
Figure 4:
fn est continue et affine par morceau,
avec ici pour
n=10,
(
f(0),
f(1/2
n),
f(1/
n),
f(1))=(0,1,0,0).
les distributions fini-dimensionelles de Xn
convergent bien faiblement vers les
probabilités concentrées sur 0Î Rd, i. e.
vers les distributions fini-dimensionelles de X, mais
F(Xn)=maxXnº 1 ne converge pas faiblement
vers F(X)=maxXº 0.
Il faut donc une condition supplémentaire à la
convergence des distributions fini-dimensionelles pour obtenir
la convergence faible des variables aléatoires à valeur dans
C[ 0,1 ] : c'est la condition de tension.
Definition 11
La suite de variables aléatoires Xn est tendue
(ou
équitendue
) si et seulement si pour tout e >0 il
existe un compact Ke de S tel que
" n, P(XnÏ Ke)
£e.
Le Théorème de Prohorov [2, Section 6] assure que la
tension est une CS (et une CNS si S=C[ 0,1 ]) pour la
relative compacité d'une suite de mesures de probabilité (ici
les lois des v. a. Xn). Il suit que cette suite de variables
(Xn)n³0 possède au moins une valeur d'adhérence pour la
convergence faible. On connait les distributions fini-dimensionelles
de cette valeur d'adhérence, ce sont les limites des distributions
fini-dimensionelles de Xn, donc ce sont les distributions
fini-dimensionelles de X, donc X est la seule valeur d'adhérence
de Xn, or une suite relativement compacte ayant une seule valeur
d'adhérence est convergente. Finalement :
Theorème 4
Si une suite de variables aléatoires Xn variables aléatoires à
valeurs dans C[ 0,1 ] est tendue, et si ses distributions
fini-dimensionelles convergent vers celles de X, alors Xn
converge faiblement vers X.
Le chapitre 2 de [2] donne une foule de critères de
tension dans C[ 0,1 ], basées sur la caractérisation
d'Arzelà--Ascoli des compacts de C[ 0,1 ]. Par exemple, les
démonstrations de Donsker, Iglehart et Kaigh sont basées sur de tels
critères, ainsi que la démonstration par Drmota et Gittenberger de la
convergence du profil des arbres simples. Il existe des traitements
plus modernes [10, 14, 15], mais
[2] est déjà très lisible et complet.
Il faut aussi parler du lien entre convergence presque sûre, en
probabilité, et dans Lp d'une part, convergence faible d'autre
part. Les premières citées exigent que les variables Xn et X, à
valeurs dans le même espace S à l'arrivée, soient aussi définie sur
le même triplet probabiliste (W, A, P) au
départ, alors que la convergence faible, étant en fait uniquement la
convergence de la mesure image par Xn vers la mesure image par X
des mesures de probabilité des espaces de départ, exige seulement que
Xn et X aient le même espace d'arrivée S. Notons
d(·,·) la distance sur S.
Definition 12
Une suite (Xn)n³ 0 converge :
-
presque sûrement vers X si et seulement si
| P |
æ
ç
ç
è |
ì
í
î |
wÎW |
|
|
d |
( |
Xn(w),X(w) |
) |
=0 |
ü
ý
þ |
ö
÷
÷
ø |
=1 ; |
- en probabilité vers X si et seulement si
| "e |
>0,
|
|
P |
( |
{ |
wÎW |
d |
( |
Xn(w),X(w) |
) |
³ e |
} |
) |
=0 ; |
- vers X dans Lp si et seulement si
Theorème 5
Les trois convergences ci-dessus entrainent la convergence faible.
Proof.
Seulement pour le 1., pour une fonction continue F,
F(Xn) converge presque sûrement vers F(X), et
si de plus F est bornée, le Théorème de convergence dominée
entraine bien que limn
E[F(Xn)]=E[F(X)]. Par
ailleurs, 3. entraine 2. en vertu de l'inégalité de Markov. Pour
montrer que 2. entraine la convergence faible, il faut utiliser la
caractérisation 2. du Théorème << porte-manteau >> et travailler à
peine un peu plus.
Finalement il y a une quasi-réciproque utile au théorème précédent,
c'est le
Theorème 6 [Théorème de représentation de Skorohod, voir
[18, II.86.1, p. 215]]
Si S est un espace de Lusin (en particulier pour S=C[ 0,1 ])
et si la suite de variables aléatoires (Xn)n³ 0, à valeurs
dans S, converge faiblement
vers X, alors il existe un
triplet probabiliste (W, A, P), et, définies sur ce
triplet, des copies (Xn^)n³ 0 et X^ de (Xn)n³
0 et de X, telles que (Xn^)n³ 0 converge
presque sûrement
vers X^.
Par << copie >>, on entend que Xn et Xn^, ou encore X et
X^, ont même loi. Par exemple, il n'est pas toujours naturel de
construire des arbres simples aléatoires, ou des graphes aléatoires,
de tailles différentes, sur le même espace de probabilité : il est
beaucoup plus fréquent de considérer, par exemple, l'ensemble Tn
des arbres étiquetés de taille n comme un espace de probabilité à
lui tout seul, muni de la probabilité uniforme. Plonger tous les
Tn dans un même triplet probabiliste évite pourtant parfois
certains calculs de lois fini-dimensionelles : ils sont remplacés par
des estimations plus faciles conduisant à une convergence presque
sûre10. Par ailleurs, le
Théorème de représentation de Skorohod est un outil très commode pour
les démonstrations de la Section 6.
5 Propriétés du mouvement brownien
Le but ici n'est certainement pas de donner de démonstration, mais, à
titre mnémotechnique, de montrer comment le mouvement brownien imite
les (ou hérite des) propriétés de la marche aléatoire simple
symétrique.
Accroissements indépendants et stationnaires
La marche aléatoire simple symétrique possède des accroissements
indépendants : sous µn, pour 1£ k1£ k2£...£ ki£
n,
(Y1+...+Yk1)^ (Yk1+1+...+Yk2)
^ ... ^ (Yki-1+1+...+Yki)
i. e.
Sk1^(Sk2-Sk1)^...^(Ski-Ski-1)
et stationnaires
| (Yk+1+...+Yk+l) |
|
(Y1+...+Yl) |
Le mouvement brownien aussi ! C'est-à-dire sous µ, pour 0£
t1£ t2£...£ ti£ 1,
Bt1^ (Bt2-Bt1)^ ... ^ (Bti -Bti-1)
et pour t³ 0, s³ 0,
Cela entraine la propriété de Markov faible.
Propriété 2 [Propriété de Markov faible]
Le nouveau processus W=(Ws)0£ s£ h, défini par
Ws=Bt+s-Bt
est indépendant de (Bs)0£ s£ t. De plus W a même loi que
(Bs)0£ s£ h.
La démonstration requiert
seulement de vérifier que pour chaque k, l, et pour
chaque suite de nombres réels
0<t1<t2<...<tk£ t et 0<s1<s2<...<sl£ h,
| (Bti)1£ i£ k^ (Wsi)1£ i£ l
et (Wsi)1£ i£ l |
|
(Bsi)1£ i£ l. |
(Bt1,Bt2-Bt1,...,Btk-Btk-1)^
(Ws1,Ws2-Ws1,...,Wsl-Wsl-1)
et de remarquer que
(Ws1,Ws2-Ws1,...,Wsl-Wsl-1)
=(Bt+s1-Bt,Bt+s2-Bt+s1,...,Bt+sl-Bt+sl-1).
Cette dernière égalité plus la stationnarité des accroissements
donne aussi l'égalité en loi.
Remarque
On a bien sûr t>0, h>0, et on doit pour
le moment imposer t+h£ 1, mais
cette dernière inégalité est en fait
superflue car il est naturel de définir le mouvement brownien
sur [ 0,+¥) (comme de définir la marche aléatoire simple symétrique
(Sk)k³ 0 pour chaque entier positif).
Une construction possible du mouvement brownien sur la
demi-droite des entiers positifs
Considérons par exemple une suite (B(n))n³ 0,
B(n)=(Bs(n))0£ s£ 1 de mouvements browniens
mutuellement indépendants11.
Définissons alors B=(Bt)t³ 0 comme un élément
aléatoire de C[ 0,+¥), tel que pour n£ s£ t£ n+1,
Bt-Bs=Bt(n)-Bs(n),
c'est à dire qu'on recolle les graphes (trajectoires) des B(n)
pour former le graphe de B. Il est alors facile de voir que B
hérite des B(n) l'indépendance des accroissements. Il en hérite
aussi la stationarité des accroissements, mais, pour le voir, il
faut parler un peu de la loi de ces accroissements.
Lois des accroissements du mouvement brownien
La formule de Stirling, fondamentale en combinatoire, est née des
travaux de de Moivre qui sont en quelque sorte un
premier pas vers le mouvement brownien12.
Posons
Sk+l-Sk=-l+2 Z.
Alors Z suit la loi binomiale (l,1/2), i. e. pour 0£ i£ l,
On sait, depuis que de Moivre
a démontré la formule de Stirling13, et l'approximation << gaussienne >> de la loi
binomiale14, que l'on peut écrire, pour
l=2ë sn/2û ~ ns,
|
P(Sk+l-Sk=2ë x(n)1/2 /2û)
=P |
æ
ç
ç
è |
|
Î |
é
ê
ê
ë |
|
|
,
|
|
ù
ú
ú
û |
ö
÷
÷
ø |
|
~ |
|
|
e-x2/2s
~ P |
æ
ç
ç
è |
N(s)1/2Î |
é
ê
ê
ë |
x- |
|
,x+ |
|
ù
ú
ú
û |
ö
÷
÷
ø |
,
|
| P |
( |
NÎ[ a,b ] |
) |
= |
ó
õ |
|
|
e-x2/2 dx. |
En d'autres termes, Sk+l-Sk/(n)1/2 a approximativement la même
loi que (s)1/2 N, à savoir, la loi normale (ou gaussienne)
centrée de variance s,
notée traditionellement N(0,s).
D'autre part, Sk+l-Sk/(n)1/2 est l'accroissement,
entre les points k/n
et, approximativement, k/n + s, de la fonction obtenue, à partir de
la marche aléatoire simple symétrique, par changement d'échelle brownien.
Par passage à la limite, on en déduit que
Propriété 3 [Accroissements gaussiens]
Indépendemment de t,
Notons
On peut voir ps(x,y) comme la densité de probabilité de x+(s)1/2 N, i. e., en vertu
de la propriété d'accroissements gaussiens indépendants, comme
la densité conditionelle de Bt+s, sachant que Bt=x.
On en déduit que
Propriété 4 [Distributions fini-dimensionelles du mouvement
brownien]
La densité de probabilité f de
(Bt1,Bt2,...,Btd) est donnée par la formule
f(x1,x2,...,xd)=pt1(0,x1) pt2-t1(x1,x2)
... ptd-td-1(xd-1,xd).
Une autre manière de caractériser les distributions
fini-dimensionelles du mouvement brownien est de remarquer que
(Bt1,Bt2,...,Btd) est un vecteur gaussien
centré, dont la loi est donc caractérisée par sa matrice de
covariance. On calcule facilement le terme général :
Cov(Bti,Btj)= min(ti,tj).
En effet, pour s£ t,
| Cov(Bs,Bt)=Cov(Bs,Bs)+Cov(Bs,Bt-Bs)
=Var(Bs)=Var |
( |
(s)1/2 N |
) |
=sVar(N)=s, |
Rappelons qu'une variable aléatoire X=(X1,X2,...,Xd)
à valeurs dans Rd
est un vecteur gaussien si et seulement si toutes les combinaisons linéaires
de ses composantes sont gaussiennes (ont même loi que m+s N,
pour un choix approprié de m et s), ou encore, si et seulement si X
est image par une transformation affine (disons, X=m®+AN®)
d'un vecteur N®=(N1,N2,...,Nk)
dont les composantes Ni sont i. i. d. et de loi N(0,1). Dans le cas
des distributions fini-dimensionelles du mouvement
brownien, on a m®=0, et
on peut exhiber A et N®, en posant
La loi d'un vecteur gaussien est caractérisée par l'espérance de
chacune de ses composantes et par sa matrice de covariance. Dans la
représentation affine ci-dessus, m® est le vecteur des
espérances des composantes, et la matrice de covariance est
G=tA A.
Definition 13
Un processus X dont les distributions fini-dimensionelles sont
gaussiennes est appelé processus gaussien. La loi du processus
est alors caractérisée par sa fonction moyenne
m(t)=E[Xt] et sa fonction covariance
G(s,t)=Cov(Xs,Xt).
Le mouvement brownien et, comme on le verra en Section 7, le pont
brownien, sont deux exemples de processus gaussiens centrés
(m(t)º 0). La fonction covariance du mouvement brownien est
G(s,t)=min(s,t).
Theorème 7 [Transformations des trajectoires du mouvement brownien]
Le mouvement brownien est préservé par les transformations suivantes :
-
Symétrie : W(1)=(-Bt)t³ 0 est un mouvement
brownien.
- Décalage : Pour t0³ 0,
W(2)=(Bt0+t-Bt0)t³0 est un mouvement brownien.
- Changement d'échelle : Pour c>0,
W(3)=(1/(c)1/2Bct)t³ 0 est un mouvement
brownien.
- Inversion du temps :
W(4)=(Wt(4))t³ 0 défini par
Wt(4)=tB1/t, pour t>0, et par W0(4)=0, est un
mouvement brownien.
Proof.
Chacun de ces processus est gaussien centré : il suffit de calculer sa
fonction covariance. Dans les quatre cas, on trouve
G(i)(s,t)=min(s,t). Reste un petit problème : la
continuité de W(4) en 0, qui n'est pas automatique. La loi forte
des grands nombres15 pour le mouvement brownien, stipule que
En conséquence
| P |
( |
{ |
wÎW | t®
Wt(4)(w) est continue en 0 |
} |
) |
=1. |
Temps d'atteinte
Le temps d'atteinte de la hauteur a>0, noté Ta,
est défini par
| Ta= |
ì
í
î |
| inf { t³0| Bt³ a } |
si l'ensemble n'est pas vide, |
| +¥ |
si l'ensemble est vide. |
|
|
Theorème 8
Ta a même loi que a2/N2, en particulier
P(Ta=+¥)=0.
Proof.
On a
|
P(Ta> t)=P |
( |
max { Bs|0£ s£ t }<a |
) |
=P |
æ
ç
ç
è |
max |
ì
í
î |
|
|
Bts | 0£ s£ 1 |
ü
ý
þ |
< |
|
ö
÷
÷
ø |
|
=P |
æ
ç
ç
è |
max |
{ |
Bs|0£ s£ 1 |
} |
< |
|
ö
÷
÷
ø |
=P |
æ
ç
ç
è |
| B1| < |
|
ö
÷
÷
ø |
=P |
æ
ç
ç
è |
|
>t |
ö
÷
÷
ø |
,
|
Definition 14
Une v. a. T à valeurs dans [ 0,+¥] est un temps
d'arrêt du mouvement brownien si et seulement si
{ w | T(w)£ t } est dans la tribu
engendrée par (Bs)0£ s£ t, en d'autre termes, si on peut
décider de la véracité de l'affirmation << T(w)£ t >> en
observant la trajectoire du mouvement brownien seulement jusqu'à
l'instant t (inclus).
En particulier, les temps d'atteinte Ta sont des temps d'arrêts.
Propriété 5 [Propriété de Markov forte,
cf. [12, Section 2.5]]
T étant un temps d'arrêt, le nouveau processus
WT=(WsT)0£ s, défini par
WsT=BT+s-BT
est indépendant de (Bs)0£ s£ T.
De plus WT a même loi que le mouvement brownien.
Quelques conséquences
-
Ta+b-Ta est le temps d'atteinte de b par le processus
WTa, il est donc indépendant de Ta et a la même loi que
Tb. En d'autres termes, le processus (Ta)a³ 0 est à
accroissements indépendants et stationnaires17.
- Presque sûrement, +¥ est un point d'accumulation
de l'ensemble des zéros du mouvement brownien : posons T le premier
zéro du mouvement brownien après l'instant 1 (i. e.
T=inf { t³ 1| Bt=0 }). La loi conditionelle de T
sachant que B1=a est la loi de Ta, donc T est presque sûrement
fini ; T est un temps d'arrêt donc WT est lui-même un mouvement
brownien et possède lui aussi un zéro après son instant 1 (donc B
possède un zéro après l'instant 2, etc.).
- De la même manière on voit que, presque sûrement,
+¥ est un point d'accumulation
de l'ensemble { t³ 0| Bt>0 }, ou de
l'ensemble { t³ 0| Bt<0 }. Ainsi, par inversion du temps,
0 est est un point d'accumulation
des ensembles { t> 0| Bt=0 }, { t>0| Bt>0 }
et { t>0| Bt<0 }.
- Ainsi Ta est est un point d'accumulation
des ensembles { t> Ta| Bt=a }, { t>Ta| Bt<a } et
{ t>Ta| Bt>a }. Cette toute dernière assertion implique la
relation (2).
Ce ne sont que quelques exemples d'application de
la propriété de Markov forte, mais en fait on l'applique
comme on respire, sans s'en rendre compte. On a
commencé à aborder la structure
de l'ensemble des zéros du mouvement brownien, alors mentionnons que
Theorème 9 [Structure de l'ensemble des zéros du mouvement
brownien]
Presque sûrement, l'ensemble des zéros du mouvement brownien est
fermé, non borné, sans point isolé, de mesure de Lebesgue nulle, et
possède 0 comme point
d'accumulation18.
Finalement, mentionnons
Quelques propriétés locales du mouvement brownien
Pour un chemin de Bernoulli f quelconque dans C[ 0,n ], on a
|
|
\vert |
f(k+1)-f(k) |
\vert |
2=b-a, |
|
|
|
f |
æ
ç
ç
è |
a+ |
|
ö
÷
÷
ø |
-
f |
æ
ç
ç
è |
a+ |
|
ö
÷
÷
ø |
|
2=b-a, |
| Vt(2)(P)= |
|
\vert |
Btk-
Btk-1 |
\vert |
2 |
Propriété 6 [Variation quadratique, cf. [12, Th. 1.5.8 et
Problème 2.5.5]]
En probabilité, Vt(2)(P) converge vers t quand ||
P|| tend vers 0, i. e.
pour chaque e ,h>0, on
peut trouver d>0 tel que || P||<d entraine
| P |
( |
\vert |
Vt(2)(P)-t |
\vert |
>e |
) |
<h. |
Ceci, avec le fait que presque sûrement sous µn une fonction
possède une dérivée dont la valeur absolue en tout point (sauf en
k/n) est (n)1/2, laisse à penser que le mouvement brownien a
peu de chances d'être dérivable en un point donné. En fait on a un
résultat beaucoup plus précis :
Theorème 10 [Paley, Wiener & Zygmund, 1933,
cf. [12, Th. 2.9.18]]
| P |
( |
{ |
wÎ W | la fonction
t® Bt(w) n'est dérivable nulle
part |
} |
) |
=1. |
Une autre propriété, que l'on peut aussi pressentir en générant des
chemins de Bernoulli aléatoires, illustre bien le comportement
erratique du mouvement brownien :
Theorème 11 [Dvoretzky, Erdös & Kakutani, 1961,
cf. [12, Th. 2.9.13]]
| P |
( |
{ |
wÎ W | la fonction
t® Bt(w) n'a aucun point de
croissance |
} |
) |
=1. |
Un point t est un point de croissance de f si on peut trouver
d>0 tel que pour tout yÎ[t-d,t] et tout
zÎ[t,t+d], f(y)£ f(t)£ f(z).
Cet aperçu des propriétés du mouvement brownien est à la fois très
incomplet et assez désordonné. Heureusement la littérature sur le
sujet est riche, et on pourra s'y reporter.
References
- [1]
-
Biane (Philippe), Pitman (Jim), and Yor (Marc). --
Probability laws related to the Jacobi theta and Riemann zeta
functions, and Brownian excursions. Bulletin of the American
Mathematical Society (New Series), vol. 38, n°4, 2001,
pp. 435--465.
- [2]
-
Billingsley (Patrick). --
Convergence of probability measures. --
John Wiley & Sons Inc., New York, 1968, xii+253p.
- [3]
-
Borodin (Andrei N.) and Salminen (Paavo). --
Handbook of Brownian motion---facts and formulae. --
Birkhäuser Verlag, Basel, 1996, xiv+462p.
- [4]
-
Chassaing (Philippe) and Marckert (Jean-François). --
Parking functions, empirical processes, and the width of rooted
labeled trees. Electronic Journal of Combinatorics, vol. 8, n°1,
2001, p. Research Paper 14. 19 pages.
- [5]
-
Csörgö (M.) and Révész (P.). --
Strong approximations in probability and statistics. --
Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York,
1981, 284p.
- [6]
-
Donsker (Monroe D.). --
An invariance principle for certain probability limit theorems. Memoirs of the American Mathematical Society, vol. 1951, n°6,
1951, p. 12.
- [7]
-
Erdös (P.) and Kac (M.). --
On certain limit theorems of the theory of probability. Bulletin
of the American Mathematical Society, vol. 52, 1946,
pp. 292--302.
- [8]
-
Flajolet (Philippe) and Odlyzko (Andrew). --
The average height of binary trees and other simple trees. Journal of Computer and System Sciences, vol. 25, n°2,
1982, pp. 171--213.
- [9]
-
Iglehart (Donald L.). --
Functional central limit theorems for random walks conditioned to
stay positive. Annals of Probability, vol. 2, 1974,
pp. 608--619.
- [10]
-
Jacod (Jean) and Shiryaev (Albert N.). --
Limit theorems for stochastic processes. --
Springer-Verlag, Berlin, 1987, xviii+601p.
- [11]
-
Kaigh (W. D.). --
An invariance principle for random walk conditioned by a late return
to zero. Annals of Probability, vol. 4, n°1, 1976,
pp. 115--121.
- [12]
-
Karatzas (Ioannis) and Shreve (Steven E.). --
Brownian motion and stochastic calculus. --
Springer-Verlag, New York, 1991, second edition,
xxiv+470p.
- [13]
-
Liggett (Thomas M.). --
An invariance principle for conditioned sums of independent random
variables. J. Math. Mech., vol. 18, 1968, pp. 559--570.
- [14]
-
Parthasarathy (K. R.). --
Probability measures on metric spaces. --
Academic Press Inc., New York, 1967, xi+276p.
- [15]
-
Pollard (David). --
Convergence of stochastic processes. --
Springer-Verlag, New York, 1984, xiv+215p.
- [16]
-
Rényi (A.) and Szekeres (G.). --
On the height of trees. Journal of the Australian Mathematical
Society, vol. 7, 1967, pp. 497--507.
- [17]
-
Revuz (Daniel) and Yor (Marc). --
Continuous martingales and Brownian motion. --
Springer-Verlag, Berlin, 1999, third edition,
xiv+602p.
- [18]
-
Rogers (L. C. G.) and Williams (David). --
Diffusions, Markov processes, and martingales. Vol. 1. --
John Wiley & Sons Ltd., Chichester, 1994, second
edition, xx+386p. Foundations.
- [19]
-
Spencer (Joel). --
Enumerating graphs and Brownian motion. Communications on Pure
and Applied Mathematics, vol. 50, n°3, 1997,
pp. 291--294.
- [20]
-
Yor (M.). --
Local times and excursions for brownian motion: a concise
introduction. --
Postgrado de Matemáticas, Facultad de Ciencias, Universidad Central
de Venezuala, Caracas, 1995, Lecciones en
Mathemáticas, vol. 1.
- *
- Notes de cours pour le cours donné pendant le groupe de
travail ALÉA'01 à Luminy (France).
- 1
- Pour un aperçu agréable du lien entre
mouvement brownien et fonctions spéciales, voir [1].
- 2
- cf. [5], lire l'introduction.
- 3
- Dans la suite, chaque fois que c'est nécessaire, pour
les chemins de Dyck p. e., on sous entendra que n est pair, et dans
ce cas on notera n=2n'.
- 4
- Pour (1), voir [12, preuve du Th. 2.9.12
p. 107]. Pour (2), voir la Section 5 de ce
mini-cours.
- 5
- en vertu du théorème de Cameron--Martin--Girsanov,
cf. [17, Ch. 8].
- 6
- Voir
Section 5.
- 7
- Utiliser le lemme cyclique attribué
parfois à Raney, parfois à Dvoretski ou à Motzkin.
- 8
- cf. [2, Section 11], mais on peut
sûrement trouver un raccourci (je n'ai pas eu le temps de m'en
assurer).
- 9
- C'est,
en particulier, la loi limite pour la hauteur ou la largeur des arbres
simples [8, 16].
- 10
- Voir par exemple [4].
- 11
- On peut par exemple définir une
telle suite comme un élément au hasard de C[ 0,1 ]N muni du
produit infini de mesures de Wiener µÄ N.
- 12
- un peu forcé,
le rapprochement, non ?
- 13
- dans Miscellanea
Analytica, 1730, voir http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/De_Moivre.html.
- 14
- dans Approximatio ad Summam Terminorum
Binomii a+b|n
in Seriem expansi, 1733.
- 15
- Pour une démonstration simple, voir
[12, Problème 9.3, p. 104 et Remarque 3.10, p. 15]. On peut
être plus précis sur le comportement du mouvement brownien en
+¥ : voir, [12, p. 112], la loi du logarithme itérée due à
Khintchine, 1933.
- 16
- Il se trouve que W(4) est indistinguable d'un
processus à valeurs dans C[ 0,1 ], voir
[12, Section 1.1].
- 17
- mais ses
trajectoires ne sont pas continues,
cf. [12, Section 6.2.A].
- 18
- cf. [12, Th. 2.9.6].
This document was translated from LATEX by
HEVEA.









