Classifying ECO-Systems and Random Walks

Cyril Banderier

Algorithms Project, INRIA Rocquencourt

Algorithms Seminar

September 27, 1999

[summary by Pierre Nicodème]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract
This talk presents a classification by rationality, algebraicity or transcendence of ECO-systems (Enumerating Combinatorial Objects) and of more general random walks. It is based on an article by Cyril Banderier, Mireille Bousquet-Mélou, Alain Denise, Philippe Flajolet, Danièle Gardy and Dominique Gouyou-Beauchamps [1].



1   Introduction

A generating tree is defined by a system (an axiom and a family of rewriting rules)
æ
è		 (s0), { (k)®(e1(k))(e2(k))...(ek(k)) }
 
k³0
ö
ø		 .     (1)
Here, the axiom (s0) specifies the degree of the root, while the productions ei(k) (with ei(k)>0) list the degrees of the k descendants of a node labelled k (note the constraint on the number of descendants of a node). Such a system constitutes an ECO-System.

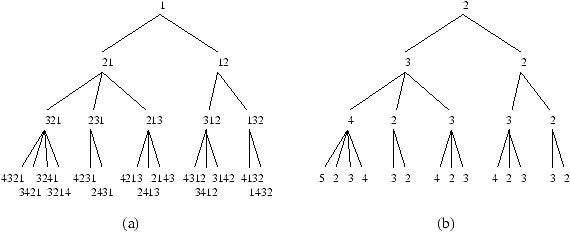
Example 1  123-avoiding permutations. Consider the set Sn(123) of permutations of length n that avoid the pattern 123: there exist no integers i<j<k such that s(i)<s(j)<s(k). For instance, s=4213 belongs to S4(123) but s=1324 does not, since s(1)<s(3)<s(4).

Observe that if tÎSn+1(123), then the permutation s obtained by erasing the entry n+1 from t belongs to Sn(123). Conversely, for every sÎSn(123), insert the value n+1 in each place where this is compatible with the avoiding rule; this gives an element of Sn+1(123). For example, the permutation s=213 gives 4213, 2413 and 2143, by insertion of 4 in first, second and third place respectively. The permutation 2134, resulting of the insertion of 4 in the last place, does not belong to S4(123). This process can be described by a tree whose nodes are the permutations avoiding 123: the root is 1, and the children of any node s are the permutations derived as above (see Figure 1(a)).

Let us now label the nodes by their number of children: we obtain the tree of Figure 1(b). It can be proved that the k children of any node labelled k are labelled respectively k+1,2,3,...,k. Thus the tree we have constructed is the generating tree obtained from the following system:
æ
è		 (2), { (k)®(2)(3)...(k-1)(k)(k+1) }
 
k³ 2
ö
ø		 .     (2)





Figure 1: The generating tree of 123-avoiding permutations: (a) nodes labelled by the permutations; (b) nodes labelled by the numbers of children.

Notations. We assume that all the values appearing in the generating tree are positive.

In the generating tree, let fn be the number of nodes at level n and sn the sum of the labels of these nodes. By convention, the root is at level 0, so that f0=1. In terms of walks, fn is the number of walks of length n. The generating function associated to the system is F(z) =ån³ 0 fn zn.

Note that sn=fn+1, and that the sequence (fn)n is nondecreasing.

Now let fn,k be the number of nodes at level n having label k (or the number of walks of length n ending at position k). The following generating functions will be of interest:
Fk(z) =
 
å
n³ 0
fn,k zn     and      F(z,u) =
 
å
n,k³ 0
fn,k zn uk.
We have F(z)=F(z,1)=åk³ 1Fk(z). Furthermore, the Fk's satisfy the relation
Fk(z) = [k=s0] + z
 
å
j³ 1
pj,k Fj(z),     (3)
where [k=s0] is 1 if k=s0 and 0 elsewhere and pj,k denotes the number |{ i£ j |  ei(j)=k }| of one-step transitions from j to k. This is equivalent to the recurrence fn+1,k=åj³ 1pj,k fn,j for the numbers fn,k (with f0,s0 = 1), that results from tracing all the paths that lead to k in n+1 steps.

We refer to [1] for random generation using counting and generating trees.

2   Rational Systems

ECO-systems satisfying strong regularity conditions lead to rational generating functions. This covers systems that have a finite number of allowed degrees, as well as systems where the sum of the labels at level k depends linearly on k.

Proposition 1   If finitely many labels appear in the tree, then F(z)=F(z,1) is rational.



Proof. Only a finite number of Fk's are nonzero; they are related by linear equations like Equation (3) above and therefore rational. F(z) is a finite sum of these, and is also rational.


Example 2   Fibonacci numbers are generated by the system ((1),{(k)®(k)k-1((kmod2)+1)}) that can also be written as ((1),{(1)®(2),(2)®(1)(2)}).

Proposition 2   Let s(k)=e1(k)+e2(k)+...+ek(k). If s is an affine function of k, say s(k)=a k+b, then the series F(z) is rational. More precisely:
F(z)=
1+(s0-a)z
1-a z-b z2
.

Proof. Let n³ 0 and let k1, k2,..., kfn denote the labels of the fn nodes at level n. Then
fn+2=sn+1
=(a k1+b)+(a k2+b) +...+(a k
 
fn
+b)
=a sn+b fn=a fn+1+b fn.
We know that f0=1 and f1=s0. The result follows.
Example 3   The system ((2),{(k)®(2)k-1(k+1)}) produces the Fibonacci numbers of even index.

Proposition 2 can be adapted to apply to systems that ``almost'' satisfy its criterion (see [1]).

3   Algebraic Systems

Systems where a finite modification of the set {1,...,k} is reachable from k lead to algebraic generating functions.

The possible moves from k are given by the rule:
(k)®{(0),...,(k-1)}\{(k-i)| iÎ B} È {{(k+j)| jÎ A}},     (4)
where AÌN and BÌN+ are a finite multiset (denoted {{...}}) and a finite set specifying respectively the allowed forward jumps (possibly coloured) and the forbidden backwards jumps.

Observe that these walk models are not necessarily ECO-systems, first because we allow labels to be zero---but a simple translation can take us back to a model with positive labels---, and second because we do not require (k) to have exactly k successors.

In this section fn,k is the number of walks of length n ending at point k and fn(u)=åk³ 0fn,kuk is the coefficient of zn in F(z,u).

We continue this section with the example A={4,15} and B={2}, axiom (0) and the corresponding family of rules
{ (k)®(0)(1)...(k-3)(k-1)(k+4)(k+15) } .
This corresponds in generating functions to substituting uk in
u0+...+uk-1-uk-2+uk+4+uk+15 =
1-uk
1-u
-uk-2+uk+4+uk+15
for k³ 2. This gives the recurrence fn+1(u)=fn(1)-fn(u)/1-u+(u4+u15-u-2)fn(u), and yields the functional equation
F(z,u)=1+z æ
ç
ç
è
F(z,1)-F(z,u)
1-u
+P(u)F(z,u)-{u<0}
 
å
n£ 0
zn L[fn](u) ö
÷
÷
ø		 .     (5)
Here P(u)=åaÎ Aua-åbÎ Bu-b and L[g](u)=g(1)-g(u)/1-u+P(u)g(u). Equation (5) may be rewritten as
F(z,u) æ
ç
ç
è		 1+
z
1-u
-zP(u) ö
÷
÷
ø		 =1+
z
1-u
F(z,1)-z
b-1
å
j=0
cj(u)uj F(z,0),
where the cj(u) are Laurent polynomials. The kernel K(z,u) of Equation (5) is the coefficient of F(z,u) in the left-hand side of this equation. F(z,u)K(z,u) is a linear combination of b+1 unknown functions. Solving K(z,u)=0 in u gives b+1 convergent branches ui(z) which, in turn, give the uj F(z,0) through a (b+1)×(b+1) linear system, and from there F(z,1), which is algebraic.
Proposition 3   The generating function F(z,1) counting the number of walks, starting from zero and irrespective of their endpoint is algebraic and F(z,1)=-1/zÕi=0b(1-ui), where b=max B and ui(z) are the finite solutions at z=0 of the equation K(z,u)=0.
Examples of algebraic systems are the Catalan numbers {(k)®(0)(1)...(k)(k+1)}, the Motzkin numbers {(k)®(0)...(k-1)(k+1)}, the Schröder numbers {(k)®(0)...(k-1)(k)(k+1)} or the m-ary trees ((m),{(k)®(m)...(k)(k+1)(k+2)...(k+m-1)}).

4   Transcendental Systems

4.1   Transcendence

If the coefficients of a series grow too fast, its radius of convergence is zero.
Proposition 4   Let b be a nonnegative integer. For k³1, let mk=|{ i| ei(k)³ k-b }|. Assume that:
  1. for all k, there exists a forward jump from k (i.e., ei(k)>k for some i),
  2. the sequence (mk)k is non-decreasing and tends to infinity.
Then the generating function of the system has radius of convergence 0.

Proof. See [1].
However, there are ECO-systems or walks that are transcendental with positive radius of convergence such as {(k)®(2)(4)...(2k)} or {(k)®(é k/2ù)k-1(k+1)}.

4.2   Holonomy

A subclass of transcendental functions is the class of holonomic functions. A series is said to be holonomic or D-finite if it satisfies a linear differential equation with polynomial coefficients in z. Equivalently, its coefficients fn satisfy a linear recurrence relation with polynomial coefficients in n. Given a sequence fn, the OGF (ordinary generating function) å fn zn is holonomic if and only if the EGF (exponential generating function) å fnzn/n! is holonomic.

The following table gives examples of holonomic and non-holonomic transcendental systems with references to the Encyclopedia of Integer Sequences (EIS) by Sloane and Plouffe [2, 3].

Axiom Rewriting rules Name EIS Id. Generating Function
  Holonomic OGF     EGF
(1) (k)® (k+1)k Permutations M1675 1/(1-z)
(2) (k)® (k)(k+1)k-1 Arrangements M1497 ez/(1-z)
(1) (k)® (k-1)k-1 (k+1) Involutions M1221 ez+z2/2
(2) (k)® (k+1)k-1 (k+2) Partial permutations M1795 ez/(1-z)/(1-z)
         
  Nonholonomic OGF     EGF
(1) (k)® (k)k-1 (k+1) Bell numbers M1484 eez-1
(2) (k)® (k-1)(k)k-2(k+1) Bessel numbers M1462 ---

References

[1]
Banderier (C.), Bousquet-Mélou (M.), Denise (A.), Flajolet (P.), Gardy (D.), and Gouyou-Beauchamps (D.). -- Generating functions for generating trees. Discrete Mathematics. -- 25 pages. To appear.

[2]
Encyclopedia of integer sequences. -- Available from http://www.research.att.com/~njas/sequences/.

[3]
Sloane (N. J. A.) and Plouffe (Simon). -- The encyclopedia of integer sequences. -- Academic Press Inc., San Diego, CA, 1995, xiv+587p.
This document was translated from LATEX by HEVEA.