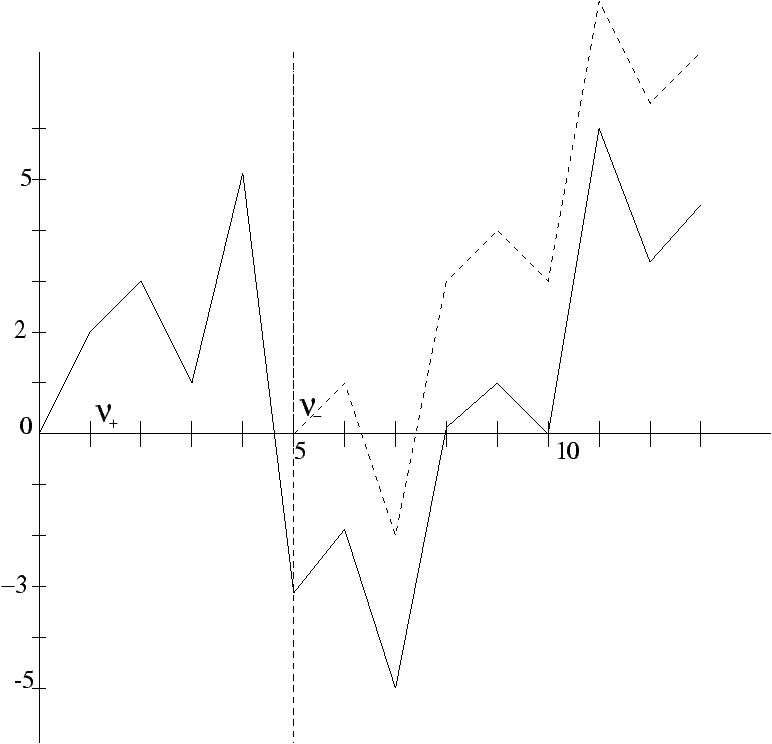Wiener-Hopf Factorization: Probabilistic Methods

Wiener-Hopf Factorization: Probabilistic Methods

Philippe Robert

Inria Rocquencourt

Algorithms Seminar

March 17, 1997

[summary by Jean-François Dantzer]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

1 Introduction

We consider a discrete random walk on Z, defined by

S₀=0 and

S_n=

i=1

X_i, n>0,

where (X_i)_{i³ 1} is an independent identically distributed (i.i.d.) sequence of random variables. We define two hitting times n₊ and n_-,

n₊=inf{k>0/S_k>0}, n_-=inf{k>0/S_k£ 0},

with the convention inf(Ø)=+¥.

Figure 1: Random walks (S_n)_{n³ 0} and (S_n+n_{_-})_{n³ 0} (in dotted line)

We also define M and L two variables indicating respectively the maximum of the random walk and the hit moments at which it is attained

sup

n³ 0

{S_n}, L=

inf

n³ 0

{S_n=M}.

This talk presents the classical probabilistic methods to derive the join distributions of (n₊,S_n_₊), (n_-,S_n_{_-}) and (M,L).

Applications of these results have been found in biology [3, 4] or in queueing theory [2]. For more details on this subject, see [1, 5].

2 Distribution of (n₊,S_n_₊) and (n_-,S_n_{_-})

The distributions of the pairs (n₊,S_n_₊) and (n_-,S_n_{_-}) will be expressed through their generating functions, i.e., E(uⁿ_⁺z^S_ⁿ_{_⁺}) and E(uⁿ_^-z^S_ⁿ_{_^-}).

We consider three variables

Y₊(u,z)

1-E(u

n₊

)

on {|u|<1,|z|£ 1},

Y_-(u,z)

1-E(u

n_-

)

on {|u|<1,|z|³ 1},

Y (u,z)

n³ 0

E(uⁿz

S_n

)

on {|u|<1,|z|= 1}.

The main result, the factorization of Wiener-Hopf described in the following proposition, gives an analytic characterization of Y₊ and Y_-.

Proposition 1

Y can be uniquely decomposed on {|z|=1} as:

Y (u,z)=Y₊ (u,z)Y_- (u,z),

where Y₊ and Y_- have the following properties:

Y₊ is analytic on {|z|<1};
Y₊ and 1/Y₊ are continuous and bounded on {|z|£ 1};
Y₊(u,0)=1;

and

Y_- is analytic on {|z|>1};
Y_- and 1/Y_- are continuous and bounded on {|z|³ 1}.

Proof. The proof is based on the following arguments:

The function Y can be expressed with the distribution of X₁, the sequence (X_i)_{n³ 1} is independent identically distributed, then E(Z^S_ⁿ)=E(Z^å_ⁱ⁼¹^ⁿ^X_ⁱ)=E(Z^X_¹)ⁿ, thus

Y (u,z)=

å

n³ 0
uⁿ E(z

X₁

)ⁿ=

1

1-uE(z

X₁

)

;
(S_n)_{n³ 0} and (S_n+n_{_-})_{n³ 0} have same distribution, (S_n+n_{_-})_{n³ 0} is the random walk beginning at the time n^-;
The independence between the pair (n_-,S_n_{_-}) and the sequence (S_n+n_{_-})_{n³ 0};
the same properties are also valid for (S_n+n_₊)_{n³ 0}.

3 Examples

The factorization is easy when Y has a finite number of poles and zeros. We consider two such examples.

3.1 Random walk ± 1

We suppose X_i=1 with probability p and X_i=-1 with probability (1-p). In that case,

Y(u,z)=

-upz²+z-u(1-p)

Y has only two poles

a₁(u)=

1-(1-4u²p(1-p))^1/2

2up

, a₂(u)=

1+(1-4u²p(1-p))^1/2

2up

with 0£a₁(u)£ 1£a₂(u).

The decomposition gives:

Y₊(u,z)=

a₂(u)

a₂(u)-z

and Y_-(u,z)=

a₂(u)up(z-a₁(u))

Here, we obtain the generating functions:

E(u

n₊

a₂(u)

, E(u

n_-

)=(1-a₂(u)up)+

u(1-p)

3.2 Random walk left bounded

We suppose Pr(X_i<-1)=0.

Y(u,z)=

1-uE(z^X)

z-uE(z^X+1)

In that case, the factorization is easy because by Rouché's theorem the function z|® z-uE(z^X+1) has one only root which belongs to {|z|<1}, which we denote by a (u). One proves that a (u)Î [0,1] and the decomposition of Y is the following:

Y₊(u,z)=

z-a (u)

z-uE(z^X+1)

uPr(X=-1)

a (u)

, Y_-(u,z)=

z-a (u)

a (u)

Pr(X=-1)

and the generating functions are:

E(u

n_-

)

=1-

uPr(X=-1)

a (u)

uPr(X=-1)

E(u

n₊

)

=1-

a (u)

uPr(X=-1)

z-uE(z^X+1)

z-a (u)

4 Distribution of the Maximum and its first Hitting time (M,L)

The distribution of the pair (M,L) is expressed through its generating function E(x^Lz^M).

Proposition 2

E(x^Lz^M)=

lim

u® 1

Y₊(ux,z)

Y₊(u,1)

Proof. We define the variables M_n and L_n, as

M_n=

max

0£ k£ n

S_k, L_n=inf{k/S_k=M_n},

and the function H on {|u|<1,|x|< 1, |z|< 1} as

H(u,x,z)=E(

n³ 0

uⁿx

L_n

M_n

Using the same arguments as in proposition 1, it can be proved that:

H(u,x,z)=

Y₊(ux,z)

Y₊(u,1)(1-u)

We conclude applying

lim

u® 1

(1-u)H(u,x,z)=

lim

u® 1

(1-u)E(

n³ 0

uⁿx

L_n

M_n

lim

n® +¥

E(x

L_n

M_n

)=E(x^Lz^M).

For the case of the random walk of subsection 3.1, it gives for p<1/2:

E(x^Lz^M)=

a₂(u)

a₂(u)-z

1-2p

1-p

then

Pr(L<+¥,M<+¥)=1,

and the distribution of M is geometric with parameter p/1-p, for p>1/2:

E(x^Lz^M)=0 and Pr(L=M=+¥)=1.

References

[1]: Feller (William). -- An introduction to probability theory and its applications. -- John Wiley & Sons, New York, 1971, 2nd edition, vol. II.
[2]: Iglehart (Donald L.). -- Extreme values in the GI/G/1 queue. Annals of Mathematical Statistics, vol. 43, n°2, 1972, pp. 627--635.
[3]: Karlin (Samuel) and Altschul (Stephen F.). -- Methods for assesing the statistical significance of molecular sequences features by using general scoring schemes. Proceedings of the National Academy of Sciences of the USA, vol. 87, 1990, pp. 2264--2268.
[4]: Karlin (Samuel) and Dembo (Amir). -- Strong limit theorems of empirical functionals for large exedances of partial sums of i.i.d. variables. Annals of Probability, vol. 19, n°4, 1991, pp. 1737--1755.
[5]: Spitzer (F.). -- Principles of Random Walk. -- Van Nostrand, 1964.

This document was translated from L^AT_EX by H^EV^EA.

1 Introduction

2 Distribution of (n+,Sn+) and (n-,Sn-)

3 Examples

3.1 Random walk ± 1

3.2 Random walk left bounded

4 Distribution of the Maximum and its first Hitting time (M,L)

References

2 Distribution of (n₊,S_n_₊) and (n_-,S_n_{_-})