Randomized Binary Search Trees

Conrado Martínez

Universitat Politecnica de Catalunya, Spain

Algorithms Seminar

December 9, 1996

[summary by Daničle Gardy]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract
Results on the performance of binary search trees are usually relative to the random permutation model. This talk presents a randomized version of the insertion and deletion operations on BST that ensures that, whatever the initial distribution of keys, results from the random permutation model apply.



1   Classical and randomized binary search trees

The usual model to analyze the performance of a binary search tree (BST) built on n keys assumes that all possible permutations are equally likely. This ensures that balanced trees have a ``large'' probability of appearing (a recent paper by Fill [2] gives a mathematical justification of this easy-to-understand fact), and that degenerate trees have a low probability; as a result it is well known that the search, insert or delete operations have expected time proportional to log n. But the assumption that the entries are inserted in random order does not always hold; moreover it is known that, under a specific sequence of insertions and deletions, the resulting tree is no longer random. Hence degeneracy of a BST is a real issue. Martínez and Roura propose here randomized versions of the insertion and deletion operations that ensure that, whatever the sequence of operations and the order of insertions and deletions of keys, the resulting binary search tree has the same probability as if it had been built on the random permutation model. As a consequence, the expected cost of operations on a randomized BST is guaranteed to be of order O(log n). Their work was first presented in [5]; a detailed version appears in [6].

1.1   Randomized insertion

The main idea is to use the split operation: This operation creates two BST's from a BST and a key, and can be used if one wishes to insert a key at the root of a BST. This algorithm is presented for example in [3, pp. 202--204]; it works by building two new BST's L and R from a key X and a given BST  A, which is destroyed by the operation: The first BST L contains the keys of A that are smaller than or equal to X, and the second BST R contains the keys of A that are larger than X. Then we insert X into a new node, whose left and right sons are L and R. An example is given in Figure 1.


Figure 1:

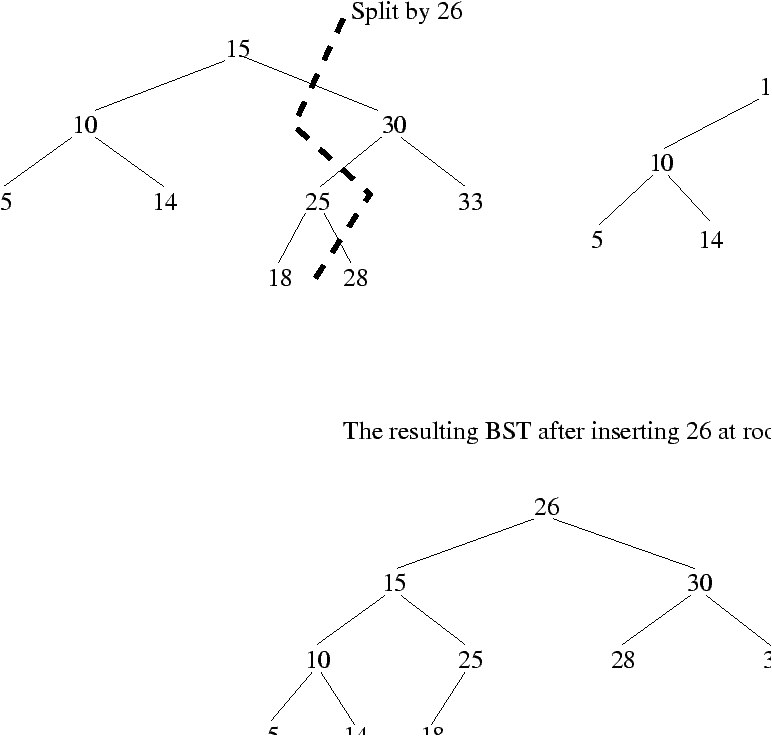
The randomized insertion works as follows
To insert a key X into a BST with n-1 keys, we use the insertion at root algorithm with probability 1/n, and with probability 1-1/n we insert the key recursively into the right or left subtree, according to the respective values of the key and the root.
The recursive insertion in a subtree is itself the randomized version; as a consequence, an insertion can happen at any place in the path from the root to the leaf where the key would be inserted if standard insertion were used.

1.2   Randomized deletion

As in the ``classical'' case without randomization, the deletion first searches for the key X to be deleted; the difference appears when deleting the key at the root of a tree. The deletion of the root is done here by the join algorithm of Martínez and Roura, which can be summarized as follows: An example is given in Figure 2.


Figure 2:

2   Performance analysis

For this analysis, we need to make precise the notion of random BST:
A BST on n keys is random if either it is empty (n=0), or the probability that a given key is at the root is 1/n, and the left and right subtrees are random.
This is exactly the BST built under the usual permutation model. The main point in the analysis of randomized BST is to show that insertions or deletions always yield a random BST if applied to a random BST, whatever the key to be inserted or deleted. Once this is done, results on random BST's apply: the average cost of an operation on a randomized BST is O(log n), for any sequence of operations on the tree.

3   Storage requirements

The randomized insertion and deletion both require storing in each node of the BST the size of the subtree rooted at this node, hence a memory requirement of order n. As a consequence of storing the number of nodes, randomized BST can also be used for ranking algorithms.

Each of the algorithms has an iterative version that uses only a constant number of auxiliary variables (no stack). The top-down implementation of the deletion algorithm requires that the size of each subtree be modified when the root is traversed; this can lead to problems if we try to delete a key that is not present in the tree. To avoid this, Martínez and Roura introduce an alternative scheme where each node stores the size of one of its subtrees (any of them) and an ``orientation'' bit that indicates the subtree whose size is kept; they also keep a single global variable with the total number of keys in the tree.

4   Conclusion

This elegant work solves the problem of degeneracy in BST, although the worst-case performance is still linear. Compared to balanced trees, algorithms for randomized BST are notably simpler; their performance can be compared with the behaviour of skip lists ([7], see also for example [1, 4] for the analysis of their performances).

The structure most closely related to randomized BST may well be the treap of Aragon and Seidel [8]: a BST is augmented with a priority for each key, in such a way that the tree is a search tree for keys, and a heap for priorities (a node has a larger priority than its sons). When priorities are chosen randomly, it is easy to see that an insertion, for example, can happen at any place on the path from the root to the leaf that would receive the new key in a BST with standard insertion at leaves. A main difference with the present work is that, while the randomness is related to the tree itself in the work of Martínez and Roura, in treaps it comes from the randomly chosen priority, which may appear less natural.

References

[1]
Devroye (L.). -- A limit theorem for random skip lists. Annals of Applied Probability, vol. 2, n°3, 1992, pp. 597--609.

[2]
Fill (James Allen). -- On the distribution of binary search trees under the random permutation model. Random Structures and Algorithms, vol. 8, n°1, 1996, pp. 1--25.

[3]
Froidevaux (Christine), Gaudel (Marie-Claude), and Soria (Michčle). -- Types de données et algorithmes. -- McGraw-Hill, Paris, 1990.

[4]
Kirschenhofer (P.) and Prodinger (H.). -- The path length of random skip lists. Acta Informatica, vol. 31, n°8, 1994, pp. 775--792.

[5]
Martínez (C.) and Roura (S.). -- Randomization of search trees by subtree size. In Díaz (J.) and Serna (M.) (editors), Proceedings of the 4th European Symposium on Algorithms (ESA). Lecture Notes in Computer Science, vol. 1136, pp. 91--106. -- Springer-Verlag, 1996.

[6]
Martínez (C.) and Roura (S.). -- Randomized binary search trees. -- Technical Report n°LSI-97-8, Departament de Llenguatges i Sistemes Informŕtics, Universitat Politecnica de Catalunya, Barcelona, 1997.

[7]
Pugh (William). -- Skip lists: a probabilistic alternative to balanced trees. In Dehne (F.), Sack (J.-R.), and Santoro (N.) (editors), Algorithms and data structures. Lecture Notes in Computer Science, vol. 382, pp. 437--449. -- Berlin, 1989. Proceedings of a Workshop held at Ottawa, 1989.

[8]
Seidel (R.) and Aragon (C. R.). -- Randomized search trees. Algorithmica, vol. 16, n°4-5, 1996, pp. 464--497.
This document was translated from LATEX by HEVEA.