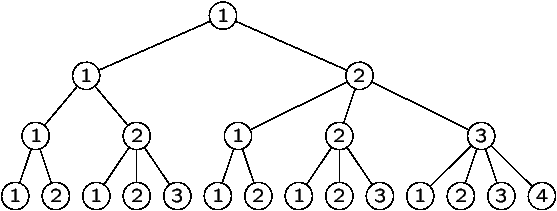The Tennis Ball Problem

Donatella Merlini

DSI, Università degli Studi di Firenze (Italy)

Algorithms Seminar

March 19, 2001

[summary by Cyril Banderier]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).
Abstract
Our object is to explore the ``s-tennis ball problem'' (at each round s balls are available and we play with one ball at a time). This is a natural generalization of the case s=2 considered by Mallows and Shapiro. We show how this generalization is connected with s-ary trees and employ the notion of generating trees to obtain a solution expressed in terms of generating functions. Then, we present a variation in which at each round we have 4 balls and play with 2 balls at a time. To solve this problem we use the concepts of Riordan arrays and stretched Riordan arrays, and a generalization of generating trees. This is a joint work by D. Merlini with D. G. Rogers, R. Sprugnoli and M. C. Verri.



1  Introduction

Let 1£ t<s be two integer numbers. A tennis player begins a match with 0 ball in the pocket. At each round, he is given s new balls, that he puts in the pocket, and throws away t balls, and so on until the nth round. The balls are labelled from 1 to sn and are served in increasing order. The tn balls thrown away form a sequence of tn labels. Two sequences which are equal once sorted are considered equivalent. The tennis ball problem consists in evaluating the following two quantities: the number fn of nonequivalent configurations after n rounds and the cumulative sum Sn (i.e., the sum---over all the possible configurations---of the labels of the tn balls that the player threw away).
Turns Balls received Balls in the pocket Balls thrown away
n=1 1 and 2 1 and 2 1
n=2 3 and 4 2, 3, and 4 3
n=3 5 and 6 2, 4, 5, and 6 2
n=4 7 and 8 4, 5, 6, 7, and 8 6
      sum = 1+3+2+6= 12
 
Turns Balls received Balls in the pocket Balls thrown away
n=1 1 and 2 1 and 2 2
n=2 3 and 4 1, 3, and 4 3
n=3 5 and 6 1, 4, 5, and 6 4
n=4 7 and 8 1, 5, 6, 7, and 8 1
      sum = 2+3+4+1= 10

Figure 1: Two scenarios for the (s=2,t=1)-tennis ball player.

The configuration after 4 rounds is (1, 2, 3, 6) for the first example and (1, 2, 3, 4) for the second example. In fact, for the (2,1)-case, one has f1=2, f2=5, f3=14, f4=... do you guess what? There is indeed 42 different configurations (after 4 rounds), and if one adds all the sums, one gets S1=1+2=3, S2=(1+2)+(1+3)+(1+4)+(2+3)+(2+4)=23, S3=131, S4=664, ...

In the next section, it is shown how the (s,1)-case can be solved in terms of s-ary trees (by symmetry, this also solves the (s,s-1)-case). Then, the last section is dedicated to the (4,2)-case, that the authors solved with Riordan arrays and a bilabelled generating tree technique.
Turns Balls received Balls in the pocket Balls thrown away
n=1 1, 2, 3, 4 1, 2, 3, 4 2, 3,
n=2 5, 6, 7, 8 1, 4, 5, 6, 7, 8 1, 7
n=3 9, 10, 11, 12 4, 5, 6, 8, 9, 10, 11, 12 10, 12
n=4 13, 14, 15, 16 4, 5, 6, 8, 9, 11, 13, 14, 15, 16 5, 16
      2+3+1+7+10+12+5+16= 56

Figure 2: A scenario for the (4,2)-tennis ball problem.

This is the only case solved with t¹ 1. The general (s,t)-tennis ball problem remains open.

2  The (s,1)-Tennis Ball Problem

Generating trees are a convenient way to reexpress the problem. Consider an infinite rooted tree T. The root (labelled 0 and corresponding to level 0) has t children (labelled 1,...,t). Each path in this tree corresponds to a scenario, thus each node at level n has a label which corresponds to the ball thrown away at round n. As we are counting the sorted configurations (that is, one does not care for the order of the balls thrown away), we can without loss of generality suppose that the labels increase with the depth.

Figure 3: The generating tree T for the (2,1)-case and an isomorphic tree T~.

More generally, the rewriting rule {
root: (1)
rule: (k) |® (1)...(k+s-2)...(k+s-1)
. describes the formation of a tree T~ which is isomorphic to the generating tree T of the (s,1)-case: a node with label b at level i in the generating tree T becomes a node with label si-b+1 in the tree T~.
Theorem 1   The number fn of configurations for the (s,1)-tennis ball problem is the number Tn+1 of s-ary trees with n+1 nodes. One has
Tn=
æ
è
sn
n
ö
ø
1+(s-1)n
  and   T(z)=1+zT(z)s .

Proof. The problem can be seen as the enumeration of walks on the integers (with an unbounded set of jumps described by the rewriting rule), for which the generating function can be made explicit [1]. Merlini et al. used Riordan array techniques [4].



Theorem 2   The cumulative sum (i.e., the sum over all the configurations of the labels of the thrown balls) is
Sn-1 =
sn2 +(s-1)n+1
2
æ
è
sn
n
ö
ø
(s-1)n+1
-
1
2
n
å
k=0
æ
è
sk
n
ö
ø
æ
è
s(n-k)
n-k
ö
ø
.

Proof. Consider An=åi=0n li,n, the sum of all the labels (with multiplicity) at level i in the tree T. The cumulative sum Sn satisfies
Sn=An-
(sn+2)(n+1)
2
Tn+1.
The generating function for the sequence An is:
A(z)=
s(s-1)zT'(z)2
2T(z)
+T'(z).
From these two equations, one gets the almost closed form of the theorem.

Note that the asymptotics of Sn can easily be deduced from the asymptotics of An.




These theorems are consistent with the fact that the (2,1)-case leads to Catalan numbers fn=(
2n
n
)/n+1 (proven in [2]) and to Sn=2n2+5n+4/n+2 (
2n+1
n
)-22n+1 (as it was found in [3] by hand manipulations of sums of binomial coefficients).

3  The (4,2)-Tennis Ball Problem

Here again, as one does not care for the order (of the balls thrown away), one can without loss of generality suppose that any configuration is represented by the smallest equivalent sequence with respect to lexicographical order. Thus the configuration (1,4),(5,8),(2,10) is considered to be the same as the configuration (1,2),(4,5),(8,10).

Let Mm[n] be the number of pairs at level n (in the bilabelled generating tree of the (4,2)-case) with larger element equal to m; one has the recurrence
Mm[n+1]=
m-2
å
r=2n
(m-r-1)Mr[n].

Defining fn,k=M4n+1-k[n] gives an infinite lower-triangular array:
n/k 1 2 3 4 5 6 7 8 9
0 1                
1 3 2 1            
2 22 16 10 4 1        
3 211 158 105 52 21 6 1    
4 2306 1752 1198 644 301 116 36 8 1




One has the relation fn+1,k+2=åj=0¥(j+1) fn,k+j. The sums fn=åk³ 1 fn,k give the sequence (1,6,53,554,...), the number of configurations for the (4,2)-tennis ball problem.

It is convenient to transform the above array into a proper Riordan array. A proper Riordan array is an infinite lower triangular array (Dn,k)n,kÎN which satisfies
dn+1,k+1=
¥
å
j=0
aj dn,k+j      for all n and k in N.
The generating function A(z)=åj aj zj allows to express dn,k by a Lagrangean-like formula
dn,k=[zn] g(z) ( zh(z) ) k where h(z)=A ( zh(z) ) .
The above array can be embedded in the array
n/k 0 1 2 3 4 5 6 7
0 1                
1 0 1              
2 1 1 1            
3 0 3 2 1          
4 6 6 6 3 1        
5 0 22 16 10 4 1      
6 53 53 53 31 15 5 1  

which satisfies A(z)=1/1-z, h(z)=C(z) (the generating function of Catalan numbers), and g(z)=2/2-zC(z)+zC(-z). In particular, the function g(z) generates the first column of this array and corresponds to the number of nonequivalent configurations one wants to enumerate: fn=gn=3(n+2)/(n+3)((2n+3)(
2n+4
n+2
)-4(n+1)/2/n+2(
n+3
(n+3)/2
) (for even n). The cumulative sum in the tree with root (0,0) and rewriting rule (k1,k2) |® (0,0)(0,1)...(k1+2,k1+2) is then given by
Sn=
n
å
h=0
 
å
r
µr[2n-2h] wr[2h]=
 
å
r
n
å
h=0
µr[2n-2h]wr[2h].
Here, µr[2n-2h] is the number of nodes at level n-h in the subtree starting with (r,*), and wr[2h] the total weight that the couples (r,*) have at level h. (Note that a label (k1,k2) at level n in the new tree corresponds to a label (4n-k2-1,4n-k1) in the generating tree of the (4,2)-case.) The Riordan array property yields µr(z) =g(z) C(z)r+2 and wr(z)=g(z)zr C(z)r+1 (zC(z)2+2r), thus
S(z)=
1
4
 
å
r
( µr(z)+µr(-z) ) ( wr(z)+wr(-z) ) =12z2 +284z4+5436z6+96768z8+O(z10).

The next nontrivial open cases are the (5,2)- and (5,3)-tennis ball problems. This is related to the enumeration of 2- and 3-dimensional constrained discrete random walks for which no closed form (or even recurrence) is known. Articles and slides related to this summary can be found at Donatella Merlini's web page http://www.dsi.unifi.it/~merlini/Publications.html.

References

[1]
Banderier (C.), Bousquet-Mélou (M.), Denise (A.), Flajolet (P.), Gardy (D.), and Gouyou-Beauchamps (D.). -- Generating functions for generating trees. Discrete Mathematics. -- 25 pages. To appear.

[2]
Grimaldi (Ralph P.) and Moser (Joseph G.). -- The Catalan numbers and a tennis ball problem. In Proceedings of the Twenty-eighth Southeastern International Conference on Combinatorics, Graph Theory and Computing (Boca Raton, FL, 1997), vol. 125, pp. 65--71. -- 1997.

[3]
Mallows (Colin L.) and Shapiro (Lou). -- Balls on the lawn. Journal of Integer Sequences, vol. 2, 1999. -- Article 99.1.5.

[4]
Merlini (D.), Rogers (D. G.), Sprugnoli (R.), and Verri (M. C.). -- The tennis ball. -- 2001. Submitted.
This document was translated from LATEX by HEVEA.