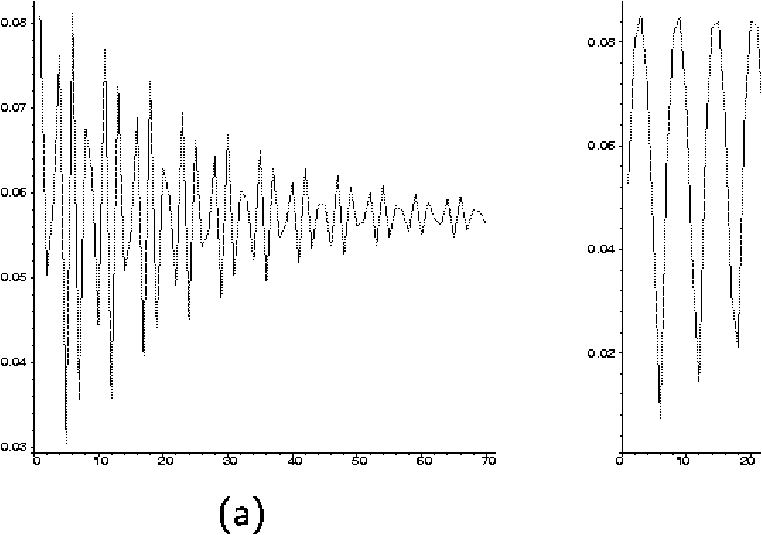
Figure 1: Huffman code redundancy for a memoryless source with control
parameter a=lg(1/p-1): (a) irrational case (p=1/p);
(b) rational case (p=1/9).
| H(P):=- |
|
ps lg ps, |
| h= |
|
- |
|
|
P(x1n)lg P(x1n). |
| h= |
|
pi |
|
pi,jlg pi,j, |
| Rn(C,P;x1n):=L | ( | C(x1n) | ) | +lg P(x1n), |
Louchard and Szpankowski (1997), Savari (1997), Wyner (1998), and Jacquet--Szpankowski (1995) proved that the Lempel--Ziv algorithms under either a memoryless or a Markov model have rates that are Q(n/log n) for LZ'783 and Q(nloglog n/log n) for LZ'77. The proofs provide detailed asymptotic information on the redundancy. The results again involve subtle fluctuations. The analysis is close to that of digital tries, with Mellin transforms playing a prominent rôle.
Figure 1: Huffman code redundancy for a memoryless source with control parameter a=lg(1/p-1): (a) irrational case (p=1/p); (b) rational case (p=1/9).
| An := |
|
|
P(x1n) = |
|
|
æ ç ç è |
|
ö ÷ ÷ ø |
|
æ ç ç è |
|
ö ÷ ÷ ø |
|
. |
| An= |
|
[zn] |
|
where T(z)=zeT(z) |
| An~ |
|
|
~( |
|
)1/2 and lg An= |
|
lg n+lg( |
|
)1/2+o(1). |
| rn= |
|
|
|
æ ç ç è |
|
ö ÷ ÷ ø |
|
æ ç ç è |
|
ö ÷ ÷ ø |
|
... |
æ ç ç è |
|
ö ÷ ÷ ø |
|
. |
| S(z,u):= |
|
b(ziu) where b(z)= |
|
. |
| lg rn = |
|
( |
æ ç ç è |
|
-1 |
ö ÷ ÷ ø |
n)1/2 - |
|
lg n + |
|
lg log n +O(1), |
http://www.cs.purdue.edu/people/spa.This document was translated from LATEX by HEVEA.