Queues, Stacks, and Transcendentality at the Transition to Chaos

Cristopher Moore

Computer Science Department, University of New Mexico

Algorithms Seminar

September 20, 1999

[summary by Bruno Salvy]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Iteration of the logistic map
F
 
µ
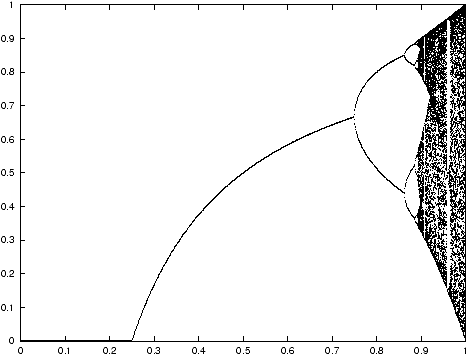
(x)=4µ x(1-x),    µÎ[ 0,1)
is a classical example of a discrete dynamical system exhibiting chaos. Depending on the value of µ, the iterates of an arbitrary xÎ I=[ 0,1 ] are attracted to a limit cycle of size a power of 2 (see [3]). Figure 1 displays the values of Fµ50(1/2),...,Fµ100(1/2) as µ increases from 0 to 1, where Fk denotes the kth iterate of F. Figure 2 shows an example of a trajectory with an attracting 4-cycle.



Figure 1: The period-doubling phenomenon.



Figure 2: 100 iterates for µ=0.884.

To each xÎ I is associated the infinite word a(x)Î{0,1}* whose kth letter is 0 if Fµk(x)£1/2 and 1 otherwise. The aim of Cristopher Moore and Porus Lakdawala [6] is to study the language L formed by the set of prefixes of all a(x) for xÎ I (the symbolic dynamics of Fµ) and its evolution as µ increases from 0 to 1. For instance, the language corresponding to µ in Figure 2 is
L=0
*
 
1
*
 
(10)
*
 
(1011)
*
 
.
This can be interpreted as follows: the first iterates can be smaller than 1/2, but apart from the fixed point at 0 (where a(0)=0*) they eventually get larger. Then, apart from the second fixed point of Fµ (where a is 1*) the iterates are attracted by the 4-cycle, but they may first have a few iterates on the other side of 1/2, hence the (10)*. One should also account for those prefixes which do not end exactly at the end of a period; this is obtained by concatenating (e|1|10|101) at the end of L and removing (1|10) which otherwise would be counted twice. However, these modifications introduce unnecessary technicalities and will be ignored in what follows. When µ increases further, the 4-cycle becomes repelling and gives rise to an attracting 8-cycle. This does not change L until the third element of the cycle becomes smaller than 1/2, and then
L=0
*
 
1
*
 
(10)
*
 
(1011)
*
 
(10111010)
*
 
.
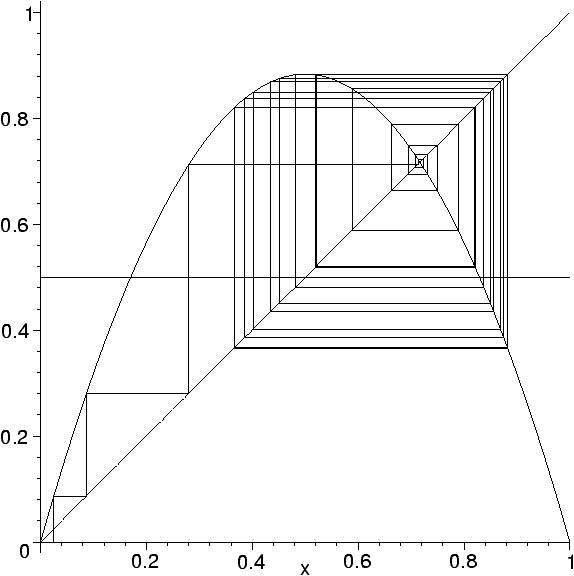
Examples of corresponding 8-cycles are given in Figure 3 and 4.


Figure 3: Limit cycle for µ=0.887.



Figure 4: Limit cycle for µ=0.89.

1   Transcendentality at the Transition to Chaos

This process leads to a sequence of languages
L0=0
*
 
,   L1=L0w
*
 
0
,   L2=L1w
*
 
1
,...,     (1)
with w0=1 and wn+1=R(wn) where R is the substitution
R:0|®11,1|®10.     (2)
Each of these languages is regular. Their generating functions are obtained by translation from (1):
L0(z)=
1
1-z
,     Ln(z)=Ln-1(z)
1
1-z
2n
 
.

The transition to chaos corresponds to letting µ approach 1. The limiting value of wn is the fixed point of R, the Morse sequence. The limiting value of L has a generating function defined by
L
 
¥
(0)=1,     L
 
¥
(z)=
L
 
¥
(z2)
1-z
.     (3)
From this it follows that L¥(z) has an infinite number of singularities on the unit circle, thus L¥(z) is not algebraic and the corresponding language is not context-free. This generating function is classical: it is the generating function of binary partitions studied by Mahler [5] and de Bruijn [2] who showed that the logarithm of the nth Taylor coefficient of L¥ behaves asymptotically like
1
2log2
æ
ç
ç
è		 log
n
log n
ö
÷
÷
ø
2



 
+ æ
ç
ç
è
1
2
+
1
log 2
+
loglog2
log2
ö
÷
÷
ø		 log n
- æ
ç
ç
è		 1+
loglog2
log2
ö
÷
÷
ø		 loglog n+F æ
ç
ç
è
log n-loglog n
log 2
ö
÷
÷
ø		 +o(1),
where F is a periodic function with period 1 for which a full Fourier expansion is known.

2   Stacks of Stacks

Since the language L¥ is not context-free, it cannot be recognized with a finite amount of memory. The question addressed by Moore and Lakdawala is to determine how simple a long-term memory mechanism recognizing L¥ can be. This in turn is expected to give more precise information on the nature of the transition to chaos. Two natural candidates for the mechanism are the queue (first in--first out) and the stack (last in--first out).

Since context-free languages are those recognized by automata with a stack (pushed-down automata) [4], a stack is not sufficient to recognize L¥. A more general class of languages is provided by indexed languages [4, p. 389], whose grammars look like context-free grammars except for string indices, which can be appended to non-terminals. Production rule involving an indexed non-terminal copies this index to all non-terminals it produces. For instance, { anbncn| n³0 } is not context-free but it is indexed, the grammar being



From the start state, the first rule introduces a final g, the second one stacks any number of f's to produce Tfng. The third rule then produces AfngBfngCfng, the rules on the second line pop these indices and the final g is popped by the rules on the third one. More generally, these languages are recognized by nested stack automata which resemble stacks of stacks.

It turns out that L¥ can be recognized by such a grammar:



The first rule takes care of the initial 0*, the second one first stacks a number k of f's at the end and then either produces an Afkg or an AfkgTfk. To this final Tfk, more f's can then be stacked by that same rule. To see that L¥ is the end result, it is then sufficient to show why Afkg actually produces the word wk from (1). This follows from productions in the second line performing the substitution R from (2).

3   Queues

Automata with k queues can simulate the k tapes of a multi-tape Turing machine. However, restricting the way the queues are accessed by imposing a bound on the number of transitions performed for each symbol of the input string leads to the class of quasi-real-time queue automata [1]. The corresponding grammars are breadth-first grammars. In these grammars, a production of the form A® sB where s is a string of terminals and B a string of non-terminals rewrites a string xAy into xsyB and the rule has to be applied to the leftmost non-terminals first. Thus the string of non-terminals represents the queue and the string of terminals represents the part of the input that has been read so far.

By storing the current wn on the queue and applying R when necessary to expand it, Moore and Lakdawala show that L¥ is recognizable by a real-time deterministic queue automaton with one queue.

4   Stacks

Again, with no time restriction, two stacks are sufficient to simulate a universal Turing machine. Exploiting the fact that wn is a palindrome except for its last symbol, it can be shown [6] that L¥ can be recognized by a real time automaton with two stacks.

The conclusion [6] is therefore that since one queue is sufficient while two stacks are necessary, the long-term memory of the system has more of a FIFO character. It is unclear however how much of this work can be generalized to other dynamical phase transitions.

References

[1]
Cherubini (Alessandra), Citrini (Claudio), Crespi-Reghizzi (Stefano), and Mandrioli (Dino). -- QRT FIFO automata, breadth-first grammars and their relations. Theoretical Computer Science, vol. 85, n°1, Algorithms Automat. Complexity Games, 1991, pp. 171--203.

[2]
De Bruijn (N. G.). -- On Mahler's partition problem. Indagationes Mathematicae, vol. 10, 1948, pp. 210--220. -- Reprinted from Koninkl. Nederl. Akademie Wetenschappen, Ser. A, vol. 51, 1948.

[3]
Devaney (Robert L.). -- An introduction to chaotic dynamical systems. -- Addison-Wesley Publishing Company Advanced Book Program, Redwood City, CA, 1989, second edition, xviii+336p.

[4]
Hopcroft (John E.) and Ullman (Jeffrey D.). -- Introduction to automata theory, languages, and computation. -- Addison-Wesley Publishing Co., Reading, Mass., 1979, x+418p. Addison-Wesley Series in Computer Science.

[5]
Mahler (Kurt). -- On a special functional equation. Journal of the London Mathematical Society, vol. 15, 1940, pp. 115--123.

[6]
Moore (Cristopher) and Lakdawala (Porus). -- Queues, stacks, and transcendentality at the transition to chaos. Physica D, vol. 135, n°1-2, 2000, pp. 24--40.
This document was translated from LATEX by HEVEA.