What is the Complexity of a Random Map?

What is the Complexity of a Random Map?

Kevin Compton

University of Michigan

Algorithms Seminar

March 29, 1999

[summary by Gilles Schaeffer¹]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

This talk presents a joint work with Ed Bender and Bruce Richmond [2].

1 Introduction

A class of structures obeys a 0--1 law if every first-order sentence has an asymptotic probability of 0 or 1 within the class. Techniques used to prove 0--1 laws are closely related to average-case analyses of algorithms. For example, Abiteboul, Compton and Vianu [1] showed that the 0--1 law for random relational structures (which includes random graphs with constant edge probabilities) can be used to give an average-case analysis of certain database query optimizations. However, the random graph model is not a very realistic model for databases, so it is useful to examine other structures. A map, or embedding of a graph into a surface of fixed genus, may be a better model of certain kinds of geometric databases. Here we show that the class of random maps in surface of fixed genus obeys a 0--1 law. The proof is based on game strategies and keeping track of anchors.

2 First Order Logic on Maps

A map is an embedding of a connected graph G in a surface S such that all components of S\ G are simply connected regions called faces. Maps are considered up to homeomorphisms of the surface taking vertices to vertices, edges to edges and faces to faces.

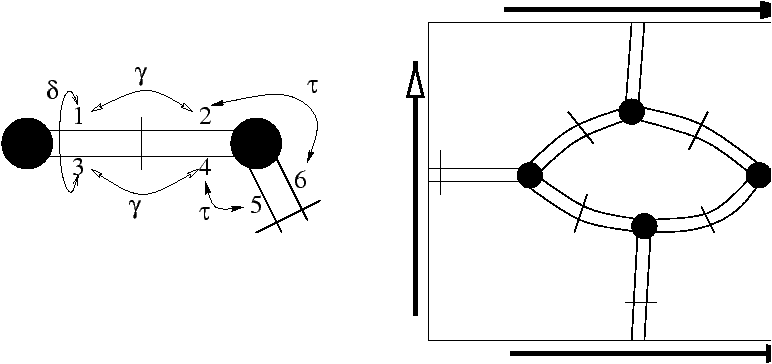
Like graphs, maps with a finite number of edges can be given various combinatorial representations. We shall use the cross representation, introduced by Tutte [9]: each edge is viewed as a fat ribbon with four corners or crosses (see Figure 1), and three fix-point free involutions are defined on the set A_c of crosses. The first two, g and d, relate two by two the four adjacent crosses of each edge, g along faces and d along vertices. The last one, t, relates pairs of crosses sharing an incidence between a face and a vertex. The structure á A_c,g,d,tñ completely defines the map: for instance, vertices, faces and edges are respectively described by the orbits of the subgroups ág,tñ, ád,tñ and á g,dñ.

Figure 1: Illustration of the action of the three involutions on the four corners or crosses of edges, and two different drawings of the same map on the torus.

Now let us consider the vocabulary S₁ consisting of a set of constants and the binary relations G, D and T. A map á A_c,g,d,tñ can then be seen as a structure over S₁, where the constants are taken in A_c and the binary relations are interpreted as the respective graphs of the three involutions. Our interest is in properties expressible by first order formulas on these structures. In order to allow quantification on vertices and faces, and not only on crosses, we enrich the vocabulary with two other sets of constants (for vertices and faces) and two other binary relations I and J, respectively interpreted as the incidence relations between vertices and crosses and between crosses and faces. For convenience the binary relation E is also added to describe crosses that belong to the same edge (although E could be expressed in terms of G, D and T). Let S be this extended vocabulary.

For instance, the following sentence (i.e., formula without free variable) is satisfied by maps containing a cycle of length three:

$ v₁,v₂,v₃ $ c₁₂,c₂₁ c₁₂¹ c₂₁Ù E(c₁₂,c₂₁)Ù I(v₁,c₁₂) Ù I(v₂,c₂₁)

Ù $ c₁₃,c₃₁ c₁₃¹ c₃₁Ù E(c₁₃,c₃₁)Ù I(v₁,c₁₃) Ù I(v₃,c₃₁)

Ù $ c₂₃,c₃₂ c₂₃¹ c₃₂Ù E(c₂₃,c₃₂)Ù I(v₂,c₂₃) Ù I(v₃,c₃₂).

In the study of asymptotic 0--1 laws for random structures (here maps), we consider a class of structures C on S, with the uniform measure µ_n on the set C_n of structures of size n (here maps with n edges). Our interest is in the limit when n goes to infinity of

µ_n(f)=µ_n({ AÎ C_n | A|=f}).

If this limit exists, it is called the asymptotic probability of f and denoted µ(f).

A class of structures has an asymptotic first order 0--1 law if all first-order sentences have an asymptotic probability of either 0 or 1.

3 0--1 Laws and the Ehrenfeucht-Fraïssé Game

A classical logical tool to prove 0--1 laws is the Ehrenfeucht-Fraïssé game: essentially this game is used to show that if two structures have the same kinds of local substructures then they satisfy the same first-order sentences of given quantifier rank.

The quantifier rank of a formula is the maximal number of stacked quantifiers in the formula (e.g. the previous example has rank 5). Given two maps A and B, we write Aº_m B if they satisfy the same formulas of rank at most m. Remark that the number of inequivalent formulas of given rank over S is finite, so that the number of equivalence classes for º_m is finite, a fact that we shall use in Section 4. The following proposition is only a matter of rephrasing:

Proposition 1 A class of structure C has an asymptotic first order 0--1 law if and only if for all m there exists an equivalence class E_m of º_m, such that

lim

n®¥

µ_n ({ AÎ C_n| AÎ E_m})=1.

Therefore, in order to prove a 0--1 law, one should define, for all m, a large enough class E'_m in which maps cannot be distinguished by rank m formulas. Here come the Ehrenfeucht-Fraïssé game in play: There are two players, Spoiler and Duplicator, playing m rounds on two structures (here maps) A and B. Spoiler starts each round by picking an element (a cross, a vertex or a face) in one of the maps and Duplicator responds by picking an element of the same kind in the other map. These 2m elements are viewed as interpretations d₁^A,...,d_m^A and d₁^B,...,d_m^B of some fresh constants d₁,...,d_m. After m rounds, Duplicator wins if the two extended structures over SÈ{d₁,...,d_m} cannot be distinguished by atomic formulas (i.e., without quantifier).

Theorem 1 [Fraïssé, Ehrenfeucht] Let A and B be two structures over S. Duplicator has a winning strategy in the m-round game if and only if Aº_m B.

Hence we look for a large enough class E'_m on which we can describe a winning strategy for Duplicator. As suggested by the classical approach, we want to consider the class of structures that contain many copies of all possible kinds of local substructures. In such a structure Duplicator will always be able to find a local substructure on which to imitate Spoiler.

4 Distance and Richness in Maps

In order to formalize the idea of local substructures for maps we are led by existing results on random maps to consider:

Distances in the derived map: a proper notion of distance can be defined (which is somewhat more complicated than distance on graphs) so that all relations of S are local (i.e., they are false as long as elements are at a distance greater than, say, two).
Planar balls: the substructures we consider are the finite radius balls (in the sense of the previous distance) which are planar.

While it is natural to define a distance and consider finite radius balls, the planarity assumption may be surprising. It comes from the theory of random maps: many families of maps (on surfaces of given genus) have the large representativity property, asserting that for a given d, in almost all maps, the balls of diameter d are planar submaps. All the families C of maps we will consider then have the following richness property:

Property 1 [Richness] Let P be a fixed planar map occurring as a submap of some map in our family C, and k be a non-negative integer. Then

µ(" a₁,...,a_k $ a submap isomorphic to P not containing a₁,...,a_k)=1

where a₁,...,a_k range over all vertices, faces and crosses.

At each round of the game, our Duplicator will need to use richness to choose an element with a neighborhood isomorphic to the neighborhood of the element chosen by Spoiler. Unfortunately, given a diameter d, there are infinitely many possible planar balls with this diameter, so that the richness property is not sufficient. Instead of requiring Duplicator to choose an isomorphic neighborhood, we will content with a neighborhood that is indistinguishable by rank-m-sentences. As there are only a finite number of º_m-equivalence classes of planar balls with given diameter d, Duplicator will only have to make his choice in a finite set of representative B₁,..., B_k.

We are now in a position to define the class of maps E'_m on which Duplicator has a winning strategy: let m be fixed, and consider the set of maps such that, for each B_i and a₁,...,a_k as above, there exists a submap isomorphic to B_i avoiding a₁,...,a_k. As there are finitely many B_i, Property 1 implies that this set E'_m is large enough, i.e., satisfies

lim

n®¥

µ_n({ AÎ C_n| AÎ E'_m})=1.

Therefore we need to prove that Duplicator has a winning strategy for all couples of maps in E'_m.

5 Winning Strategy and the Good Use of Anchors

The strategy for Duplicator associates a security zone to each chosen element with the following requirements:

The security zone of an element e chosen at round i contains all elements at distance at most 2^m-i+1 of e.
The security zones of the two elements chosen at each round are indistinguishable (i.e., belong to the same º_m-equivalence class).

Suppose now Spoiler chooses element e at round i; there are two cases:

if no previously chosen element is in the security zone Z of e, then Duplicator chooses any element e' in the other map with a security zone Z' indistinguishable from Z, and disjoint from previously chosen zones. In this case, e and e' are their own anchor. The assumption on E' assures that this is always possible.
if a previously chosen element f is in the security zone of e, then there is a chance that they interact. In this case, let g be the anchor of f. It is easy to see that e belongs to the security zone of g, because the sizes of the zones are exponentially distributed. Therefore Duplicator can choose the image e' of e in the zone Z' associated to the security zone Z of g. The anchors of e and e' are respectively set to be g and g'.

At the end of the game, elements in A are either too far away to interact or share the same anchor. In both cases the corresponding elements in B will satisfy the same atomic formulas.

6 Conclusion

Richness properties have been proved for many families of rooted maps by Bender et al. [4, 3, 5, 6, 7]. Thanks to the work of Richmond and Wormald [8] these results hold as well for unrooted maps. Using the previously described machinery it implies 0--1 laws for the following families of maps on a surface of given genus: all maps, smooth maps, 2-connected maps, 3-connected maps, triangular maps, 2-connected triangular maps and 3-connected triangular maps.

References

[1]: Abiteboul (S.), Compton (K. J.), and Vianu (V.). -- Queries are easier than you though (probably). In Proceedings of the ACM Symposium on Principle of Database Systems. pp. 32--42. -- Association for Computing Machinery, 1992.
[2]: Bender (E. A.), Compton (K. J.), and Richmond (L. B.). -- 0-1 laws for maps. Random Structures & Algorithms, vol. 14, n°3, 1999, pp. 215--237.
[3]: Bender (E. A.), Gao (Z.), and Richmond (L. B.). -- Submaps of maps. I. General 0-1 laws. Journal of Combinatorial Theory. Series B, vol. 55, n°1, 1992, pp. 104--117.
[4]: Bender (E. A.), Gao (Z.), and Richmond (L. B.). -- Almost all rooted maps have large representativity. Journal of Graph Theory, vol. 18, n°6, 1994, pp. 545--555.
[5]: Bender (E. A.), Gao (Z.), Richmond (L. B.), and Wormald (N. C.). -- Asymptotic properties of rooted 3-connected maps on surfaces. Australian Mathematical Society. Journal. Series A. Pure Mathematics and Statistics, vol. 60, n°1, 1996, pp. 31--41.
[6]: Bender (E. A.) and Richmond (L. B.). -- Submaps of maps. III. k-connected nonplanar maps. Journal of Combinatorial Theory. Series B, vol. 55, n°1, 1992, pp. 125--132.
[7]: Gao (Z.). -- A pattern for the asymptotic number of rooted maps on surfaces. Journal of Combinatorial Theory. Series A, vol. 64, n°2, 1993, pp. 246--264.
[8]: Richmond (L. B.) and Wormald (N. C.). -- Almost all maps are asymmetric. Journal of Combinatorial Theory. Series B, vol. 63, n°1, 1995, pp. 1--7.
[9]: Tutte (W. T.). -- Graph theory. -- Addison-Wesley Publishing Co., Reading, Mass., 1984, Encyclopedia of Mathematics and its Applications, vol. 21, xxi+333p. With a foreword by C. St. J. A. Nash-Williams.

1: See also the summary on the same subject by Frédéric Chyzak in the 1995--1996 edition.

This document was translated from L^AT_EX by H^EV^EA.