From Motzkin to Catalan Permutations: a ``Discrete Continuity''

Renzo Pinzani

DSI, Università degli Studi di Firenze, Italy

Algorithms Seminar

March 2, 1998

[summary by Alain Denise]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).

Abstract
Let Sj be the set of all permutations with forbidden sequences 321 and (j+2)1_(j+3)2··· (j+1). We give the generating function of Sj according to three parameters: the length of the permutations, their number of right minima, and their number of inversions. The cases j=1 and j=2 give the generating functions of the well-known Motzkin numbers and left-Motzkin numbers, while the case j=¥ leads to the Catalan numbers. This is joint work with E. Barcucci, A. Del Lungo and E. Pergola.



1   Notations and Definitions

Definition 1   Let Sn be the set of permutations of [ n] . A permutation p Î Sn is said to contain a subsequence of type t Î Sk if there exists a sequence of indices 1£ it (1) <it (2) <...<it (k) £ n such that p (i1) <p (i2) <...<p (ik). We denote the set of permutations of Sn not containing subsequences of type t by Sn(t ) .

Example 1   The permutation 6145732 belongs to S7(2413) because all its subsequences of length 4 are not of type 2413. This permutation does not belong to S7(3142) because there exist subsequences of type 3142: p(1) p(2) p(5) p(6)=6173, p(1) p(2) p(5) p(7)=6172.

Definition 2   A barred permutation of [ k] is a permutation of Sk having a bar over one of its elements. If t_ is a barred permutation, we note t the permutation on [ k] identical to t_ but unbarred, and t^ the permutation of [ k-1] made up of the k-1 unbarred elements of t_, rearranged to get a permutation on [ k-1] .

Definition 3   We say that a permutation p Î Sn contains a type t_ subsequence if p contains a type t^ subsequence that, in turn, is not a type t subsequence. We denote the set of permutations of Sn not containing type t_ subsequences by Sn( t_) .

Example 2   If t_=41 3_ 52, then t =41352 and t^=3142 . The permutation p =6145732 belongs to S 7(t_) because all its subsequences of type t^: p(1) p(2) p(5) p(6) =6173, and p(1) p(2) p(5) p(7) =6172 are subsequences of p(1) p(2) p(3) p(5) p(6) =61473 and p(1) p(2) p (3) p(5) p(7) =61472, which are of type t.

Given some barred of unbarred permutations t 1Î Sk1,...,t pÎ Skp of, we denote the set Sn(t 1) Ç ...Ç Sn(t p) by Sn(t 1,...,t p) . We call the family F={ t 1,...,t p} a family of forbidden subsequences, the set Sn( F) a family of permutations with forbidden subsequences.

Example 3   The permutation p =6145732 belongs to S7(2413,41 3_ 52).

Let p Î Sn. We denote the position lying on the left of p(1) by s0, the position lying between p(i),p(i+1), 1 £ i £ n-1, by si and the position lying on the right of p(n) by sn. These positions s0,s1,...,sn-1,sn are called the sites of p.

Definition 4   Let F={ t 1,...,t p} . A site si (0 £ i £ n) of a permutation p Î Sn(F) is said to be active if the insertion of (n+1) into si gives a permutation belonging to the set Sn+1(F) ; otherwise the site is said to be inactive.

Definition 5   Let p Î Sn. The pair (i,j) is an inversion if p (i) >p (j). An element p (i ) is a right minimum if p (i) <p (j), " jÎ [ i+1,n] .

Example 4   The permutation p =6145732 has twelve inversions:
(1,2)(1,3)(1,4)(1,6)(1,7)(3,6)(3,7)(4,6)(4,7)(5,6)(5,7)(6,7)
and two right minima: p (2 )=1 and p (7 )=2.

2   Succession Rules and Generating Trees

In this section we briefly describe the tools used to deduce our enumerative results, that is succession rules and generating trees; they were introduced in [1] for the study of Baxter permutations and further applied to the study of permutations with forbidden subsequences by others (see [2] for example).
Definition 6   A generating tree is a rooted, labeled tree having the property that the labels of the set of children of each node v can be determined from the label of v itself. Thus, any particular generating tree can be specified by a recursive definition consisting in:
  1. the basis: the label of the root,
  2. the inductive step: a set of succession rules that yield a multi-set of labeled children depending solely on the label of the parent.
A succession rule contains at least the information about the number of children. Let t be a forbidden subsequence. Following the idea developed in [1], the generating tree for t-avoiding permutations is a rooted tree such that the nodes on level n are exactly the elements of Sn(t); the children of a permutation p=p(1)···p(n) are all the t free permutations obtained by inserting (n+1) into p. Labels must be assigned to the nodes and they record the number of children of a given node.

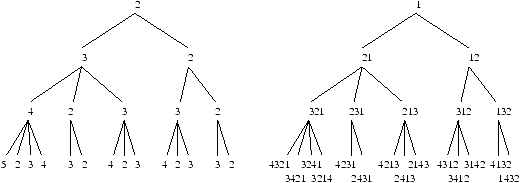
Example 5  [Catalan tree and 123-avoiding permutations]  
ì
í
î
basis:   (2)
inductive step:   (k) ® (k+1)(2)···(k).
The permutation of length one has two active sites (basis). Let p=p(1)···p(n) Î Sn(123); and k, 2 £ k £ n, be the minimum index in p such that i1 < k exists and p(i1) < p(k); then the active sites of p are s0,...,sk-1. The insertion of (n+1) into each other site on the right of sk-1 gives the subsequence p(i1) p(k) (n+1) that is forbidden. This means that the active sites of p are all the ones lying between the elements of p constituting the longest initial decreasing subsequence. If p has k active sites then its longest initial decreasing subsequence has length (k-1). The permutation obtained by inserting (n+1) into s0 give a new permutation with (k+1) active sites; the permutation obtained by inserting (n+1) into si, 1 £ i £ k-1, gives (i+1) active sites, (inductive step). The generating tree representing 123-avoiding permutations can be obtained by developing the above rule and by labelling each permutation with the right label (k) (see figure 1).


Figure 1: The generating tree of 123-avoiding permutations. (Left: nodes labelled by the numbers of active sites. Right: nodes labelled by the permutations.)

Example 6  [Schröder tree and (1234,2134)-avoiding permutations]  
ì
í
î
basis:   (2)
inductive step:   (k)® (k+1)(k+1)(3)···(k).
The permutation of length one has two active sites (basis). Let p=p(1)···p(n) Î Sn(1234,2134) and k, 3 £ k £ n, be the minimum index in p such that there exist i1<i2 < k for which p(i1) p(i2) p(k) is of type 123, or 213; then the active sites of p are s0,...,sk-1. The insertion of (n+1) into each other site sk,...,sn gives at least one of the forbidden subsequences 1234, 2134. Let p be a permutation with k active sites; the permutations obtained by inserting (n+1) into s0 and s1 have (k+1) active sites; the permutation obtained by inserting (n+1) into si, 2 £ i £ k-1, has (i+1) active sites; each other site gives at least one of the two forbidden subsequences because (n+1) has at least two smaller elements on its left (inductive step).

3   Permutations with one Forbidden Subsequence of Increasing Length

Let
Sj =
 
È
n ³ 1
Sn(321,(j+2)
_
1
 
(j+3)2···(j+1)).
Given a permutation p Î Sj, we denote its length by n(p), the number of its right minima by m(p), the number of its inversions by i(p). The generating function of Sj according to the above mentioned parameters is the following:
Sj(x,y,q)=
 
å
p Î Sj
x
n(p)
 
y
m(p)
 
q
i(p)
 
.

Note that the permutation of length one has two active sites and a permutation p having k active sites gives k permutations with (k)···(j)(j)···(2)(k+1) active sites respectively so the rule that describe the active sites changes has the form:
ì
í
î
(2)
(k) ® (k-1)···(j)(j)···(2)(k+1).

Now we can present our main result concerning the generating series Sj(x,y,q). One can observe (for example by setting j=1, 2, 3,... and then j=¥ in Sj(x,1,1), or by means of bijections with other combinatorial structures), that the classes of permutations described here are enumerated by numbers lying between the Motzkin and the Catalan numbers (see figure 1). We view the obtained sequences of numbers as providing a ``discrete continuity'' between the Motzkin and the Catalan sequences.

Theorem 1   The generating function of Sj(x,y,q) is such that:
S2(x,y,q)
=
xy(1+f(x,y,q))
1-xq-xq(1+q)f(x,y,q)
;     with   f(x,y,q)= y
 
å
n ³ 0
(-1)n xn+1 qn(j+1)
(xy,q)n+1 (q,q)n
 
å
n ³ 0
(-1)n xn qn(j+1)
(xy,q)n (q,q)n
,
Sj(x,y,q)
=
xy(1-xq2) D j(x,y,q)
(1-xq)(1-xq2) D j(x,y,q)+xy Dj-1(x,y,q)
,      j ³ 3,
where (a,q)n= Õk=0n-1 (1-aqk ), and with Dj(x,y,q)= c1(x,y,q) l1j(x,y,q)+ c2(x,y,q) l2j(x,y,q) where
l1(x,y,q)
=
1
2
é
ê
ê
ê
ê
ê
ë		 - æ
ç
ç
è		 1+
xy
1-xq2
ö
÷
÷
ø		 + ( æ
ç
ç
è		 1+
xy
1-xq2
ö
÷
÷
ø
2



 
-
4xy
( 1-xq2 ) ( 1-xq3 )
)1/2  ù
ú
ú
ú
ú
ú
û		 ,
l 2(x,y,q)
=
1
2
é
ê
ê
ê
ê
ê
ë		 - æ
ç
ç
è		 1+
xy
1-xq2
ö
÷
÷
ø		 - ( æ
ç
ç
è		 1+
xy
1-xq2
ö
÷
÷
ø
2



 
-
4xy
( 1-xq2 ) ( 1-xq3 )
)1/2  ù
ú
ú
ú
ú
ú
û		 .
The functions c1(x,y,q),c2(x,y,q) satisfy:
c1(x,y,q)l12(x,y,q)+c2(x,y,q) l22(x,y,q) =1+f(x,y,q)
c1(x,y,q) l13(x,y,q)+c2(x,y,q) l23(x,y,q)
=f(x,y,q)
xqj-1(1+q)-xy
1-xqj-1
-
1+xy-xqj-1
1-xqj-1
.

Index Rule Family of permutations First coeffs.
j=1 {
(2)
(k) ® (k-1) ··· (1) (k+1)
.		 Sn1(321,31_42) 1,2,4,9,21,...
j=2 {
(2)
(k) ® (k-1) ··· (2) (2) (k+1)
.		 Sn2(321,41_523) 1,2,5,13,35,...
j=3 {
(2)
(k) ® (k-1) ··· (3) (3) (2) (k+1)
.		 Sn3(321,51_6234) 1,2,5,14,41,...
j {
(2)
(k) ® (k-1) ··· (j) (j) ··· (2) (k+1)
.
Snj(321,(j+2)
_
1
 
(j+3)
  23···(j+1))
1,2,5,14,42,...
j=¥ {
(2)
(k) ® (k) ··· (2) (k+1)
.		 Sn¥(321) 1,2,5,14,42,...



Table 1: A few permutations of Sj.

References

[1]
Chung (F. R. K.), Graham (R. L.), Hoggatt, V. E. (Jr.), and Kleiman (M.). -- The number of Baxter permutations. Journal of Combinatorial Theory. Series A, vol. 24, n°3, 1978, pp. 382--394.

[2]
West (Julian). -- Generating trees and forbidden subsequences. Discrete Mathematics, vol. 157, n°1-3, 1996, pp. 363--374. -- Proceedings of the 6th Conference on Formal Power Series and Algebraic Combinatorics (New Brunswick, NJ, 1994).
This document was translated from LATEX by HEVEA.