Dynamical Systems and Average-Case Analysis of General Tries
Brigitte Vallée
GREYC, Université de Caen, France
Algorithms Seminar
June 9, 1997
[summary by Julien Clément]
A properly typeset version of this document is available in
postscript and in
pdf.
If some fonts do not look right on your screen, this might be
fixed by configuring your browser (see the documentation here).
Abstract
The three major parameters of a trie
(sometimes called digital tree),
number of nodes, path length, and height,
are analyzed precisely in a general context where words are emitted
by a source associated to a dynamical system.
The results can all be stated in terms of two intrinsic characteristics
of the source: the entropy and the probability of letter coincidence.
These characteristics themselves are linked in a natural way
to spectral properties of a Ruelle operator associated to the
dynamical system.
1 Probabilistic dynamical sources
1.1 Definitions
A dynamical source, in the context of information theory, is a
mechanism which produces infinite words over an alphabet M.
Such a system is defined by four elements:
(i) an alphabet M included in N,
(ii) a quasi partition of I=]0,1[
with intervals Im, m Î M,
(iii) a mapping s: I ® M which is
constant over each Im and equal to m and finally
(iv) a mapping T: I ® I
which satisfies two properties: the restriction
of T to Im is a real analytic bijection from
Im to I; the mapping T is expansive,
i.e. |T'(x)|>1 on I.
The words emitted by the source are produced by iterating T and
coded thanks to s.
The word M(x)
of M¥ (an infinite sequence of symbols), where
xÎ I, is formed with the symbols
M(x):=(s(x),s(T(x)),s(T2(x)),...,s(Tk(x)),...).
Each letter of the alphabet is associated to a distinct
branch of T or equivalently to a distinct inverse branch of T
denoted by hm. The bijection hm: I ® Im
coincides with the inverse of the restriction
of T to Im.
1.2 Examples
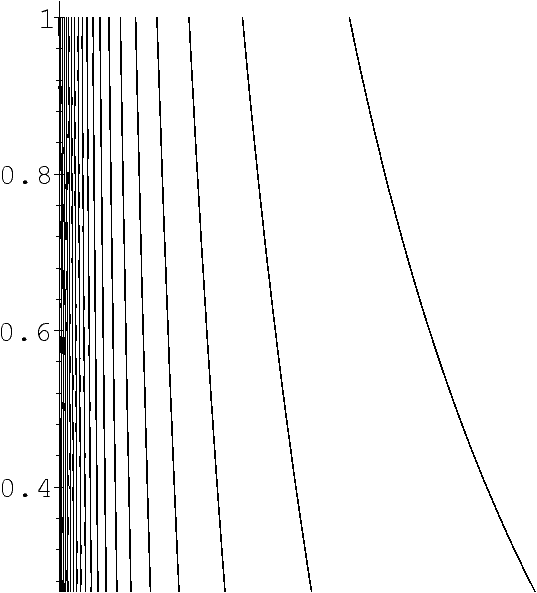
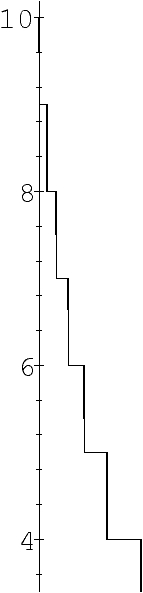
Figure 1: Graphical representation of the mappings T and
s for a source based on the continued fraction expansion
(left) and
for a memoryless source based on the 5-ary expansion of numbers (right).
A lot of probabilistic dynamical sources can be described in such a
framework, including all memoryless sources where letters of the
alphabet can be emitted with probabilities {pi} independently of
previous letters. This gives a mapping T where branches are
affine. In particular this encompasses the b-ary expansion model of
numbers.
Markov sources take into account a finite past for producing
words and thus generalize memoryless sources.
Finally, in a model where the source is based upon the continued
fraction expansion of
numbers, the alphabet is N and the probability for a character to
be emitted depends on all the previous history.
1.3 Fundamental intervals, entropy, coincidence probability
Numbers which share the same prefix expansion m1,...,mk form an
interval called fundamental interval of depth k which is exactly,
with the preceding notations,
In a general context, the
interval I is endowed with a continuous density f (so
that F
denotes the associated distribution).
Then the word M(x) is produced
according to the expansion process (using T and s).
In this context, the measure uh of a fundamental interval
Ih
associated to h=hm1 ° ... ° hmk is
uh:= |F(h(0))-F(h(1))|,
and plays a crucial role since it is the probability that a word
begins with a certain prefix.
During the analysis, two quantities relative to the source appear
naturally.
The entropy h( S,F) and the coincidence probability
c( S,F) are defined as
the limits
| h( S |
,F):=
|
|
|
|
|
|
uh log uh,
c( S |
,F):=
|
|
|
|
1/k.
|
2 Tries associated to a general source
Let M Î N be a set of elements called digits, and
M¥ the set of all infinite sequences built over
M.
For any word produced by the dynamical source
M(x)=(s(x),s(Tx),s(T2x),...) (with x Î I),
the head and tail
functions are defined by
head(M(x))=s(x), tail(M(x))=M(Tx).
Any finite set of infinite words produced by the same source can be
written as M(X)={M(x) |x Î X}, and one associates to X a
trie, Trie(X), defined by the following recursive rules
-
(R1) If X={x} has cardinality equal to 1, then Trie(X)
consists of a single leaf node that contains M(x).
- (R2) If X has cardinality at least 2, then Trie(X)
is an
internal node represented generically by `o' to which are attached
l subtrees, where
l=card{s(x) |x Î X} is the number
of different head symbols in M(X). Let b1<...< bl be these
head symbols; Trie(X) is defined by
| Trie(X)=á o,Trie(X1),...,Trie |
(X |
|
)ñ,
where
Xj={Tx| s(x)=bj, x Î X}. |
2.1 Parameters
The main parameters of a trie
are size (number of internal nodes), height and external
length path, which is the sum of all links from the root to each leaf.
The model considers here infinite strings emitted independently by the
same dynamical source.
Rather than considering a fixed number n of strings,
a Poisson model of rate n is used, where the number of strings N is also a
random variable which strongly concentrates around n.
The strong property
of independence of this particular model makes the analysis easier and
gives access to the expectations of parameters.
The expectations of height, size and external path length under a
Poisson model of rate n and distribution F over I are
respectively
| D(n)= |
|
[1- |
|
(1+nuh)e |
|
],
S(n)= |
|
[1-(1+n uh) e |
|
],
P(n)= |
|
n uh [1-e |
|
]. |
2.2 Asymptotics
These quantities are easily recognized as harmonic sums of the form
F(x)=åk Î K lk f(µk x) (excepted for the height
which needs a small calculation step before).
The best tool to analyze
the asymptotics of
such harmonic sums is the Mellin transform, which leads to
locating poles of the associated Dirichlet series
L(s)=åk Î K lk µks.
Here, the key quantity for the analysis of size and path length is the
series of fundamental intervals,
| L(F,s)= |
|
uhs= |
|
|F(h(0))-F(h(1))|s, |
3 Generalized Ruelle operators
3.1 Presentation
The generalized Ruelle operators are derived from the original Ruelle
operators, and involve secants of the inverse branches
H(u,v):=|(h(u)-h(v))/(u-v)|.
The generalized Ruelle operators are defined by
| G |
s[F](u,v)= |
|
|
|
(u,v)s F(h(u),h(s)), |
| L(F,s)= |
|
uhs= |
|
|F(h(0))-F(h(1))|s=
(I-Gs)-1[Ls](0,1). |
3.2 Singularities of the quasi inverse (I-Gs)-1
Singularities of (I-Gs)-1 are of special
interest because these are also singularities of L(F,s).
These singularities arise for values of s where Gs has
an eigenvalue equal to 1. In particular, there is always a pole at
s=1 (easy to prove from the previous form of L(F,s)).
One can derive from strong properties of the operator
Gs that there are three different cases,
called periodic, quasi-periodic and aperiodic,
depending on the precise nature of the eigenvalues of Gs
on the line Â(s)=1.
The operator Gs has also special properties at s=1 and s=2
since the entropy of the
source is h( S)=-l'(1)
(the derivative of the dominant eigenvalue at
s=1), while the coincidence probability is c( S)=l(2).
4 Average-case analysis of general tries
4.1 Analysis of height
The analysis of height is based on estimates of the individual
probabilities pk(n)=Õ|h|=k (1+n uh) e-n uh
followed by a Mellin analysis.
This leads to the asymptotic expansion
| D(n)=
|
|
log n +PF(log n)+
g+AF+o(1) |
4.2 Analysis of size and path length
The operator (I-Gs)-1 has a simple pole at s=1, and
thus gives the main term of the asymptotic expansion. For a general
source, a Tauberian theorem can be applied to estimate the
contribution of others poles.
Finally one has
| P(n)= |
|
n log n + o(n log n),
S(n)= |
|
n + o(n). |
5 Some important particular cases
5.1 Bernoulli sources
The Bernoulli source considers a finite alphabet M={1,..., r} with probability of emission {p1,...,pr}
(with p1+...+pr=1). In this case the entropy and the
coincidence probability have classical expressions
5.2 Continued fraction source
The continued fraction expansion of numbers can be considered as a
dynamical source over the infinite alphabet M=N. The operator of Ruelle is then
called the Ruelle-Mayer operator and
is defined by
The entropy of the source is linked to the so-called
Lévy's constant which plays a central rôle in the the analysis of
the Euclidean algorithm. The coincidence probability is a constant
which intervenes in two-dimensional generalizations of the Euclidean
algorithm.
These constants are
References
- [1]
-
Brigitte Vallée. --
Dynamical systems and average-case analysis of general tries. --
Les cahiers du GREYC, 1997.
- [2]
-
Flajolet (Philippe) and Vallée (Brigitte). --
Continued Fraction Algorithms, Functional Operators, and
Structure Constants. --
Research Report n°2931, Institut National de Recherche en
Informatique et en Automatique, July 1996. 33 pages. Invited
lecture at the 7th Fibonacci Conference, Graz, July 1996; to appear in Theoretical Computer Science.
- [3]
-
Hervé Daudé (Philippe Flajolet) and Vallée (Brigitte). --
An Average-case Analysis of the Gaussian Algorithm for Lattice
Reduction. --
Research Report n°2798, Institut National de Recherche en
Informatique et en Automatique, February 1996. To appear in
Combinatorics, Probability and Computing, 1997.
- [4]
-
Jacquet (Philippe) and Szpankowski (Wojciech). --
Analysis of digital tries whith Markovian dependency. IEEE
Transactions on Information Theory, vol. 37, n°5, September
1991, pp. 1470--1475.
- [5]
-
Vallée (Brigitte). --
Opérateurs de Ruelle-Mayer généralisés et analyse en
moyenne des algorithmes d'Euclide et de Gauss. Acta Arithmetica,
vol. LXXXI, n°2, 1997, pp. 101--144.
This document was translated from LATEX by
HEVEA.