Eulerian Calculus: a Technology for Computer Algebra and Combinatorics

Dominique Foata

Département de mathématique, Université Louis Pasteur (France)

Algorithms Seminar

May 21, 2001

[summary by Dominique Gouyou-Beauchamps]

A properly typeset version of this document is available in postscript and in pdf.

If some fonts do not look right on your screen, this might be fixed by configuring your browser (see the documentation here).
Abstract
Babson and Steingrímsson have introduced pairs of permutation statistics that they conjectured were all Euler--Mahonian, i.e., equidistributed with the pair (des,maj) where des is the number of descents and maj is the major index. How to prove their conjecture? We use the so-called ``Umbral Transfer Matrix Method'' implemented by Zeilberger and specific combinatorial constructions leading to new transformations on the symmetric group. Details may be found in the recent work of D. Foata and D. Zeilberger [2].



1  Introduction

We use the Babson--Steingrímsson notation [1] for ``atomic'' permutation statistics. Given a permutation w=x1x2... xn of 1, 2, ..., n they denote (a-bc)(w) the number of occurences of the pattern a-bc, i.e., the number of pairs of places 1£ i<j<n such that xi<xj<xj+1. Similary, the pattern (b-ca)(w) is the number of ocurrences of xj+1<xi<xj, and in general, for any permutation a, b, g of a, b, c, the expression (a-bg)(w) is the number of pairs (i,j), 1£ i<j<n, such that the orderings of the two triples (xi,xj,xj+1) and a,b,g are identical. The statistic (ab-c) is defined in the same way by looking at the occurences (xi,xi+1,xj) such that i+1<j and xi<xi+1<xj. Of course, (ba)(w) denotes the number des w of descents of w (i.e., the number of places 1£ i<n such that xi>xi+1) and (ab)(w) denotes the number rise w of rises of w (i.e., the number of places 1£ i<n such that xi<xi+1).

The classical permutation statistics inv and maj may be written as (bc-a)+(ca-b)+(cb-a)+(ba) and (a-cb)+(b-ca)+(c-ba)+(ba), respectively. This inspired Babson and Steingrímsson to perform a computer search for all statistics that could be thus written, and look for those that appear to be Mahonian. They came up with a list of 18. Some of them turned out to be well-known, and some were new. Yet eight new conjecturally Mahonian statistics were left open. Here we prove four of them.

2  Notations

Recall the usual notations
(a;q)n = ì
í
î
1 if n=0,
(1-a )(1-aq)... (1-aqn-1) if n³ 1,
(a;q)¥=
 
lim
n®¥
(a;q)n=
 
Õ
n³0
(1-aqn),
[n]q =
1-qn
1-q
=
n-1
å
i=0
qi,      [n]q! =
(q;q)n
(1-q)n
=
n
Õ
i=1
 [i]q.

A statistic stat on the symmetric group Sn is said to be Mahonian, if for every n³ 0 we have
 
å
wÎSn
qstat w = [n]q!

A sequence (An(t,q))n³ 0 of polynomials in two variables t and q, is said to be Euler--Mahonian, if one of the following equivalent conditions holds:
  1. For every n³ 0,
    1
    (t;q)n+1
    		An(t,q) =
     
    å
    s³ 0
    		ts([s+1]q)n.
  2. The exponential generating function for the fractions An(t,q)/(t;q)n+1 is given by
     
    å
    n³ 0
    un
    n!
    An(t,q)
    (t;q)n+1
    		=
     
    å
    s³ 0
    		ts exp(u[s+1]q).
  3. The sequence (An(t,q)) satisfies the recurrence relation:
    (1-q)An(t,q)=(1-tqn)An-1(t,q)-q(1-t)An-1(tq,q).     (1)
  4. Let An(t,q)=ås³ 0tsAn,s(q). Then the coefficients An,s(q) satisfy the recurrence:
    An,s(q) = [s+1]qAn-1,s(q)+qs[n-s]qAn-1,s-1(q).
Now a pair of statistics (stat1,stat2) defined on each symmetric group Sn (n³ 0) is said to be Euler--Mahonian, if for every n³ 0 we have
 
å
wÎSn
tstat1wqstat2w = An(t,q).

3  Results

Our results are the following:
Theorem 1   The permutation statistic S11=(a-cb)+2(b-ca)+(ba) is Mahonian.
Theorem 2   The permutation statistic S13=(a-cb)+2(b-ac)+(ab) is Mahonian.
Theorem 3   Let S5=(b-ca)+(c-ba)+(a-bc)+(ab). Then, the pair (rise,S5) is Euler--Mahonian.
Theorem 4   Let S6=(ba-c)+(c-ba)+(ac-b)+(ba). Then, the pair (des,S6) is Euler--Mahonian.
Our Theorems 1, 2, and 4 are the three parts of Conjecture 8 of [1], while Theorem 3 is Conjecture 10 of [1]. It turns out that, thanks to Zeilberger's recent theory of the Umbral Transfer Matrix Method [4], the proofs of the first three theorems are completely automatic, using the general Maple package ROTA, together with a new interfacing package PERCY that computes the appropriate Rota operators for what we will call Markovian Permutation Statistics.

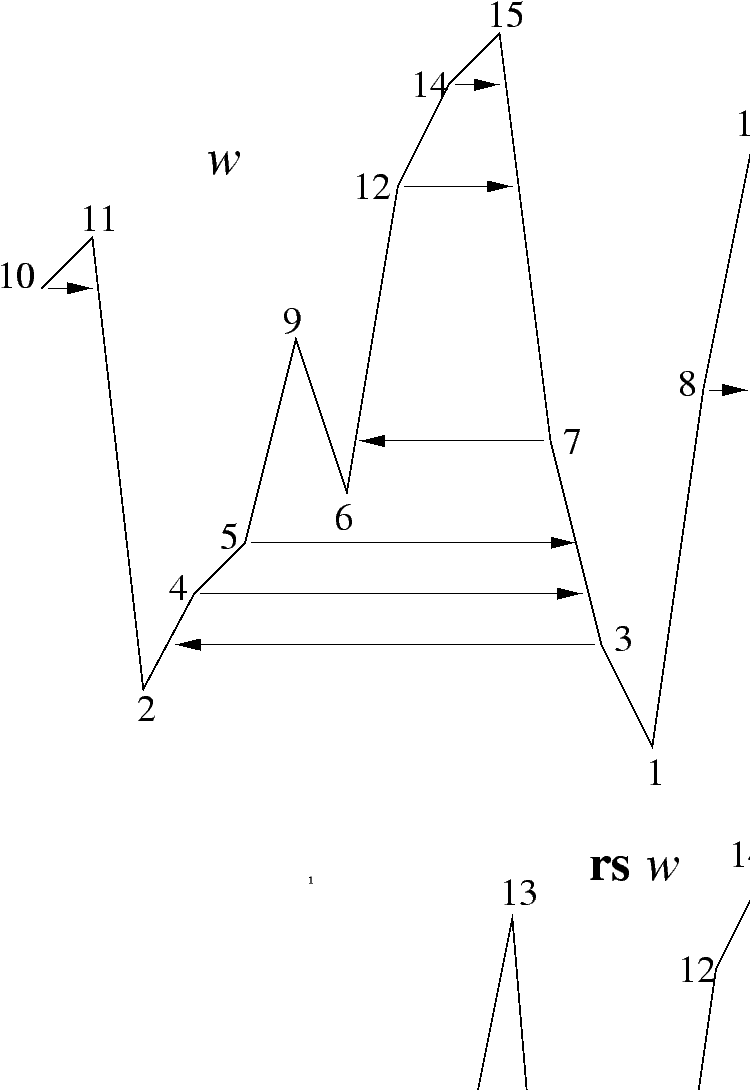
Figure 1: rs(10,11,2,4,5,9,6,12,14,15,7,3,1,8,13) = (8,13,1,4,5,12,14,15,7,6,9,3,2,10,11).

However, ROTA is useless in the case of S6. So proving Theorem 4 still requires the traditional combinatorial method: construct a bijection w|® w' of Sn onto itself which has the property that
(des,S6) w' = (des,maj) w
holds for every wÎSn.

4  Proof of Theorem 4

Instead of the pair (des,maj) we will take another Euler--Mahonian pair (des,mak), where mak is a Mahonian statistic that was introduced by Foata and Zeilberger in [3]. In the Babson--Steingrímsson notation mak reads
mak := (a-cb)+(cb-a)+(ba)+(ca-b).

First, the descent bottom of a permutation x1x2... xn is defined to be the set desbot w of all the xi's such that 2£ i£ n and xi-1>xi. Its cardinality is the number des w of descents of w.

Next, the word statistics U and V are introduced as follows. Let y=xi be a letter of the permutation w=x1x2... xn. Define
Uy(w) = (ca-b) | b=yw;      Vy(w) = (b-ac) | b=yw.
Thus, Uy(w) is the number of adjacent letters xjxj+1 to the left of y=xi such that xj>xi>xj+1. The word statitics U and V are then:
U(w)=U1(w)U2(w)... Un(w);     V(w)=V1(w)V2(w)... Vn(w).

Now, recall the traditional reverse image r, which is an involution that maps each permutation w=x1x2... xn onto r w=xnxn-1... x1. We shall introduce another involution s of Sn, called the rise-des-exchange, which exchanges the rises and the descents of a permutation and keeps peaks and troughs in their original ordering. The involution s is not explained here, but can be immediately visualized in Fig. 1.
Proposition 1   The involution rs of Sn has the following properties:
  1. desbotrs w = desbot w,
  2. (U,V) rs w = (V,U) w.

Let S-desbot w be the sum of all the letters xi of the permutation w=x1x2... xn which belong to the descent bottom set desbot w.
Proposition 2   For each permutation w we have:
S-desbot w = ( (a-cb)+(cb-a)+(ba) )  w.

Next, we introduce the complement to (n+1), denoted by c, that maps each permutation w=x1x2... xn onto c w = (n+1-x1)(n+1-x2)... (n+1-xn). Thus the statistic S6 rc reads
S6 rc = (a-cb)+(cb-a)+(ba)+(b-ca) .
Taking Proposition 2 into account, we get the expressions:
mak w = S-desbot w+U1(w)+... +Un(w),
S6 rc = S-desbot w+V1(w)+... +Vn(w).

Therefore, Proposition 1 implies the following corollary.
Corollary 1   The involution rs is an involution of Sn having the property:
(des,mak) w = (des,S6 rc) rs w.

But (des,mak) is Euler--Mahonian, as proved in [3]. Therefore, the pair (des, S6 rc) is Euler--Mahonian, as well as (des,S6), since we always have desrc w = des w. Hence Theorem 4 is proved.

5  Markovian Permutation Statistics

The reduction of a sequence w of n distinct integers, denoted by red(w), is the permutation obtained by replacing the smallest member by 1, the second-smallest by 2, ..., and the largest by n. For example red(5 8 3 7 4) = 3 5 1 4 2.

A permutation statistic F:Sn®Z is said to be Markovian, if there exists a function h(j,i,n) such that
F(x1... xn) = F ( red(x1... xn-1) ) +h(xn-1,xn,n).
A Markovian permutation statistic F:Sn®Z is said to be nice Markovian if the above h(j,i,n) can be written as
h(j,i,n) = ì
í
î
f(j,i,n) if j<i,
g(j,i,n) if j>i,
where f and g are affine linear functions of their arguments, i.e., can be written as ai+bj+cn+d, for some integers a, b, c, d.

We, and the Maple package PERCY, will only consider nice Markovian statistics. We will denote them by [f,g,j,i,n]. For exemple, inv = [n-i,n-i,j,i,n], maj = [0,n-1,j,i,n], des = [0,1,j,i,n], rise = [1,0,j,i,n].

Given a permutation statistic F we are interested in the sequence of polynomials
gf (F)n(q) =
 
å
wÎSn
qF(w)    (n³ 0).
However, in order to take advantage of Markovity, we need to consider the more refined
GF (F)n(q,z) =
 
å
w=x1... xnÎSn
qF(w) zxn    (n³ 0)
that also keeps track of the last letter xn. Now, by using Rota operators [4], it is easy to express GF(F)n in terms of GF(F)n-1. Let w'=x'1... x'n-1=red(x1... xn-1); then
GF(F)n(q,z) =
n
å
i=1
zi
 
å
wÎSn; xn=i
qF(w)
  =
n-1
å
j=1
 
å
w'ÎSn-1; x'n-1=j
æ
ç
ç
è
j
å
i=1
qg(j+1,i,n)zi+
n
å
i=j+1
qf(j,i,n)zi ö
÷
÷
ø		 qF(w').

Now for i£ j£ n-1 we introduce the umbra P,
P(zj) = æ
ç
ç
è
j
å
i=1
qg(j+1,i,n)zi+
n
å
i=j+1
qf(j,i,n)zi ö
÷
÷
ø		 ,
and we extend by linearity, so that P is defined on all polynomials of degree less than or equal to n-1. In terms of P, we have the very simple recurrence:
GF(F)n(q,z) = P ( GF(F)n-1(q,z) ) .
Maple can compute the umbra automatically. All the users have to enter is f and g, and PERCY would convert it to the Markovian notation.

6  Proof of Theorem 1

Using PERCY and ROTA we get that the umbra P linking GF(S11)n-1(q,z) to GF(S11)n(q,z) maps the polynomial a(z) onto
zn+1a(1)-za(z)
z-1
+
z ( a(qz)-a(q2) )
z-q
.
Hence bn(z)=GF(S11)n(q,z) satisfies the functional recurrence
bn(z) =
zn+1bn-1(1)-zbn-1(z)
z-1
+
z ( bn-1(qz) -bn-1(q2) )
z-q
,
with the initial condition b1(z)=z. But if we guess (and if we check) that the sequence
cn(z)=z
zn-qn
z-q
[n-1]q!
satisfies the same recurrence, we obtain that bn(z)=cn(z), and finally that bn(1)=cn(1)=[n]q!

7  Proof of Theorem 2

Using PERCY and ROTA we get that the umbra P linking GF(S13)n-1(q,z) to GF(S13)n(q,z) maps the polynomial a(z) onto
z ( a(zq)-a(1) )
qz-1
+
zqa(z)-q2n+1zn+1a(q-2)
1-zq2
.
Hence dn(z)=GF(S13)n(q,z) satisfies the functional recurrence
dn(z) =
z ( dn-1(zq)-dn-1(1) )
qz-1
+
zqdn-1(z) -q2n+1zn+1dn-1(q-2)
1-zq2
,
with the initial condition d1(z)=z. But if we guess (and if we check) that the sequence
en(z)=z
(1-znqn)
1-qz
[n-1]q!
satisfies the same recurrence, we obtain that dn(z)=en(z), and finally that dn(1)=en(1)=[n]q!.

8  Proof of Theorem 3

PERCY can compute the Umbra multi-statistics, when the generating function is the weight-enumerator of Sn according to the weight
weight (w) = zxn
r
Õ
j=1
qjFj(w),
where w=x1... xn and F1(w), ..., Fr(w) are several nice Markovian permutation statistics. Define
An(t,q;z)=
 
å
wÎSn
tdes wqmaj wzxn,      Bn(t,q;z)=
 
å
wÎSn
trise wqS5wzxn.
PERCY and ROTA compute the following functional recurrences
  An(t,q;z) =
z(1-tqn-1)An-1(t,q;z)-z(zn-tqn-1)An-1 (t,q;1)
1-z
;
    (2)
Bn(t,q;z)=
z(1-tqn)Bn-1(t,q;z)-z(1-tzn)Bn-1(t,q;q)
z-q
.
By comparing the two functional recurrences, we guess and we verify that
Bn(t,q;z)=q-nzn+1An(tq,q;q/z).
Hence Bn(t,q;1)=q-nAn(tq,q;q). By plugging t=tq, z=q into Eq. (2), we get that
An(tq,q;q) = qn
(1-tqn)An-1(t,q;1)-q(1-t)An-1(tq,q;1)
1-q
.
But, this equals qnAn(t,q) by Eq. (1). And we have proved that Bn(t,q;1)=An(t,q;1)=An(t,q).

The input and output files of PERCY can be downloaded from
http://www.math.temple.edu/~zeilberg/programs.html.

References

[1]
Babson (Eric) and Steingrímsson (Einar). -- Generalized permutation patterns and a classification of the Mahonian statistics. Séminaire Lotharingien de Combinatoire, vol. 44, n°B44b, 2000. -- 18 pages. Available from http://www.mat.univie.ac.at/~slc/.

[2]
Foata (D.) and Zeilberger (D.). -- Babson-Steingrímsson statistics are indeed Mahonian (and sometimes even Euler-Mahonian). -- To appear in Advances in Applied Mathematics.

[3]
Foata (Dominique) and Zeilberger (Doron). -- Denert's permutation statistic is indeed Euler-Mahonian. Studies in Applied Mathematics, vol. 83, n°1, 1990, pp. 31--59.

[4]
Zeilberger (Doron). -- The umbral transfer-matrix method. I. Foundations. Journal of Combinatorial Theory. Series A, vol. 91, n°1-2, 2000, pp. 451--463. -- In memory of Gian-Carlo Rota.
This document was translated from LATEX by HEVEA.