
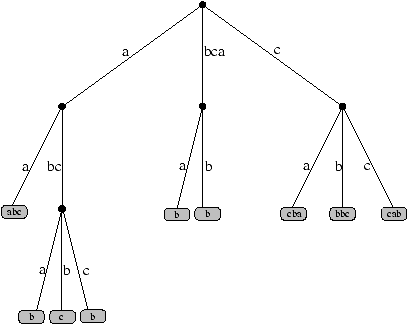
Figure 1: Standard trie and corresponding Patricia trie.
Tries, a generalized form of digital trees, are a data structure widely used in numerous domains: algorithms for searching words, compression, dynamical hashing, ... Their interest and construction lie in the partitioning of a set of words. We present a compact form of tries, called Patricia tries, in which all unary nodes are suppressed (and thus do not intervene in the partitioning). We then study the means of the memory occupation and of the cost of inserting a word for that data structure when words are produced by a probabilistic source for which the dependencies between the emitted symbols can be very important.
| Tr(X)= | ·, Tr |
æ è |
|
[a1]X |
ö ø |
, Tr |
æ è |
|
[a2]X |
ö ø |
,... Tr |
æ è |
|
[ar]X |
ö ø |
. |
Hence with any finite set X of infinite words produced by the same source, we associate a Patricia trie PaTr(X). The first two rules are the same, but the last rule (R'2) is more sophisticated:

Figure 1: Standard trie and corresponding Patricia trie.
| PaTr(X)= | ·, PaTr |
æ è |
|
[a1]X |
ö ø |
, PaTr |
æ è |
|
[a2]X |
ö ø |
,··· PaTr |
æ è |
|
[ar]X |
ö ø |
. |
|
|
[w]X:= |
æ è |
|
|
[w](x1),···, |
|
|
[w](xn) |
ö ø |
. |
| g[X]= |
|
| dS(s)= |
ì í î |
|
dPS(s)= |
ì í î |
|
| dL(s)= |
ì í î |
|
dPL(s)= |
ì í î |
|
Size of Tr S^(n)=åwÎS*( 1-(1+(n-1)pw)(1-pw)n-1 ) Path Length of Tr L^(n)=åwÎS*npw( 1-(1-pw)n-1 ) Size of PaTr SP^(n)=åwÎS*( 1-(1-pw)n-åiÎS( (1-pw(1-p[i|w]))n-(1-pw)n ) ) Path Length of PaTr LP^(n)=åwÎS*npw( 1-(1-pw)n-1-åiÎSp[i|w]( 1-pw(1-p[i|w]))n-1 )
Size of Tr S*(s)=-L(-s)(s+1)G(s) Path Length of Tr L*(s)=-L(-s)G(s+1) Size of PaTr SP*(s)=G(s)LS(-s) Path Length of PaTr LP*(s)=-G(s+1) (L(-s)+LL(-s))
Figure 2 displays several types of dynamical sources: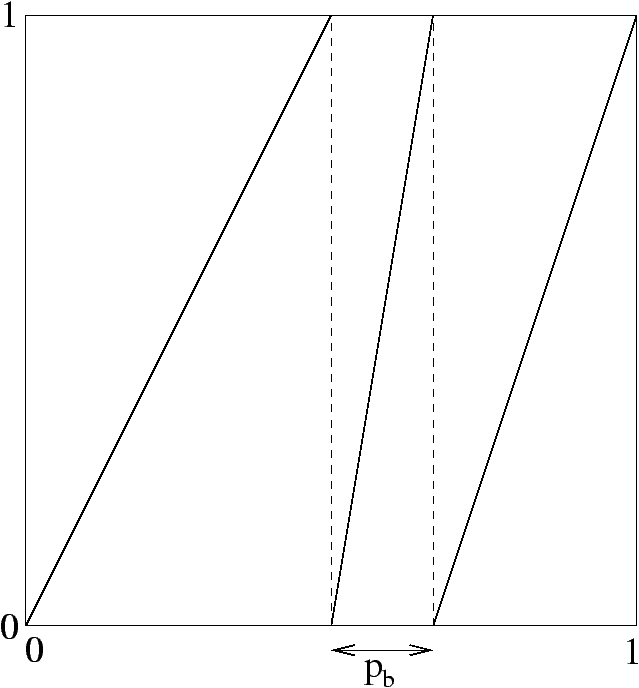
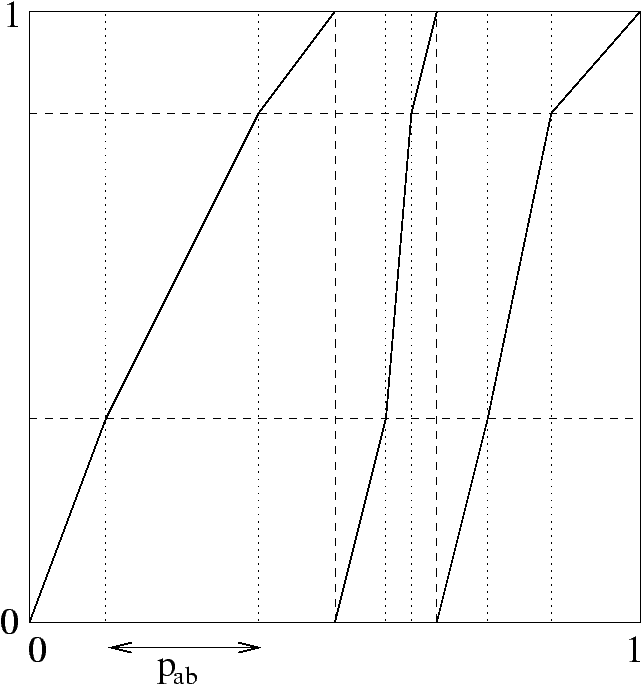
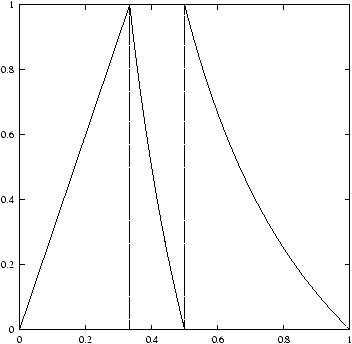
Figure 2: Memoryless source, Markov chain of order 1, continued fraction source, heteroclinal source.
| G | [f](x):= |
|
| | ha'(x) | | | f° ha(x), |
| G | s[f](x):= |
|
|
(x)s f° ha(x). |
| G | s[L](x):= |
|
|
s[ha](x,y) L | ( | ha(x),ha(y) | ) | . |
| G | s[m][L]:= |
|
Hs[m][ha] L° V[ha], |
| L(s)= |
|
pws=(Id-G | s)-1[Qs](0,1); L[k](s)= |
|
( | Id-Gs[k] | ) | -1 | [ | Hs[k][F] | ] | ( | 0,1,hi(0),hi(1) | ) | . |
| (Id-Gs)-1 = |
|
Ps+(Id-Ns)-1 ), |
|
(s-1)(Id-Gs)-1[L](x)= |
|
Y1(x) | ó õ |
|
l(t) dt), |
| L(s)=L[1](s)~ |
|
+C(S), |
| C1(S) | = |
|
|||||||||||||||||||||||||||||||||||||
| C2(S) | = |
|
Size of Tr S(n)»1/h(S)n Path Length of Tr L(n)~1/h(S)nlogn +(C(S)-g/h(S))n Size of PaTr SP(n)»1/h(S) (1-C1(S))n Path Length of PaTr L(n)~1/h(S)nlogn +(C(S)-g+C2(S)/h(S))n
| h(S) | = |
|
C(S) | = |
|
||||||||||||||||||||||||||||
| C1(S) | = |
|
C2(S) | = |
|
This document was translated from LATEX by HEVEA.