A PROBLEM IN STATISTICAL CLASSIFICATION THEORY

Philippe Flajolet

(Version of January 14, 1997)

This problem discussed here is at the origin of the whole Combstruct package. On October 8, 1992, Bernard Van Cutsem, a statistician at the University of Grenoble wrote to us:

In classification theory, we make use of hierarchical classification trees. I would need to generate at random such classification trees according to the uniform law. The elements to be classified may be taken as distinguished integers say from 1 to . Do you know of an algorithm for doing this?

This led to a cooperation involving Paul Zimmermann, Bernard Van Cutsem, and Philippe Flajolet, out of which the general theory and the algorithms of Combstruct evolved, see Theoretical Computer Science , vol. 132, pp. 1-35. A first implementation was designed by Paul Zimmermann in 1993, under the name Gaia ( Maple Technical Newsletter , 1994 (1), pp. 38-46).

Van Cutsem's original question was motivated by the following problem: Classification programmes in statistics build classification trees, usually proceeding by successive aggregations of closest neighbours amongst existing classes. How can we measure the way a classification carries useful information and not just "random noise"? Certainly, "good" classification trees should exhibit characteristics that depart significantly from random ones. Hence the need to simulate and analyse parameters of random classification trees.

Statistics and classification theory

Specification

We start by loading the combstruct package.

> with(combstruct);

A classification is either: 1) an atom; 2) a set of classification trees of degree at least 2. Atoms are distiguishable, hence we are in a labelled universe. Note that the Set construction translates a pure graph-theoretic structure with no ordering between descendents of a node.

> hier:=[H,{H=Union(Z,Set(H,card>1))},labelled]:

The original problem of Van Cutsem is solved by single commands like

> draw(hier,size=10);

We may adopt a more concise representation format:

> lreduce:=proc(e) eval(subs({Set=proc() {args} end, Sequence=proc() [args] end},e)) end:

> lreduce(draw(hier,size=20));

Random generation takes only a few seconds while counting tables (that serve to determine splitting probabilities) are set up on the fly.

> for j from 20 by 20 to 100 do j,lreduce(draw(hier,size=j)) od;

The number of objects of size grows fast

> seq(count(hier,size=j),j=0..40);

This appears to be sequence M3613 of the Encyclopedia of Integer Sequences and it corresponds to "Schroeder's fourth problem". When the count is not too large, we can do exhaustive listings. This is made possible by Combstruct that is able to build canonical forms and generate elements under unique standard forms.

> for j to 4 do map(lreduce,allstructs(hier,size=j)) od;

Asymptotic analysis

We get generating function equations by combstruct[gfeqns]

> gfeqns(op(2..3,hier),z);

And combstruct[gfsolve] attempts different strategies to solve the system

> gfsolve(op(2..3,hier),z);

The solution involves Lambert's W function that is known to Maple: by definition, this is the solution of

.

> H_z:=subs(",H(z));

Objects being labelled, this is an exponential generating function (EGF).

> H_ztayl:=series(H_z,z=0,20);

As usual, we also obtain the corresponding ordinary generating functions by a Laplace transform applied to the series expansion

> series(subs(w=1/w,w*inttrans[laplace](H_ztayl,z,w)),w,20);

The result is then directly comparable to the counting coefficients:

> seq(count(hier,size=j),j=1..18);

In order to analyse the number of hierarchies, we must find the dominant singularity of their generating function. A plot detects a vertical slope near 0.4

> plot(H_z,z=0..1);

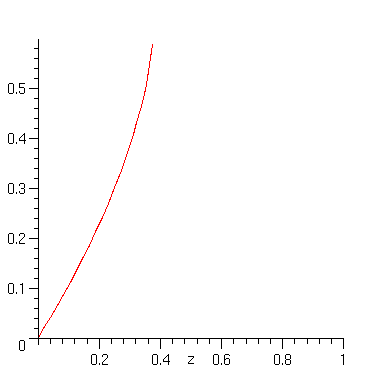
Here is a cute way to get the singularity "automatically". We express that the function ceases to be differentiable at its singularity.

> diff(H_z,z);

> rho:=solve(denom(")=0); evalf(rho,30);

Next, we know that the singular expansion determines the asymptotic form of coefficients. Thus, we look at

> H_s:=subs(z=rho*(1-Delta^2),H_z);

> H_sing:=map(simplify,series(H_s,Delta=0,5));Delta=sqrt(``(1-z/rho));

With this, we can get an asymptotic expansion for coefficients to any order, which is an interesting fact per se. Here is the first one:

> H_n_asympt:=n!*asympt(coeff(H_sing,Delta,1)*rho^(-n)*subs({cos(Pi*n)=1,O=0},simplify(asympt(binomial(1/2,n),n,2))),n);
evalf(",20);

And for n=50, we get

> round(evalf(subs(n=50,H_n_asympt),20)); count(hier,size=50); evalf(""/");

The error is of about 1% for . A complete asymptotic expansion can be obtained by this method, by taking successive singular terms into account.

The number of classification stages

We examine the number of internal nodes in a classification. This corresponds to the number of classes actually created. The idea is to make use of "marks" in the form of Epsilon structures that have size 0 (and thus do not affect the combinatorial model).

> hier2:=[H,{H=Union(Z,Prod(class,Set(H,card>1))),class=Epsilon},labelled]:

Such marks do not affect the combinatorial model:

> seq(count(hier,size=j),j=0..11);

> seq(count(hier2,size=j),j=0..11);

(We change the formatting procedure to take Prod into account.)

> lreduce:=proc(e) eval(subs({Set=proc() {args} end, Sequence=proc() [args] end, Prod=``},e)) end:

Here is a random object with "class" marking classification nodes:

> lreduce(draw(hier2,size=20));

The system determined by equations over bivariate generating functions can be solved by Maple:

> gfeqns(op(2..3,hier2),z,[[u,class]]);

> H_zu:=solve(H=z+u*(exp(H)-1-H),H);

One gets averages by differentiation:

> H1_z:=subs(u=1,diff(H_zu,u));

Numerically, the mean number of nodes in a random classification tree of size , when divided by , is for ,

> Digits:=5: evalf(series(H1_z,z=0,22)): seq(coeff(",z,j)/count(hier,size=j)/j*j!,j=1..20);

This suggests that a random classification may have about classification stages.

We can in fact analyse this rigorously, using the asymptotic method already employed for counts.

> H1_s:=subs(z=rho*(1-Delta^2),H1_z):
H1_sing:=map(simplify,series(H1_s,Delta=0,5));
H1_n_asympt:=n!*asympt(coeff(H1_sing,Delta,-1)*rho^(-n)*subs({cos(Pi*n)=1,O=0},simplify(asympt(binomial(-1/2,n),n,2))),n);

> C_classif:=asympt(H1_n_asympt/H_n_asympt,n,1); evalf(",20);

Thus, we have obtained (easily!) a new Theorem . In a random classification tree, the number of classification stages (internal nodes) is asymptotic to

.

Degrees in random classification trees

The corresponding generating functions are now outside of the range of implicit functions that Maple knows about. Thus, a separate mathematical analysis is needed. However, an empirical analysis based on small sizes is already quite informative. The following code builds a specification where nodes of degree are marked. The principle is the obvious set-theoretic equation

.

The code uses combstruct[gfeqns] to generate the system of equations for each degree that is then expanded. In passing, it prints the corresponding generating function:

> deg_hier:=proc(k) local j,spec,n,dHH;
spec:=[H,{
H=Union(Z,Union(Set(H,card>k)),Prod(classif,Set(H,card=k)),seq(Set(H,card=j),j=2..k-1)),
classif=Epsilon},labelled];
dHH:=subs(u=1,diff(RootOf(subs({Z(z,u)=z,classif(z,u)=u,H(z,u)=H},
H(z,u)=subs(gfeqns(op(2..3,spec),z,[[u,classif]]),H(z,u))),H),u));
print(dHH);
seq(evalf(coeff(series(subs(u=1,dHH),z,27),z,n)/count(spec,size=n)*n!/n,5),n=1..25)
end:

> deg_hier(2);

> deg_hier(3);

> deg_hier(4);

> deg_hier(5);

Thus a random classification on elements seems to have on average about

about binary nodes;

about ternary nodes;

about quaternary nodes.

These results are consistent with the proved result that the total number of internal nodes is on average . The simple pattern revealed by this computation suggests a formal proof (by singularity analysis) that the distribution of degrees in fact obeys a modified Poisson law. The following theorem, first found while developing this worksheet, appears to be new:

Theorem . The probability that a random internal node in a random hierarchy of size has degree satisfies asymptotically a truncated Poisson law

> tau:=sqrt(2*log(2)-1);
S:=expand(sum(exp(-tau)*tau^(k-1)/(k-1)!,k=2..infinity));
Pr(deg=k)=normal(1/S*exp(-tau)*tau^(k-1)/(k-1)!);

Equivalently, the mean number of nodes of degree is asymptotic to

> C_classif/S*exp(-tau)*tau^(k-1)/(k-1)!;

Numerically, this evaluates to

> evalf([seq(",k=2..10)]);

These figures are consistent with what was found on sizes near 20. They show that nodes of degree 5 and higher have negligible chances of occurring.

Alternative models

Unlabelled hierarchies

A number of related models can be similarly analyzed. We examine here:

Unlabelled hierarchies: these represent the types of trees when one considers the elements to be classified as "indistinguishable". What we obtain is then reminiscent of chemical molecules (with an unrealistic element that would be capable of an arbitray valency).

Planar hierarchies, where one distinguishes the order between decsendents of classification node.

For unlabelled, hierarchies, we just need to change the qualifier of specifications to "unlabelled".

> hier4:=[H,{H=Union(Z,Set(H,card>1))},unlabelled]:

> ureduce:=proc(e) eval(subs({Set=proc() {[args]} end,Prod=proc() ``(args) end, Sequence=proc() [args] end},e)) end:

> ureduce(draw(hier4,size=20));

Notice that internally, the setting up of counting tables is more complex as it involves a fragment of Polya's theory. The counting results grow much more slowly, since we distinguish fewer configurations.

> seq(count(hier4,size=j),j=0..30);

> for j to 6 do j,map(ureduce,allstructs(hier4,size=j)) od;

Planar hierarchies

We only need to change Set into Sequence to get the right classification:

> hier5:=[H,{H=Union(Z,Sequence(H,card>1))},unlabelled]:

> ureduce:=proc(e) eval(subs({Set=proc() {[args]} end,Prod=proc() ``(args) end, Sequence=proc() [args] end},e)) end:

> ureduce(draw(hier5,size=50));

The counting sequence is

> seq(count(hier5,size=j),j=0..30);

This is found as Sequence M2898 in the Encyclopedia of Integer Sequences by Sloane and Plouffe and is known as Schroeder's second sequence.This sequence has a dignified history and Stanley noticed recently that the element already appears in Plutarch's [AD50- AD120 (!)] biographical notes on Hipparchus.

> gfsolve(op(2..3,hier5),z);

> H5_z:=subs(",H(z));

> series(H5_z,z=0,11);

Here is finally one quick way to obtain a simple recurrence for these numbers: first guess the recurrence, then check your guess. This, and many alternatives are encapsulated in the Gfun package.

> with(gfun):
listtorec([seq(count(hier5,size=j),j=0..30)],u(n));

> rectodiffeq(op(1,"),u(n),Y(z));

> dsolve(",Y(z));

Conclusion

Various models of random classification trees can be analysed both theoretically and empirically. Random generation is easy and the experiments lead to new conjectures (like the degree distribution) and even theorems (like the analysis of the number of classification stages). Returning to statistics, some properties of random trees appear to be present accross all models: for instance nodes of even moderately large degrees, , are highly infrequent, and branching is predominantly binary. General observations of this type may be used to help distinguish classification trees without informational content ("random" trees) from meaningful ones.