resummation.html

Borel Resummation of Divergent Series Using Gfun

Frédéric Chyzak, Marianne Durand, and Bruno Salvy

June, 2001

Abstract : We ex pand on ideas of Balser, Lutz, and Schäfke by showing how coefficients and integrals involved in calculations related to the analytic continuation of Borel transforms obey simple recurrences that lead to efficient numerical computations. This work is a follow-up to a talk by Donald Lutz at our Algorithms seminar, and summarized in [Durand].

1. Borel-Laplace resummation and Euler acc eleration

Starting with a linear differential equation with polynomial coefficients satisfied by a formal power series

it is possible to compute a differential equation satisfied by the Borel transform of . We assume that is Gevrey 1, which means that for some constants and , so that the Borel transform of defined by

is convergent on some neighbourhood of the origin. The Borel transform has an "inverse", the Laplace transform defined by

Provided this integral converges, the function it defines has for expansion as +. Then applying the change of variable to the integral computes the acceleration "a la Euler" [Lutz et al.]

We note

and ,

where is the functional inverse of the rational function . In terms of formal power series, the product equals the Taylor expansion of

where the integrals are independent of .

This process is illustrated in the present worksheet using a simple mapping function on the double confluent Heun equation. The Heun equation is the generic differential equation with four regular singular points located at 0, 1, c, and , see [DuLoRi92]. The double confluent Heun equation is obtained by letting the singularity located at c tend to the one located at , and the singularity located at 1 tend to 0. The equation obtained then has two irregular
singular points located at 0 and . The example we study is the double confluent Heun equation in the form

>

> readlib(gfun):

Since the point of interest is infinity and the gfun package works at the origin, we first change the variable (using gfun ):

> heunp:=gfun[algebraicsubs](heun_infp,z*f-1,f(z));

We concentrate on the following set of special values for the parameters:

>

Substitution of these parameters in the differential equation gives

> heun:=subs(paramform,heunp);

From this equation, we obtain a recurrence equation for the Taylor series coefficients

> recheunseries:=gfun[diffeqtorec](heun,f(z),u(n));

This recurrence yields an efficient procedure to evaluate the coeffici ents recursively:

> heundiv:=gfun[rectoproc](recheunseries union {u(1)=1/2},u(n),remember);

From this procedure, the divergence is clear from the growth of the first coefficients:

> seq(heundiv(i),i=1..15);

The generating function associated with the sequence is divergent. It is possible here to approach the corresponding function using summation to the least term. This method consists in summing the terms up to the smallest one. Under certain conditions that are fulfilled here, the total differs from the function by the value of this smallest term.

>

> plot('calculheundiv'(heundiv,z),z=0..0.3);

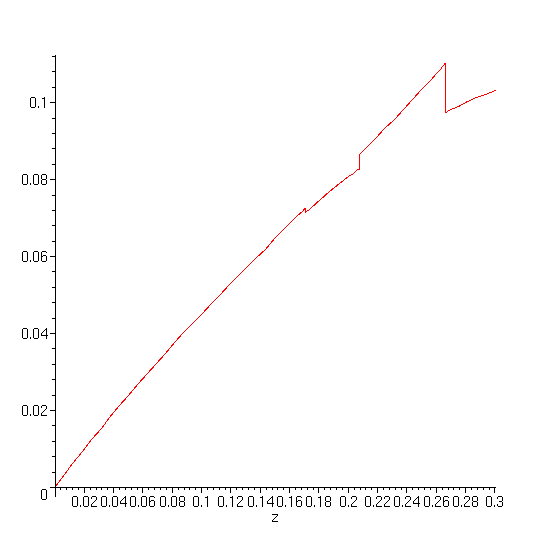
As tends to infinity, the imprecision of this summation grows quickly.

2. Differential equation satisfied by the Borel transform

The class of solutions of linear differential equations enjoys many closure properties which are implemented in the gfun package for the case of equations with polynomial coefficients. One of them is closure under Borel transform. Here is the differential equation satisfied by the Borel transform of the divergent solution of the Heun equation:

> bdeqp:=op(select(has,gfun[borel](heunp,f(z),'diffeq'),z));

and the equation specialized at the parameters

> bdeq:=subs(paramform,bdeqp):

From this follows the recurrence satisfied by the Taylor coefficients of the Borel transform:

> collect(gfun[diffeqtorec](bdeqp,f(z),a(n)),a,factor);

Check:

> l15:=gfun[rectoproc]({subs(paramform,%),a(0)=0,a(1)=1/2},a(n),list)(15);

This list corresponds to the list above, the th element being scaled by .

This differential equation and this recurrence can be used to compute (but not necessarily fast) the analytic continuation of the Borel transform.

3. The coefficients of the composition with an algebraic function satisfy a linear recurrence

This is another closure property of solutions of linear differential equation that we exploit here. The coefficients are defined by

where is a rational function and is defined by

On the example of the Heun equation, with we obtain

>

> dneqp:=gfun[algebraicsubs](bdeqp,eq,f(z));

and the equation when the parameters are specialized:

> dneq:=gfun[algebraicsubs](bdeq,eq,f(z));

The linear recurrence satisfied by the follows directly

> dnRec:=op(select(has,gfun[diffeqtorec](dneq,f(z),a(n)),n));

4. The integrals satisfy a linear recurrence

The property above does not depend on the specific divergent series that one is resumming. This allows one to precompute efficiently the integrals given the mapping function . Indeed the general theory of holonomic function has recently led to symbolic summation and integration algorithms that turn out to apply to the integral representation of . The goal of these algorithms is to derive (systems of) linear functional equations, differential or difference, satisfied by a sum or an integral. We now proceed to use a prototypical implementation of them in the package Mgfun to obtain a recurrence on the . Then, we prove a theorem that by-passes the general theory of holonomic functions, and recover the same recurrence in a more direct way.

(This section uses a version of Mgfun that is not distributed yet.)

> readlib(Mgfun):

>

> h[n](t):=%[1];

> H[n](t):=%%[2];

The meaning of the previous computation is that the differential equation

holds. This can be viewed as a differential-difference relation satisfied by the integrand . Now, integrating between and returns a non-homogeneous differential equation in the integral

namely

where the integral rewrites in terms of as

> Int(h[n](t),t=-1..1)=eval(subs(_f=unapply(q[n](z),n,t),ct[1]));

As to the non-homogeneous part , we readily evaluate it, verifying that it is 0 by chance.

> H[n](t):=factor(eval(subs(_f=unapply(F,n,t),H[n](t))));

> assume(z>0); assume(n,integer); factor(simplify(limit(op(2,%),t=1)-limit(op(2,%),t=-1))): non_hom:=subs([z='z',n='n'],%); z:='z': n:='n':

Consequently, we have obtained the following recurrence on the integrals .

> collect(eval(subs(_f=unapply(q[n](z),n,t),ct[1])),q,factor)=0;

> collect(subs(n=n-4,%),q,factor);

More generally, a differential equation with respect to , or even a system of mixed differential-difference equations could be obtained by the same algorithms.

The following result had not been noticed by Lutz et al., but might prove useful in numerical computations.

Theorem . With the above notations, let

be the linear recurrence satisfied by the Taylor coefficients at the origin of a power series solution of the first-order linear differential equation

Then the integrals satisfy the recurrence

Proof. The differential equation in the statement above is satisfied by the function

Since the integrals rewrite as

by integration by parts and differentiation under the integral sign, they satisfy the announced linear recurrence.

The following one-line procedure computes a recurrence on the integral

where is the functional inverse of a rational function . It takes as input where all the arguments except the first one are symbols that appear in the output linear recurrence relating the .

>

Example:

> qnRec:=recqnofz(1/(1-t)^2-1,t,q,n,z);

We have obtained the same recurrence as when using Mgfun .

> qnRec:=applyop(factor,[2,2],applyop(collect,[2,1],readlib(isolate)(subs(n=n+1,qnRec),q(n)),q,normal));

5. Numerical experiments

We know the recurrence followed by the , and we now have to compute initial conditions. By applying the change of variable , we obtain

which gives the following initial condition

> phi:=subs(z=u,solve(eq,f));

> assume(z>0):

> q0:=int(exp(-phi/z)*diff(phi,u),u =0..1);

> q0:=subs(z='z',q0); z:='z':

Note that this initial value is a posteriori obvious.

Thus we now have both recurrence and initial condition. The solution to the recurrence equation qnRec is a dominated solution, which means that any numerical error grows exponentially. To avoid this, we run the recurrence backwards from any non trivial initial conditions. The dominating solution disappears quickly, and we obtain the solution because when the recurrence is run backwards it becomes a dominating solution. We therefore add a parameter indicating from where we start running backwards.

> eval(collect(op(2,isolate(subs(n=n+3,qnRec),q(n))),q,normal),q=proc(n) q(n,z,NN) end);

>

Here is a procedure to compute numerically.

> `evalf/q/digits`:=0:

>

> dnproc:=gfun[rectoproc](dnRec,a(n),remember):

Here is a procedure to compute numerically.

> `evalf/d/digits`:=0:

>

Finally, the following procedure computes values of the double confluent Heun function as follows. First, an upper value of is selected and is used in the backward recurrence to compute the scaling to use for in view of the actual initial condition. Then the summation is performed up to the th term. If the relative error of the last term is larger than , then is doubled and the computation starts again. Note that option remember has been used in so as to avoid duplicating some of the work.

> time(evalf(q(0,10.2,3000),21));

> valheun:=subs(_q0=q0,proc(z)
local tot,i,N,NN,lambda,st,D;
N:=10;
st:=time();
do
N:=floor(2*N);
NN:=N+floor(sqrt(N))+10;
D:=Digits+3*ilog10(N) +floor(log(N));
lambda:=_q0/evalf(q(0,z,NN),D);

tot:=add(evalf(d(i),D)*evalf(q(i,z,NN),D),i=1..N)*lambda;
if abs(evalf(d(N),D)*evalf(q(N,z,NN),D)*lambda)<abs(tot)*10^(-Digits) then break fi;
od;
userinfo(1,valheun,"N=",N,"z=",1.0*z,"time:",time()-st,"digits:",D);
tot;
end):

We print information on the number of terms and time used for each point in a plot of the solution from 0 to 15:

>

> plot(valheun,0..50);

valheun:   "N="   80   "z="   1.089857709   "time:"   .141   "digits:"   17

valheun:   "N="   160   "z="   2.038137074   "time:"   .270   "digits:"   21

valheun:   "N="   320   "z="   3.104576397   "time:"   .579   "digits:"   21

valheun:   "N="   320   "z="   4.178084772   "time:"   .571   "digits:"   21

valheun:   "N="   320   "z="   5.246490950   "time:"   .599   "digits:"   21

valheun:   "N="   640   "z="   6.237040242   "time:"   1.221   "digits:"   22

valheun:   "N="   640   "z="   7.262696659   "time:"   1.080   "digits:"   22

valheun:   "N="   640   "z="   8.323431992   "time:"   1.129   "digits:"   22

valheun:   "N="   640   "z="   9.380765534   "time:"   1.240   "digits:"   22

valheun:   "N="   640   "z="   10.46836305   "time:"   1.201   "digits:"   22

valheun:   "N="   1280   "z="   11.42631952   "time:"   2.520   "digits:"   26

valheun:   "N="   1280   "z="   12.50475163   "time:"   2.369   "digits:"   26

valheun:   "N="   1280   "z="   13.58761188   "time:"   2.601   "digits:"   26

valheun:   "N="   1280   "z="   14.63114838   "time:"   2.750   "digits:"   26

valheun:   "N="   1280   "z="   15.57877949   "time:"   2.800   "digits:"   26

valheun:   "N="   1280   "z="   16.70560455   "time:"   3.110   "digits:"   26

valheun:   "N="   1280   "z="   17.66017317   "time:"   3.219   "digits:"   26

valheun:   "N="   1280   "z="   18.77056341   "time:"   3.340   "digits:"   26

valheun:   "N="   2560   "z="   19.75344692   "time:"   7.290   "digits:"   26

valheun:   "N="   2560   "z="   20.83182591   "time:"   8.091   "digits:"   26

valheun:   "N="   2560   "z="   21.85869773   "time:"   8.440   "digits:"   26

valheun:   "N="   2560   "z="   22.93013074   "time:"   9.180   "digits:"   26

valheun:   "N="   2560   "z="   23.91404071   "time:"   9.710   "digits:"   26

valheun:   "N="   2560   "z="   24.97532053   "time:"   10.209   "digits:"   26

valheun:   "N="   2560   "z="   26.07769200   "time:"   10.941   "digits:"   26

valheun:   "N="   2560   "z="   27.03730960   "time:"   11.229   "digits:"   26

valheun:   "N="   2560   "z="   28.07372290   "time:"   11.961   "digits:"   26

valheun:   "N="   2560   "z="   29.14443926   "time:"   12.589   "digits:"   26

valheun:   "N="   2560   "z="   30.19192632   "time:"   12.810   "digits:"   26

valheun:   "N="   2560   "z="   31.20542392   "time:"   13.741   "digits:"   26

valheun:   "N="   5120   "z="   32.33074020   "time:"   20.060   "digits:"   27

valheun:   "N="   5120   "z="   33.34188693   "time:"   12.880   "digits:"   27

valheun:   "N="   5120   "z="   34.42150189   "time:"   15.039   "digits:"   27

valheun:   "N="   5120   "z="   35.39979350   "time:"   17.241   "digits:"   27

valheun:   "N="   5120   "z="   36.46932464   "time:"   19.520   "digits:"   27

valheun:   "N="   5120   "z="   37.47567008   "time:"   21.760   "digits:"   27

valheun:   "N="   5120   "z="   38.52759104   "time:"   24.110   "digits:"   27

valheun:   "N="   5120   "z="   39.55603605   "time:"   26.450   "digits:"   27

valheun:   "N="   5120   "z="   40.63272267   "time:"   28.740   "digits:"   27

valheun:   "N="   5120   "z="   41.66969985   "time:"   31.479   "digits:"   27

valheun:   "N="   5120   "z="   42.73015878   "time:"   33.841   "digits:"   27

valheun:   "N="   5120   "z="   43.78183659   "time:"   36.099   "digits:"   27

valheun:   "N="   5120   "z="   44.74821926   "time:"   39.000   "digits:"   27

valheun:   "N="   5120   "z="   45.85580287   "time:"   40.981   "digits:"   27

valheun:   "N="   5120   "z="   46.84643885   "time:"   43.800   "digits:"   27

valheun:   "N="   5120   "z="   47.90266342   "time:"   45.850   "digits:"   27

valheun:   "N="   5120   "z="   48.91360511   "time:"   48.260   "digits:"   27

valheun:   "N="   5120   "z="   50.0   "time:"   50.699   "digits:"   27

valheun:   "N="   160   "z="   1.563997392   "time:"   1.450   "digits:"   21

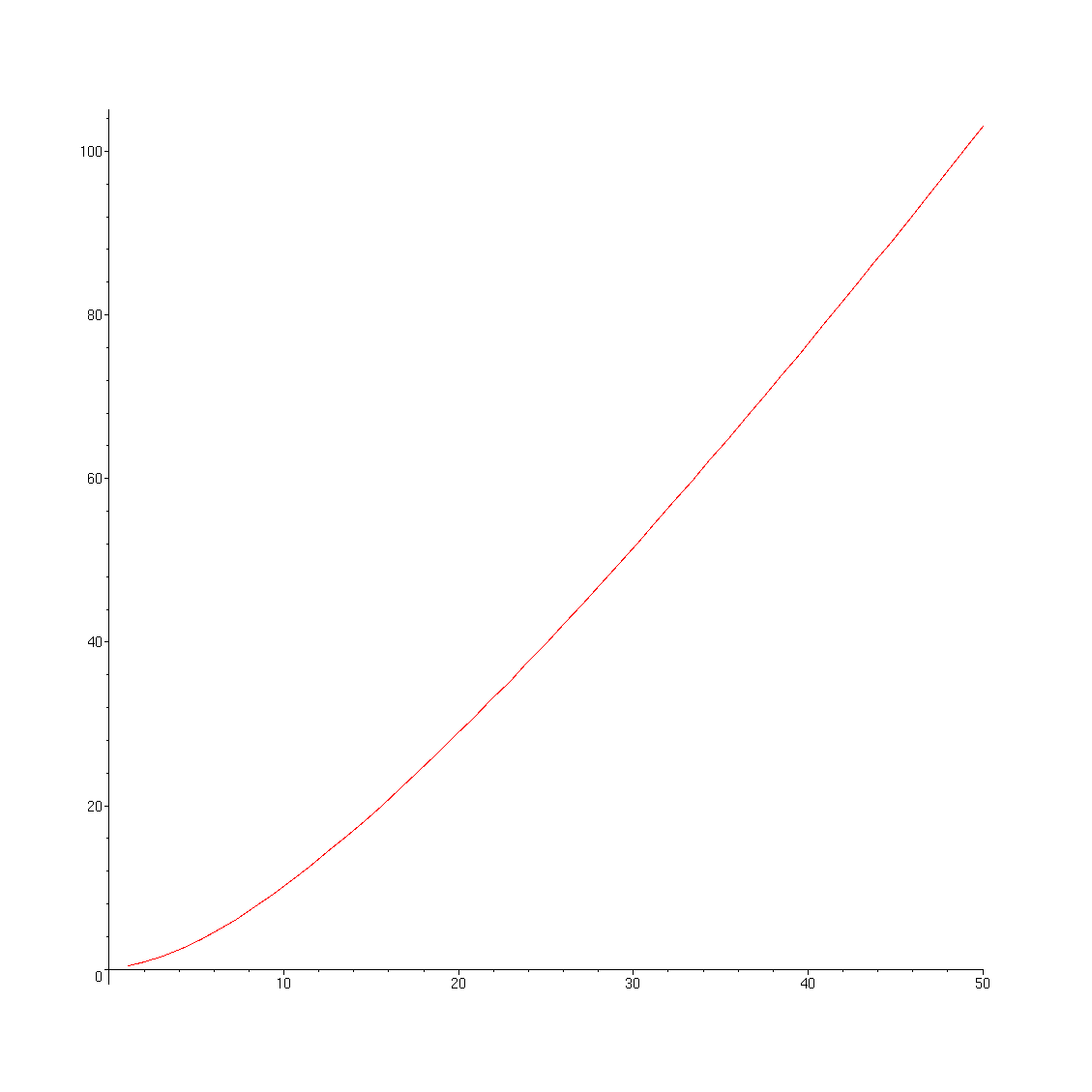
This curve is to be contrasted with the irregular plot we got from the same series using summation to the least term.

Sections 1 and 2 of this worksheet only depend on the Heun differential equation, and can easily be adapted to any linear differential equation. Sections 3 and 4 compute the recurrences satisfied by the coefficients and , which depend on the choice of the mapping function only for , and on the differential equation as well for . Section 5 details the numerical computations. It depends on and on the recurrences found in the previous sections. This worksheet can be adapted to another mapping function and to another linear differential equation.

References

[Lutz et al.] On the convergence of Borel approximants , by W. Balser, D. A. Lutz and R. Schäfke, (2000). Preprint.

[DuLoRi92] Kovacic's Algorithm and Its Application to Some Families of Special Functions , by Anne Duval and Michèle Loday-Richaud, Applicable Algebra in Engineering, Communication and Computing , (1992), vol. 3, p. 211-246.

[Durand] On the convergence of Borel approximants [summary of a talk by Donald Lutz] , by Marianne Durand, (2001). To appear in: Algorithms Seminar, 2000-2001 , INRIA Research Report.