ROBUSTNESS IN RANDOM INTERCONNECTIONS GRAPHS

Philippe Flajolet, January 11, 1998

(Based on joint work with Kostas Hatzis, Patras)

Random graphs are usually studied by the probabilistic method that is based on inequalities and on approximations of random variables. Many models that appear in this context can however be subjected to analytic methods. This worksheet explores one such situation using Combstruct , Gfun , and the Maple system. The objective is to characterise the interplay between three parameters of a random graph: its density (number of edges), its robustness to link failures, and its connectivity by short paths.

A triple , where is a graph, and are two designated nodes (the source and the target), is said to be -robust if and are connected by at least two edge-disjoint vertices of length exactly . This definition captures an intuitive notion of robustness to link failures, since and will remain connected by "short" paths even in the event of a link (i.e., edge) becoming unavailable in the interconnection graph represented by .

The random graph model is that of where the graph has vertices and each of the possible edges is independently taken with probability . Under this model, and because of the symmetry it implies with respect to the naming of nodes, it is strictly equivalent to examine robustness properties between a fixed source and destination or between a random pair of nodes . For definiteness, we adopt the latter formulation. A graph with very samll will not be robust, while a graph with close to 1 will have a high number of edge-disjoint paths of small length. The purpose is to evaluate the threshold value of from which -robustness becomes likely. In this worksheet, we focus on the problem of estimating the mean number of edge-disjoint pairs of length between a random source and a random target, and deduce the associated threshold.

The analysis proceeds in stages:

- Step 1 . Enumerate the number of pairs of paths of length connecting nodes and on a line, so that both paths use the same set of nodes .This is really a problem of counting so-called avoiding permutations defined as cyclic permutations with constraints on their so-called "succession gaps", i.e., the values of the differences between succesive values that are constrained not to belong to the set . This steps itself decomposes into:

S tep 1a . Enumerate so-called templates that are skelettons of permutations with a distinguished set of exceptions .

Step 1b . Transform the counting of templates into enumeration of permutations with a distinguished set of exceptions and conclude by means of the Principle of Inclusion-Exclusion , a classical combinatorial principle.

- Step 2 . Modify the model in order to allow for nodes taken from outside the segment . We then count avoiding paths that may borrow "outer nodes". This situation models the original random graph problem by allowing nodes taken from the whole pool of nodes that are available from the graph .

- Step 3 . Return to the original random graph problem and obtain the expected number of edge-disjoint pairs between a source and a destination in a random graph that obeys the model.

References .

[Comtet, 1974] : L. Comtet, Advanced Combinatorics , Reidel, 1974.

[EIS]: N. Sloane and S. Plouffe, The Encyclopedia of Integer Sequences , Academic Press, 1995.

This Maple worksheet is based on the current versions of the Maple packages combstruct and gfun (for version V.4) that can be found under http://www-rocq.inria.fr/algo/ .

> restart;

> with(combstruct);

> with(gfun);

1. Permutations with constrained succession gaps

The goal of this section is to enumerate permutations of that are cyclic, of the form , and with no succession gap in . We call such permutations avoiding permutations . In another language, what is the number of paths of length n-1 that join 1 to and have no edge in common with those of the line graph defined by the interval ?

There are no such paths for . Surprisingly enough, the first nontrivial configurations occur at (try it!), namely

{[1, 4, 2, 5, 3, 6], [1, 3, 5, 2, 4, 6]}

and for , one has

{[1, 3, 6, 4, 2, 5, 7], [1, 3, 5, 2, 6, 4, 7], [1, 4, 6, 2, 5, 3, 7], [1, 4, 2, 6, 3, 5, 7], [1, 5, 3, 6, 4, 2, 7],
[1, 5, 3, 6, 2, 4, 7], [1, 5, 2, 4, 6, 3, 7], [1, 4, 6, 3, 5, 2, 7], [1, 6, 3, 5, 2, 4, 7], [1, 6, 4, 2, 5, 3, 7]}
so that the numbers are . A brute force enumeration routine based on the predefined structures availaible under Combstruct is given below.

1.1. Templates

A template is a scheme that specifies which "bits and pieces" of the interval may be exceptions. We firtst need to enumerate templates.

In combstruct, we specify templates as decompositions of the interval into blocks that are either

-- isolated points ,

-- blocks of contiguous unit intervals (based at integer points) oriented left-to-right ,

-- blocks of contiguous unit intervals (based at integer points) oriented right-to-left .

A template must start with an or block and end similarly with an or block.

For instance, for , the template

will correspond to any cyclic permutation that has successions of values (in the cycle traversal)

1,2; 2,3; 5,6; 11,10; 10,9; 12,13

as distinguished exceptions to the basic constraint of avoiding permutations.

The combinatorial specification

First a preliminary specification. Let be a binary alphabet. The collection of strings beginning and ending with a letter is described by

> sp0:=S=Prod(Sequence(Prod(a,Sequence(b))),a);

(It suffices to decompose according to each occurrence of the letter .)

Now, the three types of blocks in a template are described by

> sp1:=Prod(begin_blockP,Z,end_blockP); sp2:=Prod(begin_blockLR,Z,Sequence(Prod(mu_length,Z),card>=1),end_blockLR);
sp3:=Prod(begin_blockRL,Sequence(Prod(mu_length,Z),card>=1),Z,end_blockRL);

Clearly, and are combinatorially isomorphic. For reasons related to application of the inclusion exclusion argument, we keep track of the size (number of nodes of the basic interval graph) as well as of the length of blocks and of their or character. Then, the grammar of templates is:

> Q:=subs([a=Union(sp1,sp2),b=sp3],sp0), begin_blockP=Epsilon, end_blockP=Epsilon, begin_blockLR=Epsilon, end_blockLR=Epsilon, begin_blockRL=Epsilon, end_blockRL=Epsilon, mu_length=Epsilon;

> temp15:=draw([S,{Q},unlabelled],size=15);

> decode:=proc(e) subs([Prod=proc() args end,Sequence=proc() args end,mu_length=NULL,Epsilon=NULL], e); ["] end;

> decode(temp15);

> seq(count([S,{Q},unlabelled],size=n),n=0..20);

Generating functions

A trivariate generating function immediately results from the specification. There, records size, records the total number of blocks (needed for subsequent permutation enumerations since blocks should be chained to each other), and records the total length of or blocks (the number of distiguished exceptions needed for inclusion exclusion).

> gfsolve({Q},unlabelled,z,[[u,begin_blockP,begin_blockLR,begin_blockRL],[v,mu_length]]);

> f_zuv:=subs(",S(z,u,v));

This GF can be checked by comparing its Taylor expansion and exhaustive listing, at least for small size values.

> map(expand,series(f_zuv,z));

The exhaustive listing is given by Combstruct[allstructs]

> map(decode,allstructs([S,{Q},unlabelled],size=3));

This corresponds to the correct listing

[[1],[2,3]]; [[1],[2],[3]]; [1,2,3]; [[1,2],3]

hence the monomial in the series expansion

1.2. Avoiding permutations

From templates to permutations

Let be the number of permutations of size with distinguished exceptions: is the number of permutations with distinguished special successions of the type or . Let be the number of permutations with no exception. Then, by inclusion exclusion, one has

.

(Roughly, one takes objects with at least 0 exception, subtract those with at least one exception, then add back those with at least two exceptions, etc.)

Let be the number of templates with a total of nodes, blocks, and a total length of the and blocks equal to . Then, by looking at all ways to connect the blocks, one has

, and , if ,

since any such connection is determined by an arbitrary permutation of the intermediate blocks.

The trivariate GF of the has been determined in the previous section. This shows a chain by which the are computable.

Observe that the extension of by linearity to an arbitrary series in is given by

.

That is to say, we just replace in expansions and apply the Euler integral

.

Thus, with = ,

the OGF satisfies

Generating functions

Start from the previously determined trivariate GF and apply the basic chain.

> f_zuv; map(expand,series(f_zuv,z));

For inclusion-exclusion, one must set :

> f_zu:=subs(v=-1,f_zuv);

Application of the -transformation (that count the number of ways to connect the blocks) requires the modified form

> k_zu:=normal(f_zu-(u-u^2)*subs(u=0,diff(f_zu,u)));

The OGF is here

> Q_z:=Int(k_zu*exp(-u)/u^2,u=0..infinity);

This solves the original counting problem numerically:

> Q_ser:=series(map(proc(e) int(e*exp(-u)/u^2,u=0..infinity) end,map(expand,convert(series(k_zu,z=0,15),polynom))),z,15);

Closed form . The quantity can be expressed in terms of the exponential integral:

> Q_z_closed:=eval(subs(Int=int,Q_z));

Since one deals with ordinary generating functions (OGF's), this is to be taken as a formal (asymptotic) series:

> map(normal,subs(z=1/y,Q_z_closed));map(simplify,asympt(",y,11));

.

The exponential integral ( ) involves the divergent series of factorials:

> Sum(n!*(-y)^(-n-1),n=0..infinity)=asympt(Ei(1,y)*exp(y),y,10);

The divergent series is also a hypergeometric series:

> series(hypergeom([1,1],[],z),z=0,9);

This gives rise to a general conversion procedure from Exponential integrals to hypergeometric forms:.

> convert_hypergeom:=proc(e) subs(Ei=proc(a,b) if a<>1 then ERROR(`unable to convert`) else exp(-b)/b*hypergeom([1,1],[],-1/b) fi end,e); simplify("); end;

Hence another closed form for the OGF of the

> Q_z_closed2:=convert_hypergeom(Q_z_closed);

Recurrences . Holonomic descriptions (by means of linear differential equations) can be obtained by Gfun[holexprtodiffeq] .

> Qz_ode0:=holexprtodiffeq(Q_z_closed2,Y(z));

> subs(Y(z)=Qz_ser,Qz_ode0):series(",z=0,11);

> Qz_ode:=subs(_C[0]=1,Qz_ode0);

The transformation to a linear recurrence is obtained by Gfun[diffeqtorec]

> Q_rec:=diffeqtorec({Qz_ode=0,Y(0)=0},Y(z),u(n));

This provides an algorithm that uses a linear number of arithmetic operations to determine the quantities .

> ha:=rectoproc(Q_rec,u(n),remember);

> ha(5);ha(50);ha(500);

Asymptotics.

An asymptotic pattern is easily inferred from numerical values..

> seq(ha(n)/(n-2)!*1.0,n=2..50);

> ha(500)/(498)!*1.0;

> exp(-2)=exp(-2.0);

And one can even guess the next term in an asymptotic expansion

> seq(n*(1-ha(n)/(n-2)!*exp(2.0)),n=6..50);

> nn:=500; ha(nn)/((nn-2)!*(1.0-2.0/nn)*exp(-2.0));

Thus, with reasonable certainty, we expect

.

The principle of a proof based on the generating function method is that

,

provided that the argument of the hypergeometric is a function that is analytic at the origin. Here, one has

> Q_z_closed2;

> -z*(z-1)/(1+z)=series(-z*(z-1)/(1+z),z=0,6);

so that the asymptotic proportion of legal permutations is provedly equal to :

> Qn_asy:=`Q `[n]/(n-2)!=exp(-2)*(1+O(1/n));

Results

We have thus obtained here a few original results regarding the enumeration of avoiding permutations.

Theorem 1 . The number of avoiding permutations has ordinary generating function:

> Q_z_closed=Q_z_closed2;

The coefficients satisfy the recurrence:

> Q_rec;

Accordingly, the ordinary generating function satisfies the corresponding linear ODE:

> map(factor,Qz_ode);

The coefficients satisfy the asymptotic estimate

> Qn_asy;

2. Paths with outer nodes

We now define avoiding paths . An avoiding path of size is a sequence of values from the set , where represents generically a node that does not belong to the interval , with the constraint that the initial value of the sequence is , the final value is , no successive value pairs can be of the type or , and no value from can occur more than once. Here are the sets of avoiding paths for sizes :

An avoiding path thus describes a path from to that is allowed to go through some "outer nodes". The goal is here to enumerate avoiding paths by size and by number of outer nodes conventionally represented by .

Let be the number of avoiding paths of size with outer nodes. Clearly, is the number of avoiding permutations. An extension of the earlier argument is thus needed.

2.1. Templates

One first needs templates on which an inclusion-exclusion argument is applied. The specifications are a simple modification of templates associated to avoiding permutations.

Let be a ternary alphabet. The collection of strings beginning with and and containing only one that occurs at the end is described by

> sp0:=S=Prod(Sequence(Prod(a,Sequence(b))),x);

(It suffices to decompose according to each occurrence of the letter .)

We first need so-called "outer points" that are taken from outer space.

> Outerpoints:=Sequence(Prod(Z,mu_outerpoint));

We also need "inner points".

> Innerpoints:=Sequence(Prod(Z,mu_innerpoint));

Size is defined as the cumulated number of points in the pair of paths that underlies an avoiding path in the sense above: it is thus equal to the length of the avoiding path plus the number of symbols corresponding to the outer nodes. We thus introduce a special notation for nodes of the integer line that are shared by the two paths:

> Z2:=Prod(Z,Z);

Now, the three types of blocks are described by

> sp1:=Prod(mu_block,Z2,Outerpoints,Innerpoints); sp2:=Prod(mu_block,Z2,Sequence(Prod(mu_length,Z2),card>=1),Outerpoints,Innerpoints);
sp3:=Prod(Sequence(Prod(mu_length,Z2),card>=1),Z2,Outerpoints,Innerpoints,mu_block);

(Clearly, and are combinatorially isomorphic.)

The blocks that can occur at the end are of type and can only be of type or but without outer points nor innerpoints.

> sp1x:=Prod(mu_block,Z2);

> sp2x:=Prod(mu_block,Z2,Sequence(Prod(mu_length,Z2),card>=1));

Then, the grammar is:

> Q:=subs([a=Union(sp1,sp2),b=sp3,x=Union(sp1x,sp2x)],sp0), mu_block=Epsilon, mu_length=Epsilon,mu_outerpoint=Epsilon,mu_innerpoint=Epsilon;

> draw([S,{Q},unlabelled],size=8);

> seq(count([S,{Q},unlabelled],size=n),n=0..20);

> for j from 0 to 6 do allstructs([S,{Q},unlabelled],size=j) od;

2.2. Generating functions

The trivariate generating function immediately results from the specification.

> gfsolve({Q},unlabelled,z,[[u,mu_block],[v,mu_length],[w1,mu_outerpoint],[w2,mu_innerpoint]]);

For inclusion-exclusion, one must set v=-1:

> f_zu:=factor(subs(v=-1,subs(",S(z,u,v,w1,w2))));

Application of the -transformation (that counts the number of ways to connect the blocks) requires the modified form

> h_zu:=factor(normal(f_zu-(u-u^2)*subs(u=0,diff(f_zu,u))));

This solves the original counting problem:

> Q_ser:=series(map(proc(e) int(e*exp(-u)/u^2,u=0..infinity) end,map(expand,convert(series(h_zu,z=0,12),polynom))),z,15);

There, the coefficient of counts the number of avoiding paths with size and with outer nodes.

Closed form and recurrences . The OGF is here

> Q_z:=Int(h_zu*exp(-u)/u^2,u=0..infinity);

And this can be expressed in terms of the exponential integral:

> Q_z_closed:=eval(subs(Int=int,Q_z));

Again, there is an "explicit form" of the OGF the problem

> Qz_closed2:=map(factor,convert_hypergeom(Q_z_closed));

> Qz_closed3:=factor(Qz_closed2-subs(hypergeom=0,Qz_closed2))+factor(subs(hypergeom=0,Qz_closed2));

The diagonal, where and appear with equal exponents, is then easily extracted.

> Q_order:=20: Qz_ser:=map(normal,series(Qz_closed3,z=0,Q_order+2)):subs([w1=w,w2=t/w],Qz_ser): subs([w1=w,w2=t/w],Qz_ser): map(series,",w=0,2*Q_order+5):Qzt_ser:=map(coeff,",w,0);

We thus get results that generalize the counting of avoiding permutations.

> subs(t=0,Qzt_ser);subs(t=1,Qzt_ser);

2.3. Exhaustive listings

Here's a procedure that lists balanced avoiding pairs exhaustively (by generating all permutations and filtering the relevant ones) and derives the counting polynomials. This fully confirms the GF computations done previously.

> test:=proc()
local i, perms, dontcares, poly, count1, p, p1, j, x, s, n, listing; n:=args[1];
perms:=combstruct[allstructs](Permutation([seq(i,i=2..n-1)]),size=n-2); dontcares := combstruct[allstructs](Subset({seq(i,i=2..n-1)}));
listing:={};
poly:=0;
for s in dontcares do
count1:=0;
for p in perms do p1:=[1,op(p),n];
for x in s do p1[x]:=-1; od;
for j from 1 to n-1 while abs(p1[j+1]-p1[j])<>1 do
od;
if j=n then count1:=count1+1; listing:=listing union {p1} fi;
od;
poly:=poly+count1*t^nops(s)/nops(s)!;
od;
if nargs>1 then RETURN(sort(listing)) fi;
RETURN(poly);
end;

> for j from 2 to 6 do j,test(j) od;

> for j from 2 to 6 do j,test(j,LIST_THEM_ALL) od;

> remove(has,test(6,LIST_THEM_ALL),-1);

> remove(has,test(7,LIST_THEM_ALL),-1);

These results confirm the GF computation of the previous subsection.

2.4. Explicit binomial formulae

We can now return to the GF of avoiding paths enumerated by size and number of outer nodes.

> Qz_closed3;

The coefficient of is obtained by straight expansion and avoiding paths are then enumerated by . The corresponding formulae are obtained directly by symbolic expansions (performed manually, though!)

> j:='j': C_formula:=C(n+2,j)=Sum(Sum( (-1)^(k1+k2)*(n-j-k1-k2)!*'B'(n-j-k1-k2,k1)* 'B'(n-j-k1+1,k2)*'B'(n-k1-k2,j)^2, k1=0..n-j-k2), k2=0..n-j);

where is the binomial, coefficient .

> Bin:=proc(n,k) if n<0 or k<0 then 0 else binomial(n,k) fi; end;

> coef:=proc(n,j) option remember; local k1,k2;
add( add( (-1)^(k1+k2)*(n-j-k1-k2)!*Bin(n-j-k1-k2,k1)* Bin(n-j-k1+1,k2)*Bin(n-k1-k2,j)^2, k1=0..n-j-k2), k2=0..n-j); end;

> Coef:=proc(n,j) local r; option remember; r:=coef(n-2,j);
if j=0 then r:=r-(-1)^n fi; r; end;

This gives the generating polynomials .

> co:=proc(n,t) local j; option remember; add(Coef(n,j)*t^j,j=0..n) end;

Here is a short table, again consistent with values obtained by exhaustive listing of small cases.

> for nn from 2 to 8 do 'co'(nn,t)=co(nn,t) od;

Results

Theorem 2 . The number of avoiding paths counted by size and by number of outer nodes satisfies for

> C_formula;

For , the formula simplifies and provides the number of avoiding permutations

> 'Q[n+2]'=subs(j=0,B(n-k1-k2,0)=1,op(2,"))-(-1)^n;

( denotes a binomial coefficient.)

3. The random graph problem

We conclude this section by showing how to estimate the robustness of connections to link failures between a source and a target in a random graph that obeys the model, where edges between nodes are chosen independently with probability .

An avoiding pair of length in a graph is an unordered pair of paths, each of length that may share some nodes but are edge disjoint.The mean number of (unordered) avoiding pairs in a random graph obeying the model between an arbitrary source and an arbitary destination is an indicator of the robustness of the graph to a single link failure. This mean value is:

> l:='l': Numpath_formula:=1/2*1/(n*(n-1))*Sum(C(l+1,j)*B(n,l+1+j)*(l+1+j)!,j=0..l)*p^(2*l);

The argument is as follows. The coefficient corresponds to the fact that one takes unordered pairs of paths, the coefficient averages over all sources and destinations, and the arrangement numbers account for the number of ways to embed an avoiding path into a graph by choosing certain nodes and assigning them in some order to an avoiding path.

The -coefficients are as provided by Theorem 2 and still means binomial coefficient.

The procedure that implements the formula for the mean number of paths is then

> means:=proc(n,p,l) local j; option remember; 1/2*1/(n*(n-1))*add(Coef(l+1,j)*binomial(n,l+1+j)*(l+1+j)!,j=0..l+1)*p^(2*l); expand("); if l<=12 then factor(") else " fi end;

> for ll from 1 to 10 do means(n,p,ll) od;

Here is an instance for a graph of nodes, a probability of , so that the mean node degree is about :

> seq(subs(n=10^5,p=5.0*10^(-5),[ll,means(n,p,ll)]),ll=2..16);

It appears that there is a sharp threshold between and . This is to be compared with the number of nodes reachable from the root of a tree with node degree in steps: is just below while exceeds

The probability threshold after which the mean number of unordered pairs exceeds 1 is given by

> p0:=proc(nn,l) local p; fsolve(subs(n=nn,means(n,p,l))=1,p,0..1) end;

And this quantity is best visualised in terms of the mean node degree:

> delta:=proc(n,p) (n-1)*p; end;

For a graph of size , we have

> seq([ll,delta(10^5,p0(10^5,ll))],ll=2..10);

The thresholds are fairly sharp as attested by plots of the mean values of the number of (unordered) avoiding pairs when the probability increases (the horizontal axis gives the mean degree ).

> nn:=10^5: plot([seq(means(nn,delta/(nn-1),ll),ll=3..8)],delta=0..20,mu=0..1,thickness=3);

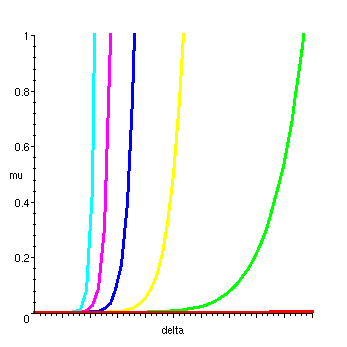
(The curves from left to right correspond to path length = 8, 7, 6, 5, 4, 3.)

Asymptotics . For dense graphs and large size, a numerical pattern clearly emerges. Here is what happens for mean degree and size :

> seq(subs(n=10^5,p=1.0*10^(-4),[ll,means(n,p,ll)]),ll=2..20);

The mantissas all start with 0.49. This corresponds to a regime where the distance is small so that only dominant terms in the mean value polynomial intervene. The mean number of avoiding pairs is then approximately

> mu=1/2*n^(2*l)*p^(2*l+2)*(1+o(1));

or, in terms of the mean degree parameter :

> mu=1/2*delta^(2*l)*p^2;

This simplified formula explains the numerical regularities seen above, where the mean number increases by a factor of about when increases by 1.

Conversely, a clear example of nonasymptotic regime is provided by and , that is .

> nn:=10^3; dd:=10.0^(1/8); pp:=dd/(nn-1);for ll from 10 to 28 by 2 do l=ll,ExactMean=evalf(subs(n=nn,p=pp,means(n,p,ll)),5),ApproxMean=evalf(1/2*nn^(2*ll)*pp^(2*ll+2),5) od;

The ratio between the exact formula and the simplified approximation is typically of about 1 to 2 or 1 to 4, with the approximation being systematically optimistic. An explanation is that, apart from asymptotic approximations in , the simplified formula precisely neglects the exclusion effect on edges and this is permissible only in dense large graphs having high connectivity.

Conclusion

Permutations with constrained succession gaps are accessible to combstruct and gfun . This is achieved via the notion of templates that are nicely decomposable in conjunction with the inclusion-exclusion principle that is expressed by a simple integral transformation. Generating functions and recurrences result automatically and this leads to explicit binomial formulae. An application to robustness in a random interconnection graph derives from this approach and we have shown how to determine the mean number of edge-disjoint pairs between a source and a target in such a random graph.