A SEATING ARRANGEMENT PROBLEM

Philippe Flajolet

(Version of January 15, 1997)

There are seats in a row at a luncheonette, and people sit down one at a time at random. They are unfriendly and so never sit next to one another. What is the expected number of persons to sit down?

The original problem is due to Freedmann and Shepp, and it appeared as Problem 62-3 in the 1962 volume of SIAM Review . There are various alternative formulations. One of them involves fatmen that need more than one stool to sit on. Another one is a simplified description of channel occupation for mobile telephones due to the Math. Center at Bell Labs: there are consecutive radio channels and stations arrive at random and try to grab a free channel; because of possible interferences, no station occupies a channel next to an already occupied one. What is the expected proportion of occupied channels?
Clearly, the number of occupied seats/channels lie somewhere between and . This worksheet explores the way the solution to this and similar problems may be found using the Gfun package. The common schema explored here is: (1) write down an immediate specification of the problem; (2) use the gfun[listtorec] procedure to guess the right differential equation; (3) exploit the results using Maple capabilities for integration and asymptotic expansion.

Basic equations

Let be the probability generating function (PGF) of the number of occupied seats when they are seats. In the Maple code below, we take implicitly as the generating variable. If the first individual to arrive occupies seat , then the number of occupied seats is 1 plus the number of occupied seats in plus the number of occupied seats in , as seats and have become unavailable. The subproblems of sizes and are of a similar nature. By the randomness assumption, takes each value in with equal probability, namely . This gives rise to a recurrence on random variables (the number of occupied seats) and on generating functions

> L[n]=1+L[K-2]+L[n-K-1], Pr(K=k)=1/n;g(n)=u/n*Sum(g(k-2)*g(n-k-1),k=1..n),g(-1)=1,g(0)=1,g(1)=u;

This recurrence determines the explicitly and is implemented by the following Maple code:

> g:=proc(n) local k; option remember;
if n<=0 then 1 elif n=1 then u else
expand(u/n*convert([seq(g(k-2)*g(n-k-1),k=1..n)],`+`));
fi
end:

> seq([j,g(j)],j=0..5);

For instance, when , there is probability that just one seat is occupied: this occurs only if the first person that arrives chooses the middle seat.

We then get the moments by successive differentiation.

> subs(u=1,diff([seq(g(j),j=0..20)],u));

> evalf(subs(u=1,diff([seq(g(j)/j,j=1..40)],u)),5);

This suggests that the mean occupation ration could be, for large, asymptotic to a constant with approximate value 44%.

The mean occupancy ratio

The easiest is to try a heuristic approach. As the recurrences for moments are linear, it is reasonable to expect them to be of the holonomic type. We thus compute a few dozen initial values and try to guess a recurrence with gfun[listtorec] .

> with(gfun);

> rec:=listtorec(subs(u=1,diff([seq(g(j),j=0..25)],u)),u(n));

The recurrence transforms into a differential equation by means of gfun[rectodiffeq]

> ode:=rectodiffeq(op(1,rec),u(n),Y(z));

Now, we are sure of the existence of a closed form for the generating function of averages, since any ODE of order 1 is solvable by quadratures. The dsolve command of Maple does the job:

> M1_z:=factor(op(2,dsolve(ode,Y(z))));

We can check consistency with known values

> series(M1_z,z=0,30);

We can be also quite sure that the process makes sense if we compare as well with values that haven't been used at all in the "guessing" phase:

> subs(u=1,diff([seq(g(j),j=26..29)],u));

The generating function of expectations is meromorphic with only a pole at . In order to analyse the coefficients of the explicit solution found, we examine the singular expansion at the double pole :

> map(normal,series(M1_z,z=1,4));

By the principles of singularity analysis, it is enough to expand the singular part. This shows that the mean number of occupied seats satisfies the approximate formula

> m1:=1/2*(1-exp(-2))*(n+1)-exp(-2); evalf(m1,20); C1:=evalf(coeff(m1,n,1)):

The asymptotic approximation is in fact extremely good and is about for

> for j from 0 to 30 by 5 do j,evalf(subs(u=1,diff(g(j),u))-subs(n=j,m1),30) od;

In particular the constant found empirically to be close to 0.44 is precisely

> 1/2*(1-exp(-2))=evalf(1/2*(1-exp(-2)),30);

Distributional analysis

Whenever possible in analysis of algorithms, one should try to determine how characteristic the average case is. We show now that the standard deviation of the distribution of the number of occupied seats/channels is . By the Markov-Chebyshev inequalities, this means that, for large , almost all configurations must be close to the average predicted value.

First, we have access to the second (factorial) moments by a double differentiation.

> l2:=subs(u=1,diff([seq(g(j),j=0..25)],u,u));

The function gfun[listtorec] aims at detecting ("guessing") plausible linear recurrences with polynomial coefficients. It uses two parameters gfun[maxordereqn] , gfun[maxdegcoeff] , with default values 3 and 4 respectively, so that it is tuned for quick discovery of simple recurrences.

> gfun['maxordereqn'],gfun['maxdegcoeff'];
rec:=listtorec(l2,u(n));

The control parameters can be set to higher values.

> gfun['maxordereqn']:=8; gfun['maxdegcoeff']:=6;

We can now determine the right recurrence (we need more values):

> l2:=subs(u=1,diff([seq(g(j),j=0..55)],u,u)):

> rec2:=listtorec(l2,u(n));

The recurrence is of order 7. The generating function satisfies a differential equation of order 3 with coefficients of degree 7 (!!). It is rather remarkable that the dsolve command of Maple can solve this explicitly.

> ode2:=rectodiffeq(op(1,rec2),u(n),Y(z));

Note that a simple rational solution is detected by dsolve. This entails a reduction of order,

and a complete algorithm exists for order 2 (in fact that Maple succeeds in bypassing here).

> infolevel[dsolve]:=5: M2_z:=factor(op(2,dsolve(ode2,Y(z))));

dsolve/diffeq/polylinearODE: checking Euler equation
dsolve/diffeq/expsols: trying exponential solutions
dsolve/diffeq/expsols: rational solutions partially successful. Result(s)= (1-3*z)/(-1+z)^3
dsolve/diffeq/expsols_solvericcati: all solutions by polynomial part
dsolve/diffeq/expsols: expon. solutions partially successful. Result(s) = exp(Int((-2*z^2+z-2)/(z^2-z),z)), exp(Int((-4*z^2-2*z)/(-1+z^2),z))

The singular part at is analysed. For the variance this leads to approximate formulae.

> Moment2_sing:=map(simplify,series(M2_z+M1_z,z=1,3));

> var_n_asympt:=factor(collect(expand(convert([seq((-1)^j*coeff(Moment2_sing,z-1,j)*binomial(n-j-1,-j-1),j=-3..-1)],`+`)-m1^2),n,simplify));

Again, the approximations are extremely good:

> evalf(var_n_asympt,30);

> evalf(subs(n=50,var_n_asympt),30); evalf(subs(u=1,(diff(g(50),u,u)+diff(g(50),u)-diff(g(50),u)^2)),30);

We have in passing obtained a Theorem . In the random seating problem, the variance of the number of occupied seats when there are seats is asymptotic to

.

This result seems to be new (!). Convergence is extremely fast so that this formula is highly accurate. The standard deviation is found to be only about .

Distribution . A mean that is and a standard deviation that is entail that the distribution is concentrated around its mean with high probability. This also suggests that the distributions of the number of occupied seats could be asymptotically Gaussian.

> distr:=sort(map(proc(e) [op([2,2],e),op(1,e)] end,[op(evalf(g(60),4))]),proc(x,y) evalb(op(1,x)<op(1,y)) end):

> linalg[transpose](matrix(distr));

> plot(distr,style=POINT);

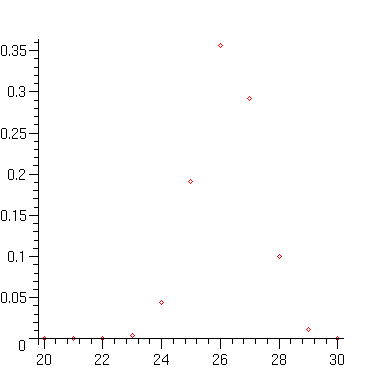
In 65% of the cases, the occupation is either 26 or 27; the probability of an extremely bad assignment (20 seats out of 60) is only about . In fact, a Gaussian law can be proved by adapting the bivariate analysis of patterns in binary search trees by Flajolet, Martinez, and Gourdon (1996).

Fatter men

The approach extends to the case where fatmen need seats on each side. The earlier case was . We consider here . This time, the number of occupied seats lies somewhere between and . Now, we let be the probability generating function (PGF) with the generating variable. The following procedure computes for a given size and the parameter .

> gb:=proc(n,b) local k; option remember;
if n<=0 then 1 elif n<=b then u else expand(u/n*convert([seq(gb(k-b-1,b)*gb(n-k-b,b),k=1..n)],`+`))
fi
end:

The probability generating functions are now:

> seq([j,gb(j,2)],j=0..6);

For instance, for , we have 2 occupied seats if the first arrival is on a side (this has probability ), which leaves the opposite seat available, and 1 occupied seat otherwise.

The moments are obtained by differentiation of the PGF:

> subs(u=1,diff([seq(gb(j,2),j=0..25)],u));

> evalf(subs(u=1,diff([seq(gb(j,2)/j,j=1..35)],u)),5);

This suggests an occupation ratio of about 28%, now.

Like before, we can guess a differential equation and attempt to solve it.

> lb1:=subs(u=1,diff([seq(gb(j,2),j=0..35)],u)): gfun['maxordereqn']:=5; gfun['maxdegcoeff']:=5; recb:=listtorec(lb1,u(n));

> rectodiffeq(op(1,recb),u(n),Y(z));

The differential equation is of first order, hence again solvable by quadratures

> solb:=dsolve(",Y(z));

dsolve/diffeq/dsol1: -> first order, first degree methods :
dsolve/diffeq/dsol1: trying linear bernoulli
dsolve/diffeq/linearsol: solving 1st order linear d.e.
dsolve/diffeq/dsol1: linear bernoulli successful

This time the solution involves the Gaussian error function ( erf ). The solution is singular at , with an apparent double pole.

> singb:=series(op(2,solb),z=1,3);

> c2:=factor(simplify(coeff(singb,z-1,-2))); c1:=factor(simplify(coeff(singb,z-1,-1))); C2:=evalf(c2):

This corresponds to an asymptotic form for the first moment

> mb1:=c2*(n+1)-c1; evalf(mb1,30);

Once more, the asymptotic approximation is extremely good, even for relatively small values of n.

> for j from 0 to 30 by 5 do j,evalf(subs(u=1,diff(gb(j,2),u))-subs(n=j,mb1),30) od;

This last example demonstrates the interest of preserving initial conditions whenever possible. The way Gfun and Maple manage them consistently is especially useful here.

Fatter men, even!

We follow the same schema and consider finally the situation where 3 seats/channels are unavailable next to an occupied seat. The number of occupied seats must now lie between n/4 and n/5.

> evalf(subs(u=1,diff([seq(gb(j,3)/j,j=1..35)],u)),5);

This suggests an occupation ratio of about 21%.

> lb1:=subs(u=1,diff([seq(gb(j,3),j=0..35)],u)): gfun['maxordereqn']:=6; gfun['maxdegcoeff']:=3; recb:=listtorec(lb1,u(n));

> gfun['maxdegcoeff']:=1; rectodiffeq(op(1,recb),u(n),Y(z));

The solution now involves integrals of cubic polynomials.

> solb:=dsolve(",Y(z)); singb:=series(op(2,solb),z=1,3);

dsolve/diffeq/dsol1: -> first order, first degree methods :
dsolve/diffeq/dsol1: trying linear bernoulli
dsolve/diffeq/linearsol: solving 1st order linear d.e.
dsolve/diffeq/dsol1: linear bernoulli successful

> c2:=factor(simplify(coeff(singb,z-1,-2))); c1:=factor(simplify(coeff(singb,z-1,-1))); C3:=evalf(c2):

> mb1:=c2*(n+1)-c1; evalf(mb1,30);

In particular, the mean occupatio ratio is an interesting integral that evaluates to .200973369978844243166574354875...

And finally, the approximation is still very good, being within 1% already for , although the asymptotic regime takes a little longer to establish

> for j from 0 to 30 by 5 do j,evalf(subs(u=1,diff(gb(j,3),u))-subs(n=j,mb1),30) od;

Conclusions

Our purpose here has been to demonstrate how one naturally arrives at the solution of a probabilistic problem using tools like Gfun. Once the solutions have been "guessed", it is possible to come back, think, and prove solutions. For instance, the problem of the mean leads to recurrences that involve history (summation) and a factor of ; thus, it is reasonable to expect to be within reach of the theory of holonomic functions on which Gfun is based, and rough bounds on the order of recurrences or differential equatiosn suffice to validate the "guesses". In this way, we have "naturally" rediscovered a solution of the generalized problem due to David Rothman (fatter men) and obtained a variance analysis for the basic problem that appears to be new. The whole session (including the variance computations) takes about 60 seconds of CPU time on a DEC-3000 station.

About the original problem, we may compare the mean seat occuptation to the best possible seating arrangement:

> for i from 1 to 3 do `C`.i/(1/(i+1)) od;

Thus, we have determined the price to be paid for random access: it is about 15% to 20%. As we saw repeatedly, the asymptotic approximations obtained are extremely good, already for . Also the distributional analysis, where a small variance is obtained, shows that the average-case is highly representative of what will be observed in practice.