PATTERNS IN WORDS

Bruno Salvy

(Version of February 7, 1997)

This worksheet applies combstruct and gfun to a simple combinatorial model of a problem from computational biology and the study of DNA sequences. The DNA can be viewed as a long text on an alphabet of four letters (A,C,G,T). Large fragments of this text are tabulated. In particular, there are huge bases of genes, a gene being a few thousand letters long. Given a short word, it is interesting to determine whether its number of occurrences in a gene (or a virus) is far away from the most probable number of occurrences. If this number of occurrences is very improbable, then this particular word may have a biological function.

The combinatorial model is rational. The text is a word on the alphabet (a,b,c,d) where all words of the same length are equiprobable. The probability that a pattern occurs times in the text depends on the way the pattern overlaps with itself.

> libname:=`/export/maplelib/5.4`,libname:

> with(combstruct): with(gfun):

Specification and univariate generating functions for the pattern abab

Working over the alphabet (a,b,c,d), we first concentrate on a specific pattern (abab). To attack problems related to occurrences of this pattern in words using combstruct, we first write a grammar which describes a corresponding automaton.This grammar recognizes all the words on (a,b,c,d). It is written in such a way that a mark (named Mark) is present in a word everytime the pattern abab occurs. Then counting the number of marks in a word gives the number of occurences of abab in it.

> G:={w=Union(Epsilon,Prod(a,wa),Prod(b,w),
Prod(c,w),Prod(d,w)),
wa=Union(Epsilon,Prod(a,wa),Prod(b,wab),
Prod(c,w),Prod(d,w)),
wab=Union(Epsilon,Prod(a,waba),Prod(b,w),
Prod(c,w),Prod(d,w)),
waba=Union(Epsilon,Prod(a,wa),Prod(b,Prod(Mark,w)),
Prod(c,w),Prod(d,w)),
Mark=Epsilon,a=Atom,b=Atom,c=Atom,d=Atom}:

We use the function combstruct[count] to check that the number of words of length is :

> count([w,G,unlabelled],size=10),4^10;

> count([w,G,unlabelled],size=20),4^20;

It is also possible to prove this by computing the generating function of the language with combstruct[gfsolve] :

> gfsolve(G,unlabelled,z);

> subs(",w(z));

The coefficient of in the Taylor expansion of this generating function is the number of words of length in the language, which confirms the correctness of our grammar.

Here are a few typical words of the language obtained by the uniform random generator provided by combstruct[draw] :

> to 20 do eval(subs(Prod=proc() args end,draw([w,G,unlabelled],size=30))) od;

Some of these words countain the pattern abab, as indicated by the letter `Mark' right after its occurrence.

Bivariate generating functions

From the grammar specification above, the command combstruct[gfsolve] can also be used to derive multivariate generating functions. From this, it is easy to compute the probability that the pattern occurs times in a random word of length , the expectation of the number of occurrences of the pattern in such a word, and the corresponding variance.

> gfsolve(G,unlabelled,z,[[u,Mark]]);

> sol:=subs(",w(z,u));

Fixed number of occurrences

We now consider the probabilities that abab occurs times, for . Using gfun , we can compute these probabilities for random words of length , with up to a few thousands.

> maxnb:=5:

> for i from 0 to maxnb do proba[i]:=coeff(S,u,i) od;

Since we want to investigate these probabilities for texts of large size (a typical gene is a few thousand letters long), we need the Taylor expansions of these rational functions for very large orders. These can be computed using gfun , which will first compute the linear recurrence satisfied by these Taylor coefficients ( gfun[diffeqtorec] ), and then exploit these recurrences to compute the series efficiently ( gfun[rectoproc] ):

> for i from 0 to maxnb do
rec:=diffeqtorec(y(z)-proba[i],y(z),u(n));
print(i,rec);
rec:=select(has,rec,n) union {seq(op(1,i)=evalf(op(2,i)),i=remove(has,rec,n))};
P[i]:=rectoproc(rec,u(n),remember)
od:

We now compute the probability that the pattern abab occurs 0,1,...,5 times in a word of length 1000:

> Digits:=30:for i from 0 to maxnb do i,P[i](1000) od;

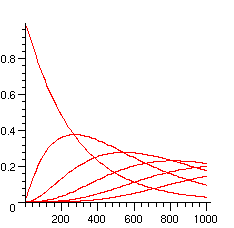
The following picture then shows how these probabilities evolve with the length of the word:

> plots[display]({seq(plot([seq([10*i,P[j](10*i)],i=1..100)]),j=0..maxnb)});

Similarly, the following picture indicates the probabilities that the pattern abab occurs at most times instead of exactly times

> plots[display]({seq(plot([seq([10*i,add(P[k](10*i),k=0..j)],i=1..100)]),j=0..maxnb)});

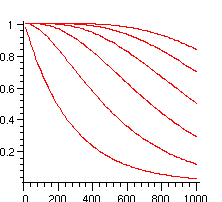
The complexity of these computations grows only linearly with the number of occurrences under study. Other kinds of constraints like number of occurrences larger than for fixed or between and also give rise to rational generating functions that can be extracted from the generating function GF and thus can be treated the same way.

Other patterns

All the above computation was derived from the grammar describing the language, a mark being appended to every occurrence of the pattern. It is actually easy to write a Maple procedure taking as input a word, and producing the corresponding combstruct grammar . Then the whole computation above can be reproduced for any pattern completely automatically.

> gengram:=proc(pattern::list({identical(a),identical(b),identical(c),identical(d)}))local i, eq, letter, state, j;
for i to nops(pattern) do for letter in [a,b,c,d] do for j from 0 to i-1 do if [op(1..i-j,pattern)]=[op(j+1..i-1,pattern),letter] then state[letter]:=cat(w,op(1..i-j,pattern)); break fi od; if j=i then state[letter]:=w fi od;eq[i]:=cat(w,op(1..i-1,pattern))=Union(Epsilon,seq(Prod(letter,state[letter]),letter=[a,b,c,d])) od; subs(cat(w,op(pattern))=Prod(Mark,w),{seq(eq[i],i=1..nops(pattern)),seq(letter=Atom,letter=[a,b,c,d]),Mark=Epsilon}) end;

Given a pattern, this procedure outputs the corresponding combstruct grammar. Thus for instance, using the pattern abab,

> gengram([a,b,a,b]);

we obtain the grammar we started with. It is now possible to study longer patterns easily. Here are the different states leading to the probability that the pattern abacab occurs twice in a word of length 5000:

First the grammar is generated

> G:=gengram([a,b,a,c,a,b]);

then the bivariate generating functions are derived

> gfsolve(G,unlabelled,z,[[u,Mark]]);

the generating function is then converted into a probability generating function by a simple substitution

> normal(subs(",z=z/4,w(z,u)));

extracting a coefficient we get the probability generating function of words with 2 occurrences of the pattern

> coeff(series(",u,3),u,2);

this gives rise to a linear recurrence satisfied by the Taylor coefficients

> diffeqtorec(y(z)-",y(z),u(n));

As before, in order to speed up the computation, we change the initial conditions into floating point numbers:

> Digits:=50:

> select(has,"",n) union {seq(op(1,i)=evalf(op(2,i)),i=remove(has,"",n))}:

gfun[rectoproc] then produces a procedure to evaluate this sequence efficiently

> p:=rectoproc(",u(n),remember):

> for i from 0 by 500 to 10000 do i,p(i) od;

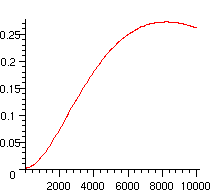
The following picture shows the evolution of this probability with the length of the word

> plot([seq([100*i,p(100*i)],i=0..100)]);

Extensions

Non uniform distribution

The bases A,C,G,T in DNA are not equiprobable. The combstruct model can be refined as follows to take into account such irregularities. We use here the values A=0.25, C=0.18, G=0.24, T=0.33 which come from a viral DNA ( X174). The pattern is the same as above. We only have to add marks in the grammar, compute a multivariate generating function and substitute the probabilities in it.

> G;

Marks are added by replacing a by Prod(Atom,Marka) everywhere it occurs, and similarly for the other letters. There Marka, Markb, Markc and Markd have size 0 and do not modify the counting sequences and the related probabilities, but make it possible to extract multivariate generating functions which contain more information.

> Gprob:=subs(a=Prod(Atom,Marka),b=Prod(Atom,Markb),c=Prod(Atom,Markc),d=Prod(Atom,Markd),G minus {a=Atom,b=Atom,c=Atom,d=Atom}) union {Marka=Epsilon, Markb=Epsilon, Markc=Epsilon, Markd=Epsilon};

Here is the multivariate generating function:

> gfsolve(Gprob,unlabelled,z,[[u,Mark],[a,Marka],[b,Markb],[c,Markc],[d,Markd]]);

> GF:=subs(",w(a,b,d,z,c,u));

The coefficient of in the Taylor expansion of GF in is the number of words of length with occurrences of the letter a, occurrences of the letter b ... and occurrences of the pattern. The probability generating function is obtained by substituting by the corresponding probability. Thus GF now takes into account both the specific pattern and the biased probabilities of the letters in the text.

We can again compute the probability that the pattern occurs twice in words of length and compare this with the uniform model:

> normal(coeff(series(GF,u,3),u,2));

Again we compute a linear recurrence satisfied by the Taylor coefficients from which we produce an efficient procedure for their evaluation:

> diffeqtorec(y(z)-",y(z),u(n)):

> nuprob:=rectoproc(subs([a=0.25,b=0.18,c=0.24,d=0.33],"),u(n),remember);

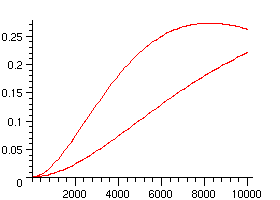
The probabilities for this non-uniform model are rather different from those obtained in the uniform model: the pattern abacab is now less probable, since b and c are less probable than in the uniform model.

> for i from 0 by 500 to 10000 do i,nuprob(i) od;

Here are the curves corresponding to the non-uniform and to the uniform model:

> plots[display]({plot([seq([100*i,p(100*i)],i=0..100)]),plot([seq([100*i,nuprob(100*i)],i=0..100)])});

Markovian model

By slightly modifying the automaton, it is possible to consider a Markovian model, where instead of giving the probabilities of occurrence of each letter, one gives the probabilities of transition from one letter to the next one. The new automaton is almost the same as the previous one, except that the transitions are marked and three more states are added at the begining. Here is the procedure generating the new automaton from the pattern:

> gengram2 := proc (pattern::list({identical(a), identical(b),identical(c), identical(d)}))local i, eq, letter, state, j,alph;alph:=[a,b,c,d];for i to nops(pattern) do for letter in alph do for j from 0 to i-1 do if [op(1 .. i-j,pattern)] =[op(j+1 .. i-1,pattern), letter] then state[letter] :=cat(w,op(1 .. i-j,pattern));break fi od;if j=i then state[letter] := cat(w,letter) fi od;eq[i] := cat(w,op(1 .. i-1,pattern)) =Union(Epsilon,seq(Prod(letter,`if`(i>1,cat(Mark,pattern[i-1],letter),cat(Markini,letter)),state[letter]), letter = alph))od;subs(cat(w,op(pattern)) =Prod(Mark,w),{Mark = Epsilon,seq(seq(cat(Mark,i,j)=Epsilon,j=alph),i=alph),seq(eq[i],i = 1 .. nops(pattern)),seq(letter = Atom,letter=alph), seq(cat(w,i)=Union(Epsilon,seq(Prod(j,cat(Mark,i,j),cat(w,j)),j=alph)),i=subs(pattern[1]=NULL,alph)),seq(cat(Markini,i)=Epsilon,i=alph)})end;

For instance, the same pattern abacab as above yields the automaton described by the following grammar

> G:=gengram2([a,b,a,c,a,b]);

From there, generating functions follow. For instance, we recover the generating function obtained before when all transitions are equiprobable:

> subs(gfsolve(G,unlabelled,z,[[u,Mark],seq([1/4,cat(Markini,i)],i=[a,b,c,d]),seq(seq([1/4,cat(Mark,i,j)],j=[a,b,c,d]),i=[a,b,c,d])]),w(z,u));

The rest of the treatment is as before.

Multiple patterns

It is also possible to write an automaton which will recognize not only a fixed pattern, but a set of possible patterns. The procedure gengram3 below takes as input a list of patterns, and produces the minimal grammar recognizing all words on 4 letters, the patterns being ``marked''.

> gengram3:=proc (patterns::list(list({identical(a),identical(b),identical(c),identical(d)}))) local alpha, states, state, eq, n, trans, letter, nbst, st, indst, i; alpha:=[a,b,c,d]; nbst:=1; states[1]:=[]; for indst while indst<=nbst do state:=states[indst]; n:=nops(state); for letter in alpha do if member([op(state),letter],patterns) then trans[letter]:=Prod(Mark,w) elif member([op(state),letter],map( proc(x,n) if nops(x)>n then [op(1..n+1,x)] fi end, patterns,nops(state))) then trans[letter]:=cat(w,op(state),letter); nbst:=nbst+1; states[nbst]:=[op(state),letter] else for i from indst by -1 to 2 do st:=states[i]; if st=[op(n-nops(st)+2..n,state),letter] then trans[letter]:=cat(w,op(st)); break fi od; if i=1 then trans[letter]:=w fi fi od; eq[indst]:=cat(w,op(state))= Union(Epsilon,seq(Prod(letter,trans[letter]),letter=alpha)) od; {seq(eq[i],i=1..nbst),Mark=Epsilon,seq(letter=Atom,letter=alpha)} end;

For instance, here is the grammar recognizing the words abab and abacab:

> G:=gengram3([[a,b,a,b],[a,b,a,c,a,b]]);

Again, generating functions follow:

> subs(gfsolve(G,unlabelled,z,[[u,Mark]]),w(z,u));

The coefficient of in the Taylor expansion of this rational function is the number of words of length with occurrences of the patterns abab and abacab. Here are the first few terms:

> map(expand,series(",z,10));

For instance the term corresponds to the 47 words of length 6 containing abab (ababab is counted only once), plus the word abacab itself. Of course, it would not be difficult to modify the grammar so as to take into accounts overlapping words differently. From this generating function, the treatment proceeds as before. Again, non-uniform and Markovian extensions could be considered.

Patterns with errors

It is also possible to accomodate patterns whose occurrence is exact except at one unspecified position. A direct way would be to apply the previous technique for multiple patterns after having generated all possible patterns obtained by introducing one error in the pattern under study. However, the number of patterns obtained this way may be much too large for this technique to be practical. A better way is to produce directly the automaton corresponding to occurrences of the pattern with at most one error, and this turns out not to be too difficult. The following procedure generates all words of length , exact occurrences of the pattern being tagged with a mark as before (Mark0err), while occurrences with one mismatch are tagged by a Mark1err mark.

> gengram4:=proc (pattern::list({identical(a),identical(b),identical(c),identical(d)})) local alpha, state, eq, n, letter, st, i, eq2, staterr, j; alpha:=[a,b,c,d]; for i to nops(pattern) do staterr[i]:={}; for letter in alpha do for j from 0 to i do if j=i or [op(1 .. i - j, pattern)] = [op(j + 1 .. i - 1, pattern), letter] then if j=0 then state[letter] := cat(w, op(1 .. i , pattern)) else staterr[i]:=staterr[i] union {[[op(1..i,pattern)], [op(1..i-j,pattern)]]}; state[letter]:=cat(w,op(1..i,pattern),`|`, op(1..i-j,pattern)) fi; break fi od; od; eq[i] := cat(w, op(1 .. i - 1, pattern)) = Union(Epsilon, seq(Prod(letter, state[letter]), letter = alpha)) od; for i to nops(pattern)-1 do for st in staterr[i] do n:=nops(st[2]); for letter in alpha do for j from 0 to n+1 do if j=n+1 or [op(1..n-j+1,pattern)]= [op(j+1..n,st[2]),letter] then if pattern[i+1]=letter then state[letter]:=cat(w,op(1..i+1,pattern),`|`, op(1..n-j+1,pattern)); staterr[i+1]:=staterr[i+1] union {[[op(1..i+1,pattern)],[op(1..n-j+1,pattern)]]} else state[letter]:=cat(w,op(1..n-j+1,pattern)) fi; break fi od od; eq2[st] := cat(w,op(st[1]),`|`,op(st[2])) = Union(Epsilon, seq(Prod(letter, state[letter]), letter = alpha)) od od; {seq(eq[i],i=1..nops(pattern)), seq(seq(eq2[st],st=staterr[i]),i=1..nops(pattern)-1), cat(w,op(pattern))=Prod(Mark0err,w), seq(cat(w,op(st[1]),`|`,op(st[2]))=Prod(Mark1err,w), st=staterr[nops(pattern)]), Mark0err=Epsilon,Mark1err=Epsilon,seq(letter=Atom,letter=alpha)} end;

Here is a simple example. The generated automaton is almost optimal (in general it has O(1) too many states):

> gengram4([a,b,b,c]);

There are two kinds of states: states corresponding to words without error, which as before are represented by w.prefix, and states with one error which contain a `|', possibly followed by the last few letters which were read, when these form a prefix of the pattern. For instance, wabb|ab is the state reached by words which contain the string abb with one error, their last two letters being ab.
From there, we derive trivariate generating functions:

> subs(gfsolve(",unlabelled,z,[[u,Mark0err],[v,Mark1err]]),w(z,u,v));

The coefficient of in the Taylor expansion of this rational function at is the number or words of length where the pattern abbc occurs times without error and times with exactly one error. Again, the Markovian model could also be treated, and extensions to multiple errors are likely to be possible as well.

>

Conclusion

Various probabilistic parameters related to the occurrence of specific patterns in random words can be computed very easily using combstruct and gfun. Here, combstruct is used to model the combinatorics of the problem and gfun is very helpful to compute expansions to very large orders, thanks to the rational type of the corresponding generating functions. The model itself can be modified in various directions, to take into account different probability models or different ways of counting occurrences of the pattern when they overlap, or several patterns simultaneously.