An Algolib-aided Version of Apery's Proof of the Irrationality of zeta(3)

Bruno Salvy

(March 4, 2003)

Apery proved in 1978 that 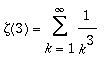zeta(3) = Sum(1/(k^3),k = 1 .. infinity)  is irrational. We give a short version of Apery's proof that uses several tools from Algolib: gfun, Mgfun and equivalent. We only prove irrationality here and do not compute irrationality measures.

The starting point is the definition of three sequences:

>    c[n,k]:=binomial(n,k)^2*binomial(n+k,k)^2;

c[n,k] := binomial(n,k)^2*binomial(n+k,k)^2

>    a[n]:=Sum(c[n,k],k=0..n);

a[n] := Sum(binomial(n,k)^2*binomial(n+k,k)^2,k = 0 .. n)

>    b[n]:='a[n]'*Sum(1/k^3,k=1..n)+Sum(Sum((-1)^(m+1)*c[n,k]/2/m^3/binomial(n,m)/binomial(n+m,m),m=1..k),k=1..n);

b[n] := a[n]*Sum(1/(k^3),k = 1 .. n)+Sum(Sum(1/2*(-1)^(m+1)*binomial(n,k)^2*binomial(n+k,k)^2/m^3/binomial(n,m)/binomial(n+m,m),m = 1 .. k),k = 1 .. n)

1. limit(b[n]/a[n],n = infinity) = zeta(3)

The first part of the right-hand side of the definition of b[n]  provides the desired limit for b[n] / a[n] . The proof consists in showing that the second part tends to 0, when divided by a[n] . Let

>    U:=m^3*binomial(n,m)*binomial(n+m,m);

U := m^3*binomial(n,m)*binomial(n+m,m)

What we are going to show is that n^2 <= U . Thus the second sum in b[n]  is bounded by Sum(Sum(c[n,k]/2/(n^2),m = 1 .. k),k = 1 .. n) <= Sum(k*c[n,k]/2/(n^2),k = 1 .. n) , itself bounded by a[n]/(2*n) , whence the desired limit.

The following simple way of proving this was suggested to us by Philippe Dumas:

For m=n, we have the desired inequality:

>    eval(U,m=n);

n^3*binomial(2*n,n)

Otherwise, we have that binomial(n,m) <= binomial(n+m,m) , and the conclusion follows since for m  between 1 and n-1 , one has n <= binomial(n,m) .

2. a[n]  is a positive integer and d[n]^3*b[n]  is an integer, where d[n]  is the lcm of 1,..., n

The first assertion comes from binomials being integers.

The second one is obtained by showing that each summand in the double sum defining b[n]  has a denominator dividing d[k] . This is done in two steps as follows:

>    (binomial(n,k)^2*binomial(n+k,k)^2/m^3/binomial(n,m)/binomial(n+m,m))=binomial(n,k)*binomial(n+k,k)*binomial(n-m,n-k)*binomial(n+k,k-m)/m^3/binomial(k,m)^2;

binomial(n,k)^2*binomial(n+k,k)^2/m^3/binomial(n,m)/binomial(n+m,m) = binomial(n,k)*binomial(n+k,k)*binomial(n-m,n-k)*binomial(n+k,k-m)/m^3/binomial(k,m)^2

Proof:

>    convert(lhs(%)/rhs(%),GAMMA);

1

and then it is sufficient to observe that m*binomial(k,m)  divides d[k] .

3. Both a[n]  and b[n]  satisfy a simple linear recurrence

This is where the Mgfun  package will be useful.

Recurrence satisfied by a[n]

>    CT:=Mgfun[creative_telescoping](c[n,k],n::shift,k::shift);

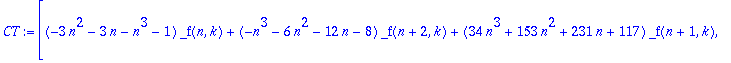
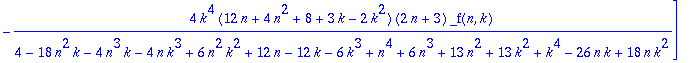
CT := [(-3*n^2-3*n-n^3-1)*_f(n,k)+(-n^3-6*n^2-12*n-8)*_f(n+2,k)+(34*n^3+153*n^2+231*n+117)*_f(n+1,k), -4*k^4*(12*n+4*n^2+8+3*k-2*k^2)*(2*n+3)/(4-18*n^2*k-4*n^3*k-4*n*k^3+6*n^2*k^2+12*n-12*k-6*k^3+n^4+6...
CT := [(-3*n^2-3*n-n^3-1)*_f(n,k)+(-n^3-6*n^2-12*n-8)*_f(n+2,k)+(34*n^3+153*n^2+231*n+117)*_f(n+1,k), -4*k^4*(12*n+4*n^2+8+3*k-2*k^2)*(2*n+3)/(4-18*n^2*k-4*n^3*k-4*n*k^3+6*n^2*k^2+12*n-12*k-6*k^3+n^4+6...

This result means that applying the recurrence operator given by the first element of this list to   c[n,k] , one gets the difference g(n,k)-g(n,k+1) , where g  is the second element of this list. Explicitly,

>    eval(CT[1],_f=proc(N,K) 'c[N,K]' end)=g(n,k)-g(n,k+1);

(-3*n^2-3*n-n^3-1)*c[n,k]+(-n^3-6*n^2-12*n-8)*c[n+2,k]+(34*n^3+153*n^2+231*n+117)*c[n+1,k] = g(n,k)-g(n,k+1)

with

>    g(n,k)=subs(_f(n,k)='c[n,k]',CT[2]);

g(n,k) = -4*k^4*(12*n+4*n^2+8+3*k-2*k^2)*(2*n+3)/(4-18*n^2*k-4*n^3*k-4*n*k^3+6*n^2*k^2+12*n-12*k-6*k^3+n^4+6*n^3+13*n^2+13*k^2+k^4-26*n*k+18*n*k^2)*c[n,k]

We check this formula by computing the ratio left-hand side divided by right-hand side:

>    ct:=eval(CT,_f=unapply(c[n,k],n,k)):

>    normal(expand(ct[1]/(ct[2]-subs(k=k+1,ct[2]))));

1

Now, summing this identity for k  from 0 to n +2, we get that the right-hand side telescopes, leaving out g(n,0)-g(n,n+3) . This in turn is 0:

>    eval(ct[2],k=0);

0

>    normal(limit(ct[2],k=n+3));

0

The sequence c[n,k]  is 0 for k = n+1  and k = n+2 , and thus its sum up to k = n+2  is equal to a[n] .

Thus we have proved that the sequence a[n]  satisfies the following recurrence (with A = a )

>    collect(eval(CT[1],_f=proc(n,k) A(n) end),A,factor)=0;

-(n+1)^3*A(n)-(n+2)^3*A(n+2)+(2*n+3)*(17*n^2+51*n+39)*A(n+1) = 0

>    rec:=op(1,%):

We check this recurrence by computing the first few values of a[n] :

>    lista:=[seq(value(subs(n=i,a[n])),i=1..20)];

lista := [5, 73, 1445, 33001, 819005, 21460825, 584307365, 16367912425, 468690849005, 13657436403073, 403676083788125, 12073365010564729, 364713572395983725, 11111571997143198073, 341034504521827105445...
lista := [5, 73, 1445, 33001, 819005, 21460825, 584307365, 16367912425, 468690849005, 13657436403073, 403676083788125, 12073365010564729, 364713572395983725, 11111571997143198073, 341034504521827105445...
lista := [5, 73, 1445, 33001, 819005, 21460825, 584307365, 16367912425, 468690849005, 13657436403073, 403676083788125, 12073365010564729, 364713572395983725, 11111571997143198073, 341034504521827105445...

and then substituting these in the left-hand side of the recurrence:

>    seq(eval(rec,[n=i,A=proc(k) lista[k] end]),i=1..18);

0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0

Recurrence satisfied by b[n]

First, we observe that the recurrence above seems to be satisfied by the sequence b[n] :

>    for i to 10 do listb[i]:=lista[i]*add(1/k^3,k=1..i)+add(binomial(i,k)^2*binomial(i+k,k)^2/2*add((-1)^(m-1)/m^3/binomial(i,m)/binomial(i+m,m),m=1..k),k=1..i) od:

>    seq(eval(rec,[n=i,A=proc(k) listb[k] end]),i=2..7);

0, 0, 0, 0, 0, 0

In order to get a proof  that the recurrence is actually satisfied by b[n] , we use a similar process based on creative telescoping. The situation is slightly more complicated, since it is necessary to obtain a system of recurrences satisfied by the summand first.

Indefinite sum inside b[n]

We start with the inner summand, for the indefinite sum of which we need to find description making creative telescoping possible:

>    d[n,m]:=(-1)^(m+1)/2/m^3/binomial(n,m)/binomial(n+m,m);

d[n,m] := 1/2*(-1)^(m+1)/m^3/binomial(n,m)/binomial(n+m,m)

We first get operators by definition of the indefinite sum:

>    Mgfun[dfinite_expr_to_sys](d[n,m],f(n::shift,m::shift));

{(-n+m-1)*f(n,m)+(n+m+1)*f(n+1,m), m^3*f(n,m)+(m*n^2+n^2+m*n+n-2*m^2-m^3-m)*f(n,m+1)}

>    firstoperators:=subs(k=k+1,subs(m=k,eval(%,f=proc(n,m) g(n,m)-g(n,m-1) end)));

firstoperators := {(k+1)^3*(g(n,k+1)-g(n,k))+(n^2*(k+1)+n^2+n*(k+1)+n-2*(k+1)^2-(k+1)^3-k-1)*(g(n,2+k)-g(n,k+1)), (-n+k)*(g(n,k+1)-g(n,k))+(n+2+k)*(g(n+1,k+1)-g(n+1,k))}
firstoperators := {(k+1)^3*(g(n,k+1)-g(n,k))+(n^2*(k+1)+n^2+n*(k+1)+n-2*(k+1)^2-(k+1)^3-k-1)*(g(n,2+k)-g(n,k+1)), (-n+k)*(g(n,k+1)-g(n,k))+(n+2+k)*(g(n+1,k+1)-g(n+1,k))}
firstoperators := {(k+1)^3*(g(n,k+1)-g(n,k))+(n^2*(k+1)+n^2+n*(k+1)+n-2*(k+1)^2-(k+1)^3-k-1)*(g(n,2+k)-g(n,k+1)), (-n+k)*(g(n,k+1)-g(n,k))+(n+2+k)*(g(n+1,k+1)-g(n+1,k))}

We check that these operators cancel our sequence when evaluated at a special point (here n = 10, k = 6 ):

>    eval(firstoperators,g=proc(N,K) Sum(subs(n=N,d[n,m]),m=1..K) end):

>    eval(%,n=10):

>    value(subs(k=6,%));

{0}

These operators do not generate a D-finite ideal

In order to ensure the success of creative telescoping, we need to compute "sufficiently many" operators annihilating our sequence. This "sufficiently many" is formally defined in terms of the dimension of the ideal our operators generate. A D-finite ideal is an ideal such that the quotient of the algebra of operators with the ideal is finitely dimensional as a vector space. Informally, this amounts to saying that all the shifts of a sequence annihilated by the operators can be rewritten as linear combination of a finite number of them. Technically, D-finiteness can be checked by computing the Hilbert dimension of the ideal, which has to be 0.

>    sys:=subs([seq(seq(g(n+i,k+j)=Sn^i*Sk^j,j=0..2),i=0..1)],firstoperators);

sys := {(-n+k)*(Sk-1)+(n+2+k)*(Sn*Sk-Sn), (k+1)^3*(Sk-1)+(n^2*(k+1)+n^2+n*(k+1)+n-2*(k+1)^2-(k+1)^3-k-1)*(Sk^2-Sk)}
sys := {(-n+k)*(Sk-1)+(n+2+k)*(Sn*Sk-Sn), (k+1)^3*(Sk-1)+(n^2*(k+1)+n^2+n*(k+1)+n-2*(k+1)^2-(k+1)^3-k-1)*(Sk^2-Sk)}

>    Groebner[hilbertdim](sys,Groebner[termorder](Ore_algebra[shift_algebra]([Sn,n],[Sk,k]),tdeg(Sn,Sk)));

1

This would be zero in the case of a D-finite system.

More generators are obtained by creative telescoping:

>    CT2:=Mgfun[creative_telescoping](d[n,m],n::shift,m::shift);

CT2 := [-_f(n,m)+_f(n+1,m), -2*m*(n-m+1)/(n^2+2*n+1)*_f(n,m)]

Then, in order to sum d[n,m]  for m from 1 to k, we first find annihilators of the right-hand side:

>    Mgfun[dfinite_expr_to_sys](subs(_f(n,m)=d[n,m],m=k+1,CT2[2])-subs(_f(n,m)=d[n,m],m=1,CT2[2]),f(n::shift,k::shift));

{(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*f(n,k)+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*f(n+2,k)+(-112+2*n^3*k+24*n*k+12*n^2*k-4...
{(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*f(n,k)+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*f(n+2,k)+(-112+2*n^3*k+24*n*k+12*n^2*k-4...
{(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*f(n,k)+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*f(n+2,k)+(-112+2*n^3*k+24*n*k+12*n^2*k-4...
{(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*f(n,k)+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*f(n+2,k)+(-112+2*n^3*k+24*n*k+12*n^2*k-4...

and then we get annihilators for the indefinite sum by substitution in the left-hand side:

>    ann:=eval(%,f=proc(N,K) unapply(CT2[1],n,m)(N,K) end);

ann := {(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*(-_f(n,k)+_f(n+1,k))+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*(-_f(n+2,k)+_f(n+3,...
ann := {(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*(-_f(n,k)+_f(n+1,k))+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*(-_f(n+2,k)+_f(n+3,...
ann := {(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*(-_f(n,k)+_f(n+1,k))+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*(-_f(n+2,k)+_f(n+3,...
ann := {(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*(-_f(n,k)+_f(n+1,k))+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*(-_f(n+2,k)+_f(n+3,...
ann := {(5-21*n^2*k-11*n^3*k+13*n^4+32*n^3+22*n-5*k-17*n*k+38*n^2+2*n^5-2*n^4*k)*(-_f(n,k)+_f(n+1,k))+(2*n^5+27*n^4+2*n^4*k+21*n^3*k+144*n^3+378*n^2+81*n^2*k+135*n*k+486*n+243+81*k)*(-_f(n+2,k)+_f(n+3,...

Again, we check that these operators are correct at n = 10, k = 6 :

>    eval(ann,_f=proc(N,K) Sum(subs(n=N,d[n,m]),m=1..K) end):

>    subs(n=10,%):

>    value(subs(k=6,%));

{0}

Finally, we put both sets of generators together:

>    ann2:=map(collect,ann union subs(g=_f,firstoperators),_f,factor);

ann2 := {-(n+2)^3*_f(n+2,k)+(2*n+3)*(n^2-n*k+3*n+k^2+3)*_f(n+1,k)+(-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1)*_f(n,k)+k*(2*n+3)*(n-k)*_f(n+1,k+1)-k*(2*n+3)*(n-k)*_f(n,k+1), -(k+1)^3*_f(n,k)+(2*k^3+8...
ann2 := {-(n+2)^3*_f(n+2,k)+(2*n+3)*(n^2-n*k+3*n+k^2+3)*_f(n+1,k)+(-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1)*_f(n,k)+k*(2*n+3)*(n-k)*_f(n+1,k+1)-k*(2*n+3)*(n-k)*_f(n,k+1), -(k+1)^3*_f(n,k)+(2*k^3+8...
ann2 := {-(n+2)^3*_f(n+2,k)+(2*n+3)*(n^2-n*k+3*n+k^2+3)*_f(n+1,k)+(-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1)*_f(n,k)+k*(2*n+3)*(n-k)*_f(n+1,k+1)-k*(2*n+3)*(n-k)*_f(n,k+1), -(k+1)^3*_f(n,k)+(2*k^3+8...
ann2 := {-(n+2)^3*_f(n+2,k)+(2*n+3)*(n^2-n*k+3*n+k^2+3)*_f(n+1,k)+(-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1)*_f(n,k)+k*(2*n+3)*(n-k)*_f(n+1,k+1)-k*(2*n+3)*(n-k)*_f(n,k+1), -(k+1)^3*_f(n,k)+(2*k^3+8...
ann2 := {-(n+2)^3*_f(n+2,k)+(2*n+3)*(n^2-n*k+3*n+k^2+3)*_f(n+1,k)+(-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1)*_f(n,k)+k*(2*n+3)*(n-k)*_f(n+1,k+1)-k*(2*n+3)*(n-k)*_f(n,k+1), -(k+1)^3*_f(n,k)+(2*k^3+8...
ann2 := {-(n+2)^3*_f(n+2,k)+(2*n+3)*(n^2-n*k+3*n+k^2+3)*_f(n+1,k)+(-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1)*_f(n,k)+k*(2*n+3)*(n-k)*_f(n+1,k+1)-k*(2*n+3)*(n-k)*_f(n,k+1), -(k+1)^3*_f(n,k)+(2*k^3+8...

Now, this is D-finite

>    sys:=subs([seq(seq(_f(n+i,k+j)=Sn^i*Sk^j,j=0..2),i=0..3)],ann2);

sys := {-(k+1)^3+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*Sk+(2+k)*(n+2+k)*(n-k-1)*Sk^2, -(n+2)^3*Sn^2+(2*n+3)*(n^2-n*k+3*n+k^2+3)*Sn-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1+k*(2*n+3)*(n-k)*Sn*Sk-k...
sys := {-(k+1)^3+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*Sk+(2+k)*(n+2+k)*(n-k-1)*Sk^2, -(n+2)^3*Sn^2+(2*n+3)*(n^2-n*k+3*n+k^2+3)*Sn-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1+k*(2*n+3)*(n-k)*Sn*Sk-k...
sys := {-(k+1)^3+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*Sk+(2+k)*(n+2+k)*(n-k-1)*Sk^2, -(n+2)^3*Sn^2+(2*n+3)*(n^2-n*k+3*n+k^2+3)*Sn-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1+k*(2*n+3)*(n-k)*Sn*Sk-k...
sys := {-(k+1)^3+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*Sk+(2+k)*(n+2+k)*(n-k-1)*Sk^2, -(n+2)^3*Sn^2+(2*n+3)*(n^2-n*k+3*n+k^2+3)*Sn-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1+k*(2*n+3)*(n-k)*Sn*Sk-k...
sys := {-(k+1)^3+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*Sk+(2+k)*(n+2+k)*(n-k-1)*Sk^2, -(n+2)^3*Sn^2+(2*n+3)*(n^2-n*k+3*n+k^2+3)*Sn-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1+k*(2*n+3)*(n-k)*Sn*Sk-k...
sys := {-(k+1)^3+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*Sk+(2+k)*(n+2+k)*(n-k-1)*Sk^2, -(n+2)^3*Sn^2+(2*n+3)*(n^2-n*k+3*n+k^2+3)*Sn-3*k^2-n^3+2*n^2*k-3*n^2+3*n*k-2*n*k^2-3*n-1+k*(2*n+3)*(n-k)*Sn*Sk-k...

>    Groebner[hilbertdim](sys,Groebner[termorder](Ore_algebra[shift_algebra]([Sn,n],[Sk,k]),tdeg(Sn,Sk)));

0

Building up the summand

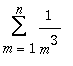From the (D-finite) system of operators annihilating the indefinite sum of d[n,m] , we are now going to construct a system of operators annihilating the summand in b[n] , before applying creative telescoping. This last step will be possible because addition and product of D-finite systems remain D-finite. Thus we now add Sum(1/(m^3),m = 1 .. n)  and multiply by c[n,k] . This is achieved by first constructing a system annihilating the sum:

>    inhom:=(n+1)^3*(_f(n+1,k)-_f(n,k))-1;

inhom := (n+1)^3*(-_f(n,k)+_f(n+1,k))-1

(the system is composed of this equation, which we render homogeneous, and another one reflecting that the sum does not depend on k ). Then we construct the system satisfied by the sum:

>    Mgfun[`sys+sys`]({_f(n,k+1)-_f(n,k),subs(n=n+1,inhom)-inhom},ann2);

{(-n-2-k)*_f(n+1,k)+(n-k)*_f(n,k)+(-n+k)*_f(n,k+1)+(n+2+k)*_f(n+1,k+1), (-k^3-3*k^2-3*k-1)*_f(n,k)+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*_f(n,k+1)+(2*n^2+n*k+2*n-8*k-4-5*k^2+n^2*k-k^3)*_f(n,2+k), (2...
{(-n-2-k)*_f(n+1,k)+(n-k)*_f(n,k)+(-n+k)*_f(n,k+1)+(n+2+k)*_f(n+1,k+1), (-k^3-3*k^2-3*k-1)*_f(n,k)+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*_f(n,k+1)+(2*n^2+n*k+2*n-8*k-4-5*k^2+n^2*k-k^3)*_f(n,2+k), (2...
{(-n-2-k)*_f(n+1,k)+(n-k)*_f(n,k)+(-n+k)*_f(n,k+1)+(n+2+k)*_f(n+1,k+1), (-k^3-3*k^2-3*k-1)*_f(n,k)+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*_f(n,k+1)+(2*n^2+n*k+2*n-8*k-4-5*k^2+n^2*k-k^3)*_f(n,2+k), (2...
{(-n-2-k)*_f(n+1,k)+(n-k)*_f(n,k)+(-n+k)*_f(n,k+1)+(n+2+k)*_f(n+1,k+1), (-k^3-3*k^2-3*k-1)*_f(n,k)+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*_f(n,k+1)+(2*n^2+n*k+2*n-8*k-4-5*k^2+n^2*k-k^3)*_f(n,2+k), (2...
{(-n-2-k)*_f(n+1,k)+(n-k)*_f(n,k)+(-n+k)*_f(n,k+1)+(n+2+k)*_f(n+1,k+1), (-k^3-3*k^2-3*k-1)*_f(n,k)+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*_f(n,k+1)+(2*n^2+n*k+2*n-8*k-4-5*k^2+n^2*k-k^3)*_f(n,2+k), (2...
{(-n-2-k)*_f(n+1,k)+(n-k)*_f(n,k)+(-n+k)*_f(n,k+1)+(n+2+k)*_f(n+1,k+1), (-k^3-3*k^2-3*k-1)*_f(n,k)+(2*k^3+8*k^2+11*k+5-n^2*k-2*n^2-n*k-2*n)*_f(n,k+1)+(2*n^2+n*k+2*n-8*k-4-5*k^2+n^2*k-k^3)*_f(n,2+k), (2...

and similarly we multiply by c[n,k] :

>    Mgfun[`sys*sys`](%,Mgfun[dfinite_expr_to_sys](c[n,k],_f(n::shift,k::shift)));

{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...
{(-11*n^2*k-55*k^5+9*n^3*k-5*n*k^3-30*k^6-6*k^7+53*n^2*k^4-41*n^2*k^2-45*k^5*n+17*n^6*k-6*n^5*k^3-2*n^6*k^2-20*n^5*k^2-16*k^3*n^4+4*n-4*k+3*n^7*k-25*k^3+n^8+9*n^7+85*n^4+61*n^3+24*n^2-12*k^2-48*k^4-12*...

Creative telescoping

This is the time-consuming part of this worksheet: we now compute a recurrence satisfied by b[n]  by applying creative telescoping to the summand defined by the system we have just computed.

The following instruction triggers the display of extra information during the computation:

>    infolevel[Mgfun]:=5:

>    res:=Mgfun[creative_telescoping](LFSol(%%),n::shift,k::shift); 

Mgfun/chyzak97:   "Suitable term order guessed"

Mgfun/chyzak97:   "Implicit d-finite expression recognized"

Mgfun/chyzak97:   "Dimension is 3"

Mgfun/chyzak97:   "Start of Chyzak's algorithm"

Mgfun/chyzak97:   "Preparation of the system: .60e-1 seconds."

Mgfun/uncoupling:   "Uncoupling of the LOF system"

Mgfun/chyzak97:   "Uncoupling of the system: 1.011 seconds."

Mgfun/rational_sys_solve:   "Look for rational solutions of a system"

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .11e-1 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .20e-1 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 1"

Mgfun/rational_sys_solve:   "Solving equation: .580 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 2"

Mgfun/rational_sys_solve:   "Solving equation: .10e-1 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 3"

Mgfun/rational_sys_solve:   "Solving equation: 0. seconds."

Mgfun/chyzak97:   "No LOFE of order 0 :-("

Mgfun/chyzak97:   "Preparation of the system: .70e-1 seconds."

Mgfun/uncoupling:   "Uncoupling of the LOF system"

Mgfun/chyzak97:   "Uncoupling of the system: 1.160 seconds."

Mgfun/rational_sys_solve:   "Look for rational solutions of a system"

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .19e-1 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .39e-1 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 1"

Mgfun/rational_sys_solve:   "Solving equation: 1.210 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 2"

Mgfun/rational_sys_solve:   "Solving equation: 0. seconds."

Mgfun/rational_sys_solve:   "Equations solved: 3"

Mgfun/rational_sys_solve:   "Solving equation: 0. seconds."

Mgfun/chyzak97:   "No LOFE of order 1 :-("

Mgfun/chyzak97:   "Preparation of the system: .350 seconds."

Mgfun/uncoupling:   "Uncoupling of the LOF system"

Mgfun/chyzak97:   "Uncoupling of the system: 3.360 seconds."

Mgfun/rational_sys_solve:   "Look for rational solutions of a system"

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .60e-1 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .119 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 1"

Mgfun/rational_sys_solve:   "Solving equation: 9.260 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 2"

Mgfun/rational_sys_solve:   "Solving equation: .10e-1 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 3"

Mgfun/rational_sys_solve:   "Solving equation: 0. seconds."

Mgfun/chyzak97:   "No LOFE of order 2 :-("

Mgfun/chyzak97:   "Preparation of the system: .869 seconds."

Mgfun/uncoupling:   "Uncoupling of the LOF system"

Mgfun/chyzak97:   "Uncoupling of the system: 2.831 seconds."

Mgfun/rational_sys_solve:   "Look for rational solutions of a system"

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .11e-1 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .11e-1 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 1"

Mgfun/rational_sys_solve:   "Solving equation: 46.491 seconds."

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .401 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .511 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 2"

Mgfun/rational_sys_solve:   "Solving equation: 4.259 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 3"

Mgfun/rational_sys_solve:   "Solving equation: 0. seconds."

Mgfun/chyzak97:   "No LOFE of order 3 :-("

Mgfun/chyzak97:   "Preparation of the system: 1.980 seconds."

Mgfun/uncoupling:   "Uncoupling of the LOF system"

Mgfun/chyzak97:   "Uncoupling of the system: 6.250 seconds."

Mgfun/rational_sys_solve:   "Look for rational solutions of a system"

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .120 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .131 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 1"

Mgfun/rational_sys_solve:   "Solving equation: 584.509 seconds."

`Mgfun/denominator_bound`[shift]   "Intermediate bound on dispersion: infinity"

`Mgfun/denominator_bound`[shift]   "Bound on dispersion: 0"

`Mgfun/denominator_bound`[shift]   "Computing a resultant: .609 seconds."

`Mgfun/rational_solve`[shift]   "Computing denominator bound: .900 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 2"

Mgfun/rational_sys_solve:   "Solving equation: 5801.681 seconds."

Mgfun/rational_sys_solve:   "Equations solved: 3"

Mgfun/rational_sys_solve:   "Solving equation: 479.559 seconds."

Mgfun/chyzak97:   "LOFE of order 4 found!"

res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...
res := [(24*n^11+516*n^10+4886*n^9+26857*n^8+95126*n^7+227903*n^6+377072*n^5+431431*n^4+335182*n^3+168781*n^2+49694*n+6496)*_f(n,k)+(-39984*n^10-36186406*n-124475130*n^3-6838944-118568383*n^4-78684854*...

b[n]  satisfies the same recurrence as a[n]

As we did for a[n] , we now sum this for k from 0 to n+4 and we observe the following:

The right-hand side telescopes to 0

>    R:=res[2]:

>    eval(R,k=0);

0

>    F:=c[n,k]*(Sum(1/m^3,m=1..n)+Sum(d[n,m],m=1..k));

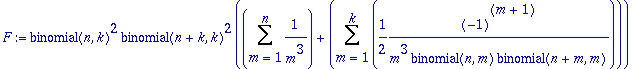
F := binomial(n,k)^2*binomial(n+k,k)^2*(Sum(1/(m^3),m = 1 .. n)+Sum(1/2*(-1)^(m+1)/m^3/binomial(n,m)/binomial(n+m,m),m = 1 .. k))

>    ff:=eval(R,_f=proc(N,K) subs(n=N,k=K,F) end):

>    expand(eval(ff,k=n+5));

0

Thus, we have found the following 4th order recurrence satisfied by b[n] :

>    eval(collect(res[1],_f,factor),_f=proc(n,k) A(n) end);

(2*n+5)*(13896*n^10+347400*n^9+3868998*n^8+25269960*n^7+107159724*n^6+308199360*n^5+608681313*n^4+814935630*n^3+707785777*n^2+360083510*n+81495208)*A(n+2)-(2*n+3)*(2*n+7)*(408*n^9+7956*n^8+68086*n^7+33...
(2*n+5)*(13896*n^10+347400*n^9+3868998*n^8+25269960*n^7+107159724*n^6+308199360*n^5+608681313*n^4+814935630*n^3+707785777*n^2+360083510*n+81495208)*A(n+2)-(2*n+3)*(2*n+7)*(408*n^9+7956*n^8+68086*n^7+33...
(2*n+5)*(13896*n^10+347400*n^9+3868998*n^8+25269960*n^7+107159724*n^6+308199360*n^5+608681313*n^4+814935630*n^3+707785777*n^2+360083510*n+81495208)*A(n+2)-(2*n+3)*(2*n+7)*(408*n^9+7956*n^8+68086*n^7+33...
(2*n+5)*(13896*n^10+347400*n^9+3868998*n^8+25269960*n^7+107159724*n^6+308199360*n^5+608681313*n^4+814935630*n^3+707785777*n^2+360083510*n+81495208)*A(n+2)-(2*n+3)*(2*n+7)*(408*n^9+7956*n^8+68086*n^7+33...
(2*n+5)*(13896*n^10+347400*n^9+3868998*n^8+25269960*n^7+107159724*n^6+308199360*n^5+608681313*n^4+814935630*n^3+707785777*n^2+360083510*n+81495208)*A(n+2)-(2*n+3)*(2*n+7)*(408*n^9+7956*n^8+68086*n^7+33...
(2*n+5)*(13896*n^10+347400*n^9+3868998*n^8+25269960*n^7+107159724*n^6+308199360*n^5+608681313*n^4+814935630*n^3+707785777*n^2+360083510*n+81495208)*A(n+2)-(2*n+3)*(2*n+7)*(408*n^9+7956*n^8+68086*n^7+33...

>    rec2:=%:

Check:

>    seq(eval(subs(n=i,rec2),A=proc(n) listb[n] end),i=1..6);

0, 0, 0, 0, 0, 0

Now, we observe using gfun   that all solutions of the second order recurrence rec found above to be satisfied by a[n]  are also solutions of this recurrence:

>    expand(gfun[`rec+rec`](rec,rec2,A(n))-rec2);

0

This shows that rec2 is also satisfied by all linear combinations of solutions of rec and rec2.

Therefore, to prove that b[n]  satisfies rec, it is sufficient to check that its first 4 values satisfy it, which has been done above.

4. Asymptotic behaviour of c[n] := a[n]*zeta(3)-b[n]

We start from the recurrence satisfied by a[n] , b[n]  and c[n]  defined in the title of this section:

>    rec;

-(n+1)^3*A(n)-(n+2)^3*A(n+2)+(2*n+3)*(17*n^2+51*n+39)*A(n+1)

and consider the differential equation satisfied by generating functions of its solutions

>    gfun[rectodiffeq](rec,A(n),y(z));

{y(0) = _C[0], D(y)(0) = _C[1], (-z+5)*y(z)+(-7*z^2+112*z-1)*diff(y(z),z)+(-6*z^3+153*z^2-3*z)*diff(y(z),`$`(z,2))+(-z^4+34*z^3-z^2)*diff(y(z),`$`(z,3))-5*_C[0]+_C[1]}
{y(0) = _C[0], D(y)(0) = _C[1], (-z+5)*y(z)+(-7*z^2+112*z-1)*diff(y(z),z)+(-6*z^3+153*z^2-3*z)*diff(y(z),`$`(z,2))+(-z^4+34*z^3-z^2)*diff(y(z),`$`(z,3))-5*_C[0]+_C[1]}

we make this homogeneous:

>    deq:=collect(gfun[diffeqtohomdiffeq](op(remove(type,%,`=`)),y(z))/(5*_C[0]-_C[1]),diff,factor);

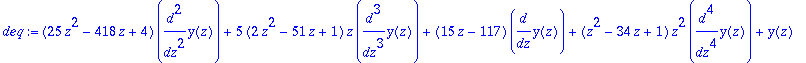
deq := (25*z^2-418*z+4)*diff(y(z),`$`(z,2))+5*(2*z^2-51*z+1)*z*diff(y(z),`$`(z,3))+(15*z-117)*diff(y(z),z)+(z^2-34*z+1)*z^2*diff(y(z),`$`(z,4))+y(z)

The solutions of this equation (and therefore the generating functions A(z) , B(z)  and C(z)  of the sequences a[n] , b[n]  and c[n] ) may have singularities only at 0, infinity , and any of the roots of the leading coefficient of this equation:

>    polsing:=coeff(deq,diff(y(z),[z$4]))/z^2;

polsing := z^2-34*z+1

Here are the roots of this polynomial

>    solve(polsing,z);

17+12*2^(1/2), 17-12*2^(1/2)

and the corresponding numerical values

>    evalf([%]);

[33.97056274, .2943726e-1]

First, it should be observed (by simple bounds on the binomial coefficients) that the sequences do not grow so fast as to make their generating series divergent. Therefore 0 is not a singularity of the functions we're interested in. Secondly, the sequence a[n]  is clearly increasing, which implies that A(z)  has a singularity of modulus smaller than 1, which has to be alpha = 17-12*sqrt(2) . Since b[n] / a[n]  has a finite limit, this is also a singularity of B(z) . A crucial step of the proof is to observe that C(z)  is not  singular at that point and therefore its singularity of smallest modulus is 1/ alpha = 17+12*sqrt(2) , whence an exponential growth of c[n]   in alpha^n . This step is achieved by considering the local behaviour of the solutions of the differential equation at alpha :

>    alias(alpha=RootOf(polsing)):DEtools[formal_sol](deq,y(z),T,z=alpha,terms=4);

[[series(1/2+(-54119/2880+1591/2880*alpha)*T+(138391/224-26189/1440*alpha)*T^2+(-8270626649/453600+486929033/907200*alpha)*T^3+O(T^4),T,4), series(-1*T+(54119/1440-1591/1440*alpha)*T^2+(-41285/36+27007...
[[series(1/2+(-54119/2880+1591/2880*alpha)*T+(138391/224-26189/1440*alpha)*T^2+(-8270626649/453600+486929033/907200*alpha)*T^3+O(T^4),T,4), series(-1*T+(54119/1440-1591/1440*alpha)*T^2+(-41285/36+27007...
[[series(1/2+(-54119/2880+1591/2880*alpha)*T+(138391/224-26189/1440*alpha)*T^2+(-8270626649/453600+486929033/907200*alpha)*T^3+O(T^4),T,4), series(-1*T+(54119/1440-1591/1440*alpha)*T^2+(-41285/36+27007...

The interpretation of this result is as follows: at alpha , the differential equation has a vector space of dimension 4 of solutions, which is the direct sum of a subspace of analytic solutions of dimension 3 and a "line" of singular solutions, generated by a solution L(z) = sqrt(alpha-z)*(1+O(z-alpha)) . Thus A(z) = lambda[A]*L(z)+g[A](z) , where g[A](z)  is analytic in the neighborhood of alpha  and similarly B(z) = lambda[B]*L(z)+g[B](z) . Now, singularity analysis tells us that the coefficients a[n]  behave asymptotically like

>    equivalent(lambda[A]*sqrt(alpha-z),z,n);

-1/2*1/Pi^(1/2)*lambda[A]*alpha^(1/2)*(1/n)^(3/2)*(34-alpha)^(-ln(exp(-n)))+O((1/n)^(5/2)*(34-alpha)^n)

and similarly for b[n]  with lambda[B]  in place of lambda[A] . Now, we deduce that lim( b[n] / a[n] )= zeta(3) = lambda[B] / lambda[A]  and consequently C(z) = A(z)*zeta(3)-B(z)  is analytic at alpha , as was to be proved.

5. 0 < zeta(3)-b[n]/a[n]

The proof is obtained by writing this difference as the infinite sum Sum(b[k]/a[k]-b[k-1]/a[k-1],k = n+1 .. infinity)

A recurrence satisfied by the numerator of the summand is readily found using gfun:

>    gfun[poltorec](A(k)*B(k+1)-A(k+1)*B(k),[subs(n=k,rec),subs(A=B,n=k,rec)],[A(k),B(k)],u(k));

(-k^3-3*k^2-3*k-1)*u(k)+(8+12*k+6*k^2+k^3)*u(k+1)

>    rsolve(%,u(k));

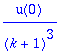
1/(k+1)^3*u(0)

and thus this is a sum of positive terms since 0 < a[k]  and the initial condition is positive:

>    value(subs(n=0,a[n])*subs(n=1,b[n])-subs(n=1,a[n])*subs(n=0,b[n]));

6

6. Conclusion

It is classical that the sequence d[n] =lcm(1,..., n ) grows asymptotically like e^n . This worksheet has thus proved that the sequence S[n] = d[n]^3*(a[n]*zeta(3)-b[n])  enjoys the following properties: it is positive and grows asymptotically like 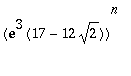(exp(3)*(17-12*sqrt(2)))^n .  Now, this tends to 0:

>    evalf(exp(3)*(17-12*sqrt(2)));

.5912631726

>   

If zeta(3)  were rational, then for n  large enough, d[n]^3*zeta(3)  would be an integer and the sequence S[n]  would be a sequence of positive integers tending to 0, which is impossible. This concludes the proof. Further refinements lead to irrationality measures.